PRML

永井 忠一 2020.4.19

多項式曲線フィッティング(Polynomial Curve Fitting)

\[ y(x,\mathbf{w}) = w_0 + w_1x + w_2x^2 + \cdots + w_Mx^M = \sum_{j=0}^{M}w_jx^j \]\( M \)は多項式の次数(order)、ベクトル\( \mathbf w \)は多項式の係数ベクトル

回帰問題(regression problem)

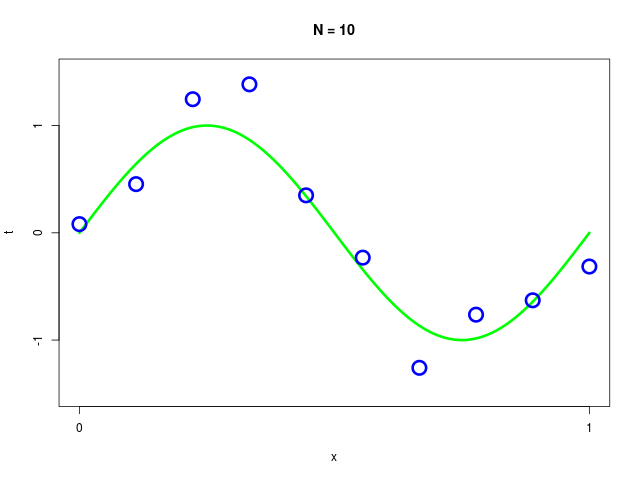
訓練データ集合(training data set)には、人工的に生成されたデータを使用

青○は \( N=10 \)個の訓練データ集合。緑の曲線は、データ生成に使った背後にある関数 \( \sin(2\pi x) \)

データを生成するプログラム

R言語
png("fig1.png", width=640, height=480)

x <- seq(0, 1, length=1024)
t <- sin(2*pi*x)
N <- 10 # a training data set of 10 points
plot(x, t, ylim=c(-1.5, 1.5), main=paste("N =", N), xlab="x", ylab="t", xaxp=c(0, 1, 1), yaxp=c(-1, 1, 2), type="n")
lines(x, t, col="green", lwd=3.5)

x <- seq(0, 1, length=N)
set.seed(6) # adhoc
t <- sin(2*pi*x) + rnorm(N, 0, 0.3)
points(x, t, col="blue", lwd=3.5, cex=2.5)

dev.off()

write.table(data.frame(x=x, t=t), "dataset1.txt", row.names=FALSE, col.names=FALSE, sep="\t")

R言語と開発環境(ESS)のインストール（私の環境ではapt）

Linux
$ sudo apt install r-base elpa-ess

ESS(Emacs Speaks Statistics)は、パッケージ名が ess から elpa-ess に変更になる。パッケージを『$ apt-cache search ess』などして探す。詳細は、『$ apt show elpa-ess』や『$ apt show ess』など

最小二乗法

二乗和誤差\[ E(\mathbf{w}) = \frac{1}{2}\sum_{n=1}^N\{y(x_n,\mathbf{w}) - t_n\}^2 \]を最小化する

誤差関数 \( E(\mathbf w) \) を最小にする係数ベクトル \( \mathbf w \) を求める

\( \mathbf w \) の求め方\[ \frac{\partial E}{ \partial w_0} = \frac{\partial E}{ \partial w_1} = \cdots = \frac{\partial E}{ \partial w_M} = 0 \]を解く

２次式(\( M=2 \))の例。目的関数を書き下す\[ E(\mathbf w) = \frac{1}{2}\sum_{n}\{y(x_n,\mathbf{w}) - t_n\}^2 = \frac{1}{2}\sum_{n}(w_0 + w_1x_n + w_2x_n^2 - t_n)^2 \]

未知ベクトル \( \mathbf w \) で偏微分して \( 0 \) とおく\[ \begin{align} \frac{\partial E}{ \partial w_0} &= \frac{1}{2}\sum_{n}2(w_0 + w_1x_n + w_2x_n^2 - t_n) = \sum_{n}(w_0 + w_1x_n + w_2x_n^2 - t_n) = \left( \sum_n 1 \right)w_0 + \left( \sum_n x_n \right)w_1 + \left( \sum_n x_n^2 \right)w_2 - \sum_n t_n = 0 \\ ~~~ \frac{\partial E}{ \partial w_1} &= \frac{1}{2}\sum_{n}2x_n(w_0 + w_1x_n + w_2x_n^2 - t_n) = \sum_{n}x_n(w_0 + w_1x_n + w_2x_n^2 - t_n) = \left( \sum_n x_n \right)w_0 + \left( \sum_n x_n^2 \right)w_1 + \left( \sum_n x_n^3 \right)w_2 - \sum_n x_nt_n = 0 ~~~ \\ ~~~ \frac{\partial E}{ \partial w_2} &= \frac{1}{2}\sum_{n}2x_n^2(w_0 + w_1x_n + w_2x_n^2 - t_n) = \sum_{n}x_n^2(w_0 + w_1x_n + w_2x_n^2 - t_n) = \left( \sum_n x_n^2 \right)w_0 + \left( \sum_n x_n^3 \right)w_1 + \left( \sum_n x_n^4 \right)w_2 - \sum_n x_n^2t_n = 0 ~~~ \end{align} \]

行列の形で整理する\[ \begin{align} \begin{pmatrix} \sum_n 1 & \sum_n x_n & \sum_n x_n^2 \\ \sum_n x_n & \sum_n x_n^2 & \sum_n x_n^3 \\ \sum_n x_n^2 & \sum_n x_n^3 & \sum_n x_n^4 \end{pmatrix}\begin{pmatrix} w_0 \\ w_1 \\ w_2 \end{pmatrix} - \begin{pmatrix} \sum_n t_n \\ \sum_n x_nt_n \\ \sum_n x_n^2t_n \end{pmatrix} &= \mathbf 0 \\ \begin{pmatrix} \sum_n 1 & \sum_n x_n & \sum_n x_n^2 \\ \sum_n x_n & \sum_n x_n^2 & \sum_n x_n^3 \\ \sum_n x_n^2 & \sum_n x_n^3 & \sum_n x_n^4 \end{pmatrix}\begin{pmatrix} w_0 \\ w_1 \\ w_2 \end{pmatrix} &= \begin{pmatrix} \sum_n t_n \\ \sum_n x_nt_n \\ \sum_n x_n^2t_n \end{pmatrix} \\ \begin{pmatrix} w_0 \\ w_1 \\ w_2 \end{pmatrix} &= \begin{pmatrix} \sum_n 1 & \sum_n x_n & \sum_n x_n^2 \\ \sum_n x_n & \sum_n x_n^2 & \sum_n x_n^3 \\ \sum_n x_n^2 & \sum_n x_n^3 & \sum_n x_n^4 \end{pmatrix}^{-1}\begin{pmatrix} \sum_n t_n \\ \sum_n x_nt_n \\ \sum_n x_n^2t_n \end{pmatrix} \end{align} \]

\( M \) 次式の場合（一般解）\[ \begin{align} \mathbf{A}\mathbf{w} &= \mathbf b \\ \mathbf{w} &= \mathbf{A}^{-1}\mathbf b \end{align} \]ただし、\[ A_{ij} = \sum_n x_n^{i+j},\ b_i = \sum_n x_n^i t_n \] \[ (i,j = 0, \ldots, M) \]行列・ベクトルの定義\[ \mathbf A \equiv \begin{pmatrix} \sum_n x_n^{0+0} & \cdots & \sum_n x_n^{0+M} \\ \vdots & \ddots & \vdots \\ \sum_n x_n^{M+0} & \cdots & \sum_n x_n^{M+M} \end{pmatrix},\ \mathbf b \equiv \begin{pmatrix} \sum_n x_n^0 t_n \\ \vdots \\ \sum_n x_n^M t_n \end{pmatrix},\ \mathbf w \equiv \begin{pmatrix} w_0 \\ \vdots \\ w_M \end{pmatrix} \]

過学習(over-fitting)

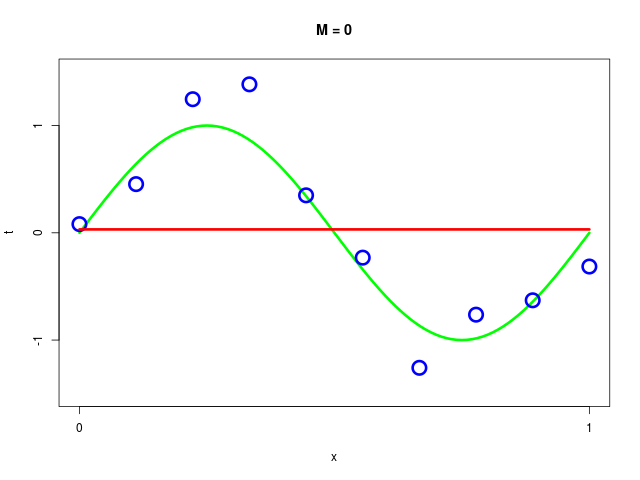
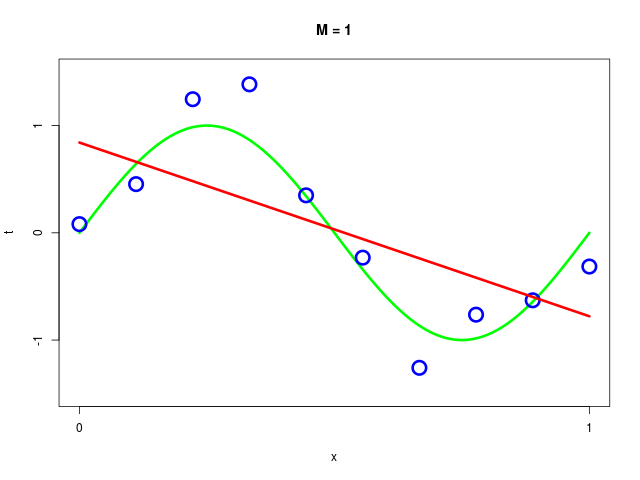
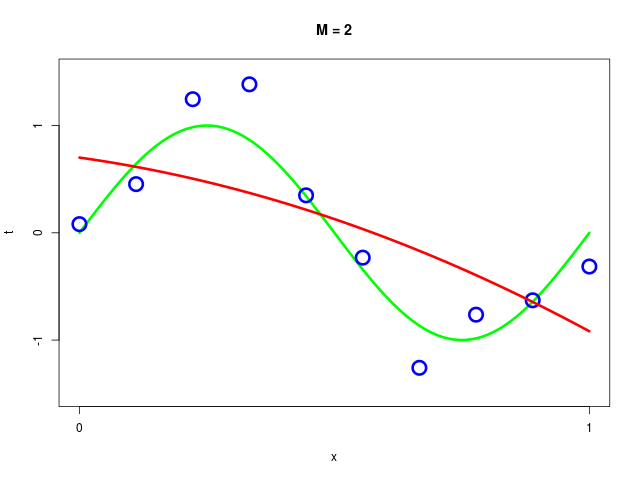
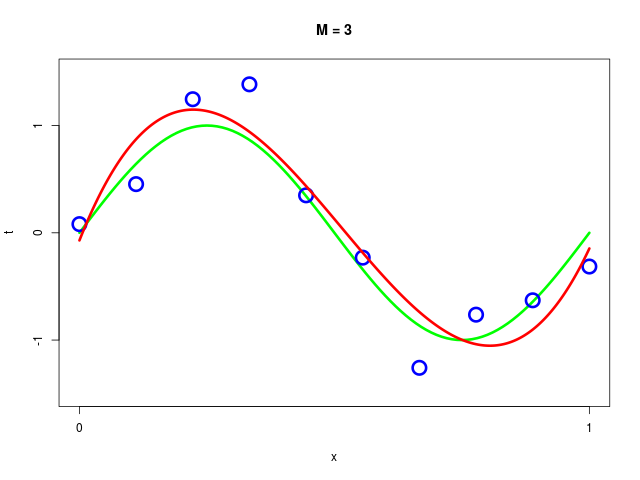
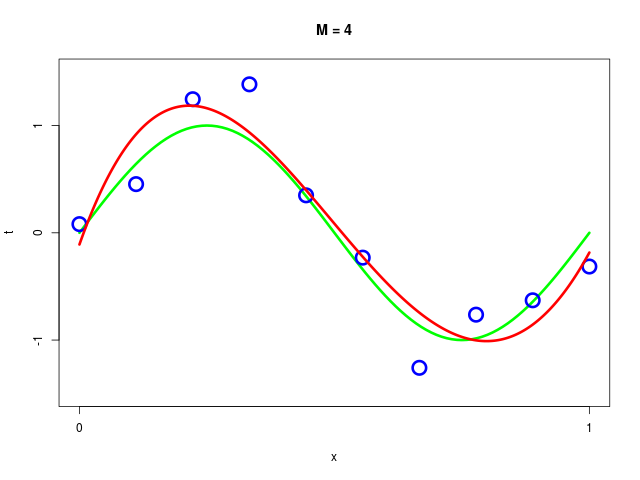
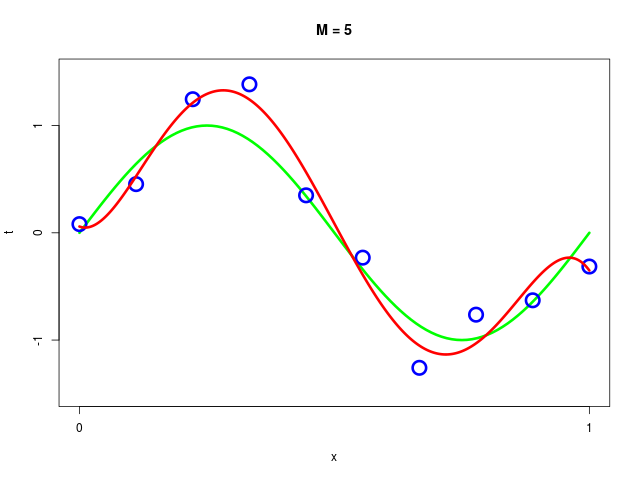
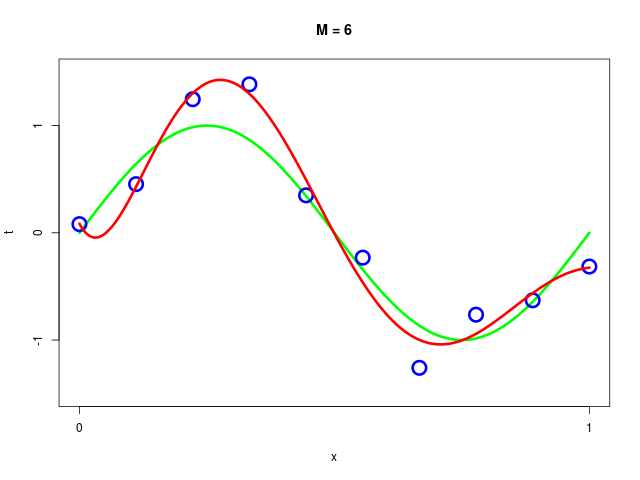
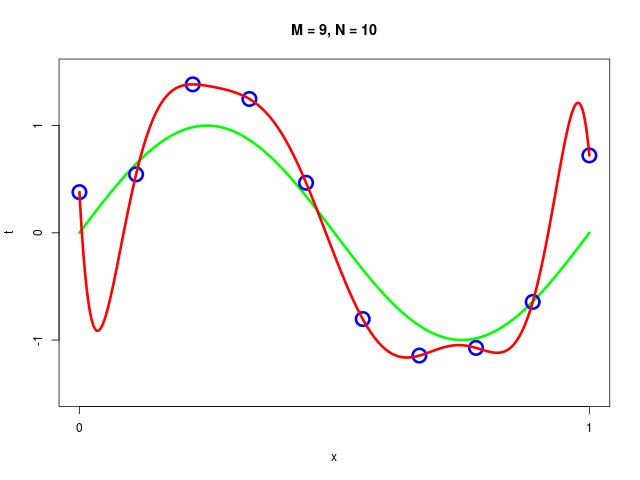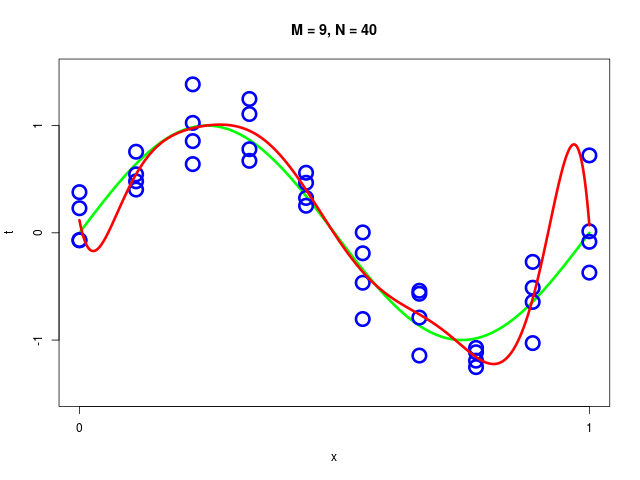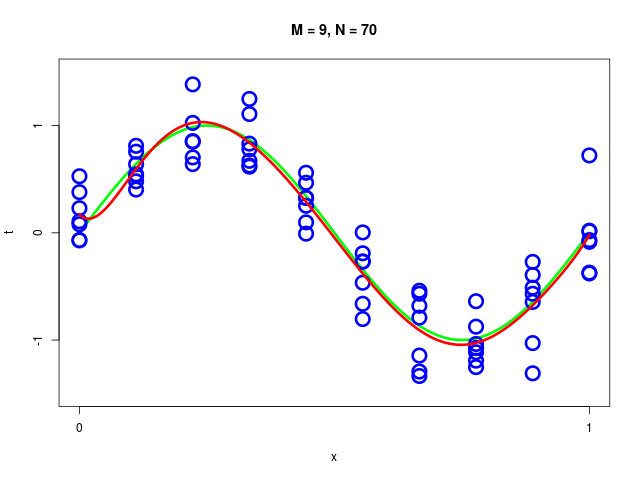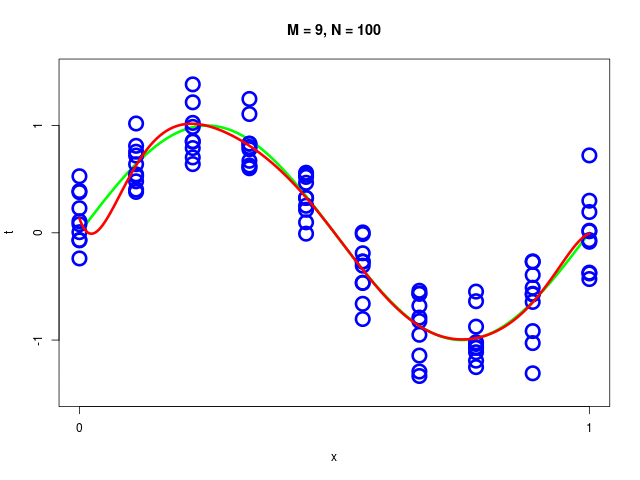
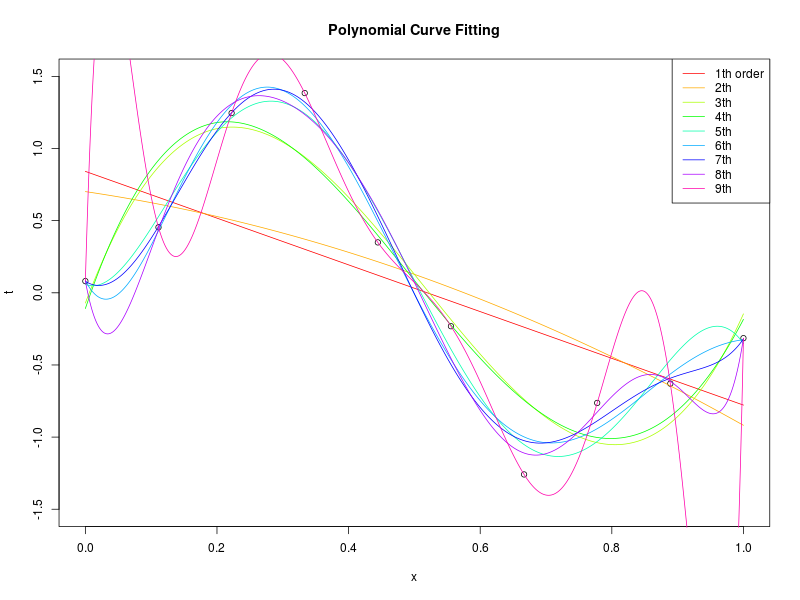
データ集合に次数 \( M = 1, 2, \ldots , 9\) を持つ多項式をフィッティングした結果

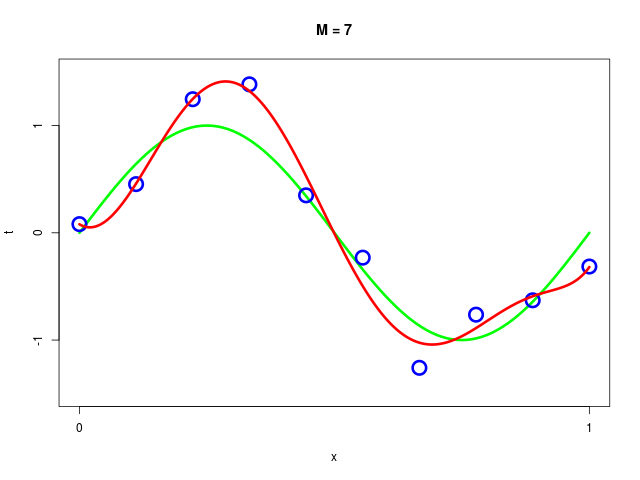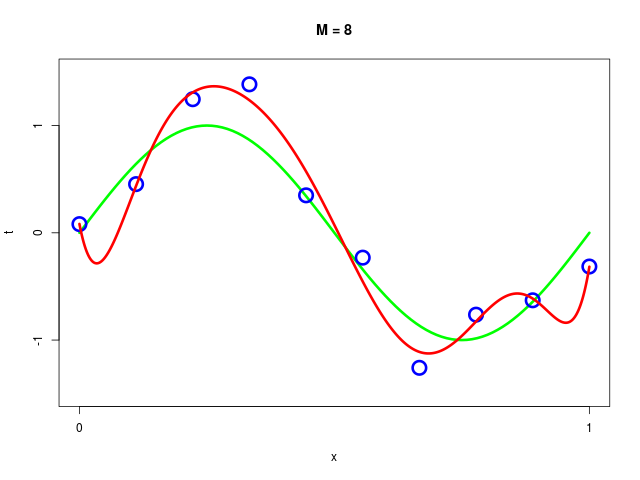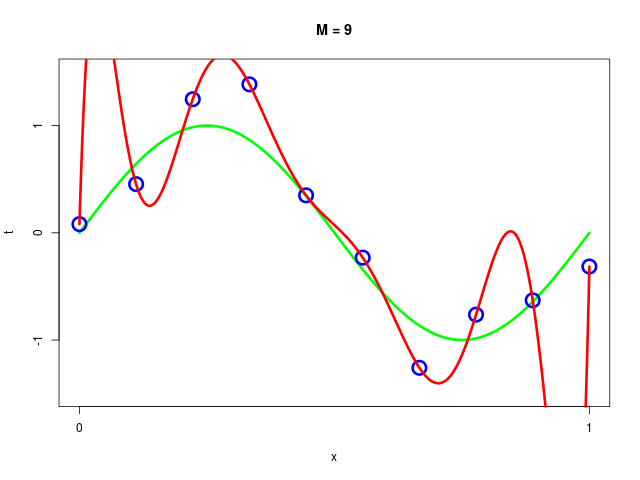得られた解 \( \mathbf{w^*} \) の値を確認

係数ベクトル
\( w^*_0 \)\( w^*_1 \)\( w^*_2 \)\( w^*_3 \)\( w^*_4 \)\( w^*_5 \)\( w^*_6 \)\( w^*_7 \)\( w^*_8 \)\( w^*_9 \)
\( M=0 \) 0.03
\( M=1 \) 0.84 -1.62
\( M=2 \) 0.70 -0.67 -0.95
\( M=3 \)-0.07 12.04 -34.46 22.34
\( M=4 \)-0.11 13.47 -41.66 33.90 -5.78
\( M=5 \) 0.06 -1.79 85.53 -325.65 406.34 -164.85
\( M=6 \) 0.09 -8.90 173.27 -703.27 1136.08 -813.97 216.37
\( M=7 \) 0.08 -2.85 73.40 -111.04 -538.48 1628.03 -1555.80 506.34
\( M=8 \) 0.08-24.81 516.20-3450.90 12060.96-24602.79 29046.84-18229.98 4684.08
\( M=9 \) 0.08159.24-3734.9634841.09-167830.87465492.35-773458.81760154.62-407139.8891516.81

プログラム

R言語
get.A <- function(x, t, M) {
    A <- matrix(0, nrow=M+1, ncol=M+1)
    for (i in 0:M)
        for (j in 0:M)
            A[i+1,j+1] <- sum(x^(i+j))
    return(A)
}

get.b <- function(x, t, M) {
    b <- rep(0, M+1)
    for (i in 0:M)
        b[i+1] <- sum((x^i)*t)
    return(b)
}

y <- function(x, w, M) { # assert(M == length(w) - 1)
    retval <- 0
    for (i in 0:M)
        retval <- retval + w[i+1]*x^i
    return(retval)
}

visualize <- function(X, t, w, M) { # assert(M == length(w) - 1)
    png(paste("fig2-", M+1, ".png", sep=""), width=640, height=480)
    plot(X, t, ylim=c(-1.5, 1.5), main=paste("M =", M), xlab="x", ylab="t", xaxp=c(0, 1, 1), yaxp=c(-1, 1, 2), type="n")
    x <- seq(0, 1, len=1024)
    curve(sin(2*pi*x), col="green", lwd=3.5, add=TRUE)
    points(X, t, col="blue", lwd=3.5, cex=2.5)
    lines(x, sapply(x, function(x) y(x, w, M)), col="red", lwd=3.5)
    dev.off()
}

dataset <- read.table("dataset1.txt"); colnames(dataset) <- c("x", "t")

for (order in 0:9) {
    A <- get.A(dataset$x, dataset$t, order)
    b <- get.b(dataset$x, dataset$t, order)
    w <- solve(A, b)
    visualize(dataset$x, dataset$t, w, order)
    if (FALSE) { # show coefficients
        #print(paste("M =", order))
        print(round(w, 2))
    }
}

データ集合のサイズ

特定のモデルの、データ集合のサイズが変化したときの振る舞い

プログラム
R言語
get.A <- function(x, t, M) {
    A <- matrix(0, nrow=M+1, ncol=M+1)
    for (i in 0:M)
        for (j in 0:M)
            A[i+1,j+1] <- sum(x^(i+j))
    return(A)
}

get.b <- function(x, t, M) {
    b <- rep(0, M+1)
    for (i in 0:M)
        b[i+1] <- sum((x^i)*t)
    return(b)
}

y <- function(x, w, M) { # assert(M == length(w) - 1)
    retval <- 0
    for (i in 0:M)
        retval <- retval + w[i+1]*x^i
    return(retval)
}

y <- function(x, w) {
    M <- length(w) - 1
    retval <- 0
    for (i in 0:M) # Mth order
        retval <- retval + w[i+1]*x^i # polynomial
    return(retval)
}

g_sequence <- 0
visualize <- function(fig, X, t, w, N) {
    M <- length(w) - 1
    png(paste(paste(fig, "-", sep=""), formatC(g_sequence, width=2, flag="0"), ".png", sep=""), width=640, height=480)
    g_sequence <<- g_sequence + 1
    plot(X, t, ylim=c(-1.5, 1.5), main=paste(paste("M =", M), paste("N =", N), sep=", "), xlab="x", ylab="t", xaxp=c(0, 1, 1), yaxp=c(-1, 1, 2), type="n")
    x <- seq(0, 1, len=1024)
    curve(sin(2*pi*x), col="green", lwd=3.5, add=TRUE)
    points(X, t, col="blue", lwd=3.5, cex=2.5)
    lines(x, sapply(x, function(x) y(x, w)), col="red", lwd=3.5)
    dev.off()
}

generate.dataset <- function(N) {
    x <- seq(0, 1, length=N)
    t <- sin(2*pi*x) + rnorm(N, 0, 0.3)
    return(data.frame(x=x, t=t))
}

order <- 9 # th order

for (size in seq(10, 100, by=5)) { # size of data set
    set.seed(6) # adhoc
    dataset <- generate.dataset(size)
    A <- get.A(dataset$x, dataset$t, order)
    b <- get.b(dataset$x, dataset$t, order)
    w <- solve(A, b)
    visualize("fig3", dataset$x, dataset$t, w, size)
}

for (i in 1:10) { # other way
    set.seed(0) # adhoc
    for (j in 1:i) {
        if (j == 1)
            dataset <- generate.dataset(10)
        else
            dataset <- merge(dataset, generate.dataset(10), all=TRUE)
    }
    A <- get.A(dataset$x, dataset$t, order)
    b <- get.b(dataset$x, dataset$t, order)
    w <- solve(A, b)
    visualize("fig4", dataset$x, dataset$t, w, 10*i)
}

if (FALSE) { # make animation
    system("convert -delay 100 -loop 0 fig3-*.png fig3.gif")
    system("convert -delay 100 -loop 0 fig4-*.png fig4.gif")
}

グラフツールやライブラリの利用

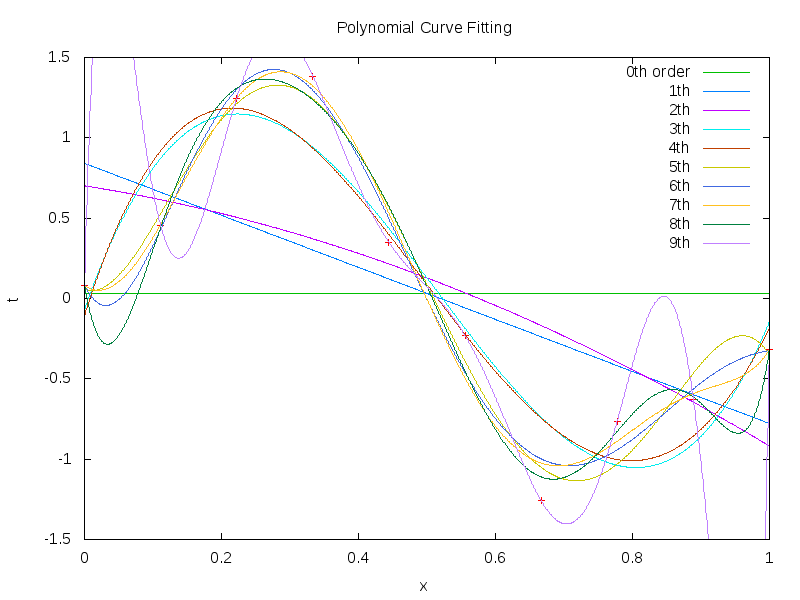
gnuplotのfitコマンド

コマンドと推定された係数（係数は３次の例）
gnuplot
set terminal png size 800,600
set output "fig5.png"

f0(x) = w00
f1(x) = w10 + w11*x
f2(x) = w20 + w21*x + w22*x**2
f3(x) = w30 + w31*x + w32*x**2 + w33*x**3
f4(x) = w40 + w41*x + w42*x**2 + w43*x**3 + w44*x**4
f5(x) = w50 + w51*x + w52*x**2 + w53*x**3 + w54*x**4 + w55*x**5
f6(x) = w60 + w61*x + w62*x**2 + w63*x**3 + w64*x**4 + w65*x**5 + w66*x**6
f7(x) = w70 + w71*x + w72*x**2 + w73*x**3 + w74*x**4 + w75*x**5 + w76*x**6 + w77*x**7
f8(x) = w80 + w81*x + w82*x**2 + w83*x**3 + w84*x**4 + w85*x**5 + w86*x**6 + w87*x**7 + w88*x**8
f9(x) = w90 + w91*x + w92*x**2 + w93*x**3 + w94*x**4 + w95*x**5 + w96*x**6 + w97*x**7 + w98*x**8 + w99*x**9

dataset = "dataset1.txt"

fit f0(x) dataset via w00
fit f1(x) dataset via w10,w11
fit f2(x) dataset via w20,w21,w22
fit f3(x) dataset via w30,w31,w32,w33
fit f4(x) dataset via w40,w41,w42,w43,w44
fit f5(x) dataset via w50,w51,w52,w53,w54,w55
fit f6(x) dataset via w60,w61,w62,w63,w64,w65,w66
fit f7(x) dataset via w70,w71,w72,w73,w74,w75,w76,w77
fit f8(x) dataset via w80,w81,w82,w83,w84,w85,w86,w87,w88
fit f9(x) dataset via w90,w91,w92,w93,w94,w95,w96,w97,w98,w99

set title "Polynomial Curve Fitting"
set xlabel "x"
set ylabel "t"
set yrange [-1.5:1.5]

set sample 1024

plot dataset notitle, f0(x) title "0th order",\
     f1(x) title "1th", f2(x) title "2th", f3(x) title "3th", f4(x) title "4th", f5(x) title "5th", f6(x) title "6th", f7(x) title "7th", f8(x) title "8th", f9(x) title "9th"


FIT:    data read from "dataset1.txt"
        format = z
        #datapoints = 10
        residuals are weighted equally (unit weight)

function used for fitting: f3(x)
fitted parameters initialized with current variable values



 Iteration 0
 WSSR        : 0.862599          delta(WSSR)/WSSR   : 0
 delta(WSSR) : 0                 limit for stopping : 1e-05
 lambda	  : 0.665142

initial set of free parameter values

w30             = -0.07092
w31             = 12.0406
w32             = -34.4561
w33             = 22.3404

After 1 iterations the fit converged.
final sum of squares of residuals : 0.862599
rel. change during last iteration : -1.41577e-15

degrees of freedom    (FIT_NDF)                        : 6
rms of residuals      (FIT_STDFIT) = sqrt(WSSR/ndf)    : 0.379165
variance of residuals (reduced chisquare) = WSSR/ndf   : 0.143766

Final set of parameters            Asymptotic Standard Error
=======================            ==========================

w30             = -0.07092         +/- 0.3441       (485.2%)
w31             = 12.0406          +/- 3.153        (26.18%)
w32             = -34.4561         +/- 7.579        (22%)
w33             = 22.3404          +/- 4.973        (22.26%)


correlation matrix of the fit parameters:

               w30    w31    w32    w33    
w30             1.000 
w31            -0.758  1.000 
w32             0.593 -0.959  1.000 
w33            -0.500  0.898 -0.984  1.000

R言語のlm(), poly(), predict()関数

プログラムと推定された係数の確認（係数は３次の例）
R言語
dataset <- read.table("dataset1.txt"); colnames(dataset) <- c("x", "t")

# fit0 = ?!?
fit1 <- lm(t ~ poly(x, degree=1, raw=TRUE), data=dataset)
fit2 <- lm(t ~ poly(x, degree=2, raw=TRUE), data=dataset)
fit3 <- lm(t ~ poly(x, degree=3, raw=TRUE), data=dataset)
fit4 <- lm(t ~ poly(x, degree=4, raw=TRUE), data=dataset)
fit5 <- lm(t ~ poly(x, degree=5, raw=TRUE), data=dataset)
fit6 <- lm(t ~ poly(x, degree=6, raw=TRUE), data=dataset)
fit7 <- lm(t ~ poly(x, degree=7, raw=TRUE), data=dataset)
fit8 <- lm(t ~ poly(x, degree=8, raw=TRUE), data=dataset)
fit9 <- lm(t ~ poly(x, degree=9, raw=TRUE), data=dataset)

png("fig6.png", width=800, height=600)
plot(dataset$x, dataset$t, main="Polynomial Curve Fitting", xlab="x", ylab="t", ylim=c(-1.5, 1.5))
x <- seq(0, 1, len=1024)
lines(x, predict(fit1, newdata=data.frame(X=x)), col=rainbow(9)[1])
lines(x, predict(fit2, newdata=data.frame(X=x)), col=rainbow(9)[2])
lines(x, predict(fit3, newdata=data.frame(X=x)), col=rainbow(9)[3])
lines(x, predict(fit4, newdata=data.frame(X=x)), col=rainbow(9)[4])
lines(x, predict(fit5, newdata=data.frame(X=x)), col=rainbow(9)[5])
lines(x, predict(fit6, newdata=data.frame(X=x)), col=rainbow(9)[6])
lines(x, predict(fit7, newdata=data.frame(X=x)), col=rainbow(9)[7])
lines(x, predict(fit8, newdata=data.frame(X=x)), col=rainbow(9)[8])
lines(x, predict(fit9, newdata=data.frame(X=x)), col=rainbow(9)[9])
legend("topright", legend=c("1th order", "2th", "3th", "4th", "5th", "6th", "7th", "8th", "9th"), col=rainbow(9), lty=c(1))
dev.off()
> summary(fit3)

Call:
lm(formula = t ~ poly(x, degree = 3, raw = TRUE), data = dataset)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.52050 -0.14795  0.02551  0.24273  0.44259 

Coefficients:
                                  Estimate Std. Error t value Pr(>|t|)   
(Intercept)                       -0.07092    0.34414  -0.206  0.84354   
poly(x, degree = 3, raw = TRUE)1  12.04065    3.15276   3.819  0.00877 **
poly(x, degree = 3, raw = TRUE)2 -34.45612    7.57902  -4.546  0.00391 **
poly(x, degree = 3, raw = TRUE)3  22.34035    4.97349   4.492  0.00414 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.3792 on 6 degrees of freedom
Multiple R-squared:  0.8674,	Adjusted R-squared:  0.8012 
F-statistic: 13.09 on 3 and 6 DF,  p-value: 0.004835

確率論(Probability Theory)

確率の基本的な法則

加法則(sum rule) \[ ~ p(X)=\sum_Y p(X, Y) \]
乗法則(product rule) \[ ~ p(X,Y)=p(Y|X)p(X) \]
の２つ

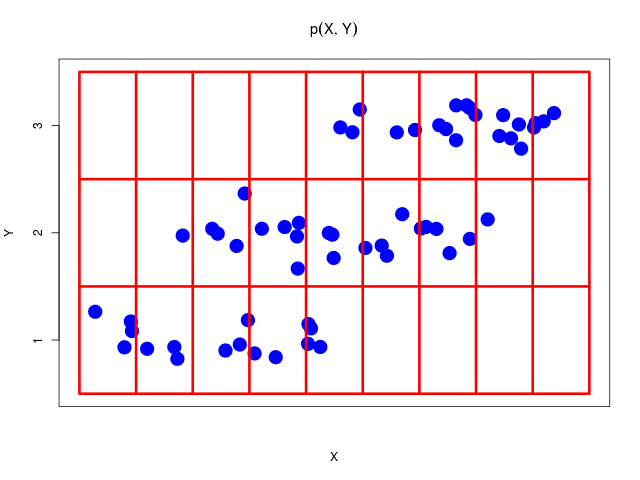
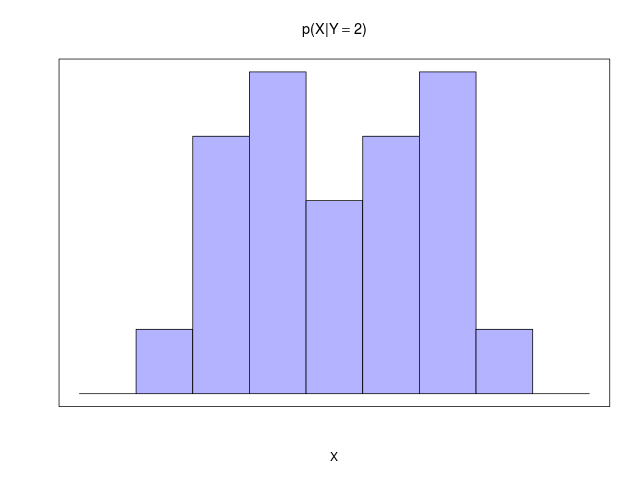
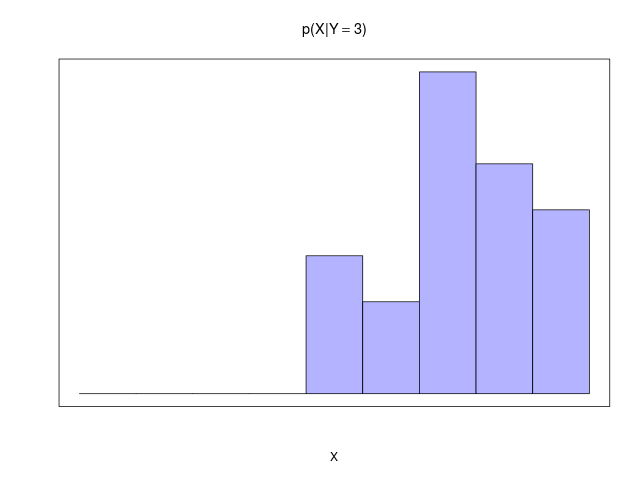
２つの確率変数\( X, Y \)を考える。\( X \)の値は\( \{x_i\}(i = 1,\ldots,M) \) 、\( Y \)の値は\( \{ y_j \}(j = 1,\ldots,L) \)の値をとる。総数\( N \)回の試行のうち、\( X = x_i\)かつ\( Y = y_j \)となる回数を\( n_{ij} \)、\( X = x_i \)となる回数を\( c_i \)、\( Y = y_j \)となる回数を\( r_j \)とする

同時確率(joint probability)\[ p(X=x_i, Y=y_j) = \frac{n_{ij}}{N} \]

周辺確率(marginal probability)

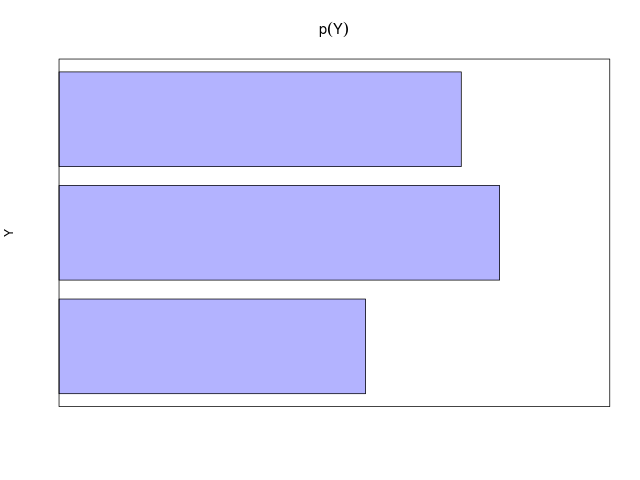
（\( Y \)について和をとり、周辺化した場合） 
\[ ~ p(X=x_i) = \frac{c_i}{N} = \sum_{j=1}^{L}p(X=x_i, Y=y_j) \]
（\( X \)について和をとり、周辺化した場合） 
\[ ~ p(Y=y_j) = \frac{r_j}{N} = \sum_{i=1}^{M}p(X=x_i, Y=y_j) \]
これ（↑）が確率の加法定理

条件付き確率(conditional probability)

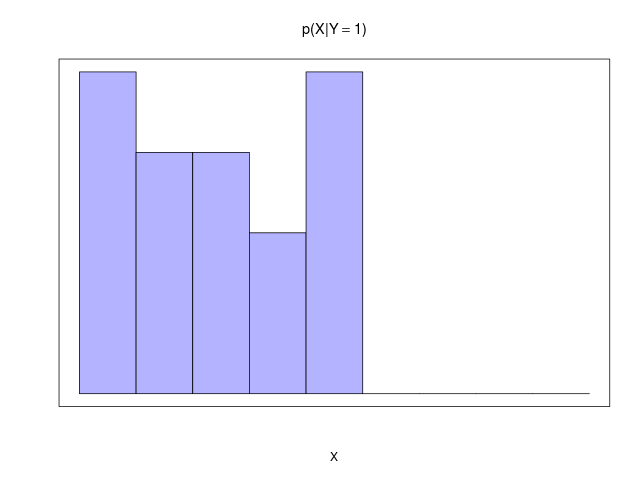
\( X = x_i \)が与えられた\( Y = y_j \)の条件付き確率 
\[ ~ p(Y=y_j | X=x_i) = \frac{n_{ij}}{c_i} \]
\( Y = y_j \)が与えられた\( X = x_i \)の条件付き確率 
\[ ~ p(X=x_i | Y=y_j ) = \frac{n_{ij}}{r_j} \]

上記の\( p(X=x_i, Y=y_j) = n_{ij}/N \)、\( p(X=x_i) = c_i/N \)および上式\( p(Y=y_j | X=x_i) = n_{ij}/c_i \)より\[ p(X=x_i, Y=y_j) = \frac{n_{ij}}{N} = \frac{n_{ij}}{c_i} \cdot \frac{c_i}{N} = p(Y=y_j | X=x_i)p(X=x_i) \]となる。これ（↑）が確率の乗法定理

確率変数\( X \)が値\( x_i \)をとる確率が\( p(X=x_i) \)。文脈上明らかなとき、確率変数\( X \)上の確率分布を\( p(X) \)、その分布が値\( x_i \)をとる確率を\( p(x_i) \)と簡易表記

同時分布、周辺分布および条件付き分布の例

２変数の同時分布（\( N = 60 \)個）による、周辺分布および条件付き分布の概念（図示）

ソースコード

R言語
set.seed(0)
tmp <-as.integer(runif(60, 0, 3))
i <- sum(tmp == 0)
j <- sum(tmp == 1)
k <- 60 - (i + j) # adhoc
set.seed(0) # adhoc
x <- c(runif(i, 0, 4.5), runif(j, 1.75, 7.25), runif(k, 4.5, 9))
y <- c(rnorm(i, 1, 0.15), rnorm(j, 2, 0.15), rnorm(k, 3, 0.15))

png("fig7.png", width=640, height=480)
plot(x, y, xlim=c(0, 9), ylim=c(0.5, 3.5), main=expression(p(X,Y)), xlab="X", ylab="Y", xaxt="n", yaxp=c(1, 3, 2), pch=19, col="blue", cex=2.5)
lines(c(0, 9,  9,  0,  0), c(0.5, 0.5,  3.5,  3.5,  0.5), col="red", lwd=3.5) # box
for (i in c(1.5, 2.5)) # horizontal
    lines(c(0, 9), c(i, i), col="red", lwd=3.5)
for (i in 1:8) # vertical
    lines(c(i, i), c(0.5, 3.5), col="red", lwd=3.5)
dev.off()

my.histgram <- function(val) { # adhoc
    retval <- rep(0, max(round(val)))
    for (idx in round(val))
        retval[idx] <- retval[idx] + 1
    return(retval)
}

png("fig8.png", width=640, height=480)
barplot(my.histgram(y), xlim=c(0, (max(my.histgram(y))*1.25)), main=expression(p(Y)), ylab="Y", col="#B3B3FF", xaxt="n", yaxp=c(0, 3, 3), horiz=TRUE)
box()
dev.off()

png("fig9.png", width=640, height=480)
hist(x, main=expression(p(X)), xlab="X", ylab="", col="#B3B3FF", xaxt="n", yaxt="n", breaks=seq(0, 9))
box()
dev.off()

png("fig10.png", width=640, height=480)
hist(x[(0.5 <= y) & (y < 1.5)], xlim=c(0, 9), main=expression(paste(p, "(", X, "|", Y==1, ")")), xlab="X", ylab="", col="#B3B3FF", xaxt="n", yaxt="n", breaks=seq(0, 9))
box()
dev.off()

png("fig11.png", width=640, height=480)
hist(x[(1.5 <= y) & (y < 2.5)], xlim=c(0, 9), main=expression(paste(p, "(", X, "|", Y==2, ")")), xlab="X", ylab="", col="#B3B3FF", xaxt="n", yaxt="n", breaks=seq(0, 9))
box()
dev.off()

png("fig12.png", width=640, height=480)
hist(x[(2.5 <= y) & (y <= 3.5)], xlim=c(0, 9), main=expression(paste(p, "(", X, "|", Y==3, ")")), xlab="X", ylab="", col="#B3B3FF", xaxt="n", yaxt="n", breaks=seq(0, 9))
box()
dev.off()

ベイズの定理(Bayes' theorem)

乗法則の変形に過ぎないが、非常に有用な式変形の結果\[ p(Y | X) = \frac{p(X | Y)p(Y)}{p(X)} \]（実質、条件付き確率の定義）

辺々\( p(X) \)を掛けて、乗法定理から導ける\[ \begin{align} p(Y | X) &= \frac{p(X | Y)p(Y)}{p(X)} \\ p(Y | X)p(X) &= p(X | Y)p(Y) \\ p(X, Y) &= p(Y, X) \end{align} \]対称性(symmetry property)\( p(X,Y) = p(Y,X) \)より両辺は等しい

ベイズの定理の分母の\( p(X) \)を\( Y \)について和をとった形、周辺確率\( p(X) = \sum_Y p(X | Y)p(Y) \)とみなして\[ p(Y | X) = \frac{p(X | Y)p(Y)}{\sum_Y p(X | Y)p(Y)} \]この形で書かれることも多い

（\( p(X) \)を、加法定理を使い\( p(X) = \sum_Y p(X, Y) \)とし、さらに乗法定理を使って\( p(X) = \sum_Y p(X | Y)p(Y) \)と書き換え、\[ p(Y | X) = \frac{p(X | Y)p(Y)}{p(X)} = \frac{p(X | Y)p(Y)}{\sum_Y p(X | Y)p(Y)} \]と変形）

ベイズの定理の分母は、分子に表れる量（\( p(X | Y)p(Y) \)）で表すことができる。分母は、左辺の条件付確率をすべての\( Y \)について和をとったものが１になることを保証するための規格化（正規化）定数とみることができる（すべての事象の確率の和は１）

独立(independent)

２変数の同時分布が周辺分布の積に分解できるとき\[ p(X, Y) = p(X)p(Y) \]\( X \)と\( Y \)は独立であるという。独立であるならば、乗法定理から\[ p(X|Y) = p(X),\ p(Y|X) = p(Y) \]であることがわかる

期待値(expectation)と共分散(covariance)

期待値

重み付き平均(weighted average)
離散分布(discrete distribution)連続変数(continuous variable)
\[ \mathbb{E}[f] = \sum_x p(x)f(x) \]\[ \mathbb{E}[f] = \int p(x)f(x)\,\mathrm dx \]

多変数関数の期待値 \( \mathbb{E}[f] = \sum_{x,y}p(x,y)f(x,y) \)

どの変数について平均を取るのかを示すために添え字を使う

\( x \)について平均をとる例
離散分布連続変数
\[ \begin{align} \mathbb{E}_x[f] &= \\ \mathbb{E}_x[f(x,y)] &= \sum_x p(x)f(x,y) \end{align} \]\[ \begin{align} \mathbb{E}_x[f] &= \\ \mathbb{E}_x[f(x,y)] &= \int p(x)f(x,y)\,\mathrm dx \end{align} \]

\( \mathbb{E}_x[f(x,y)] \)は、関数\( f(x,y) \)の\( x \)の分布に関する平均を表す。期待値は\( y \)の関数になることに注意

条件付分布(conditional distribution)についての条件付き期待値(conditional expectation)

条件付き期待値
離散分布連続変数
\[ \mathbb{E}_x[f|y] = \sum_x p(x|y)f(x,y) \]\[ \mathbb{E}_x[f|y] = \int p(x|y)f(x,y)\,\mathrm dx \]

分散(variance)の定義\[ \mathrm{var}[f] = \mathbb{E}\left[ (f(x) - \mathbb{E}[f(x)]^2 \right] \]

（分散の公式）\[ \mathrm{var}[f] = \mathbb{E}[f(x)^2] - \mathbb{E}[f(x)]^2 \]と書くこともできる

変数\( x \)自体の分散を\[ \mathrm{var} = \mathbb{E}[x^2] - \mathbb{E}[x]^2 \]によって与えられると考えることができる（\( f(x) = x \)の意味）

２つの確率変数 \( x \) と \( y \) の共分散(covariance)の定義\[ \begin{align} \mathrm{cov}[x,y] &= \mathbb{E}_{x,y}\left[ \{x - \mathbb{E}[x]\}\{y - \mathbb{E}[y]\} \right] \\ &= \mathbb{E}_{x,y}[xy] - \mathbb{E}[x]\mathbb{E}[y] \end{align} \]もし \( x \) と \( y \) が独立なら共分散は \( 0 \) になる

確率変数 \( \mathbf{x} \) と \(\mathbf{y} \) の２つのベクトルの場合、共分散は行列\[ \begin{align} \mathrm{cov}[\mathbf{x},\mathbf{y}] &= \mathbb{E}_{\mathbf{x},\mathbf{y}}\left[ \{\mathbf{x} - \mathbb{E}[\mathbf{x}]\}\{\mathbf{y}^{\mathrm T} - \mathbb{E}[\mathbf{y}^{\mathrm T}]\} \right] \\ &= \mathbb{E}_{\mathbf{x},\mathbf{y}}[\mathbf{x}\mathbf{y}^{\mathrm T}] - \mathbb{E}[\mathbf{x}]\mathbb{E}[\mathbf{y}^{\mathrm T}] \end{align} \]ベクトル \( \mathbf x \) の成分間の共分散は、シンプルな表記 \( \mathrm{cov}[\mathbf{x}] \equiv \mathrm{cov}[\mathbf{x},\mathbf{x}] \) を使う

期待値の性質

\( x \)は確率変数、\( c \)が定数\[ \mathbb{E}[c] = c \]\[ \mathbb{E}[x + c] = \mathbb{E}[x] + c \]\[ \mathbb{E}[cx] = c\mathbb{E}[x] \]

\( x, y \)が確率変数\[ \mathbb{E}[x + y] = \mathbb{E}[x] + \mathbb{E}[y] \]

分散の性質

\( x \)は確率変数、\( c \)が定数\[ \mathrm{var}[c] = 0 \]\[ \mathrm{var}[x + c] = \mathrm{var}[x] \]\[ \mathrm{var}[cx] = c^2\mathrm{var}[x] \]

\( x, y \)は確率変数\[ \mathrm{var}[x + y] = \mathrm{var}[x] + \mathrm{var}[y] + 2\mathrm{cov}[x, y] \]\( x, y \)が独立ならば\[ \mathrm{var}[x + y] = \mathrm{var}[x] + \mathrm{var}[y] \]加法性が成り立つ（\(\ \mathrm{cov}[x, y] = 0 \) なので）

確率分布

例
ベルヌーイ分布二値離散パラメトリック(parametric)
二項分布
多項分布多値
ガウス分布１変数連続
多次元ガウス分布 多変数

多値変数(multinomial variable)

互いに排他なK個の状態の一つをとることができる離散変数

1-of-K表現(1-of-K coding scheme)

変数は、要素\( x_k \)の一つが\( 1 \)で、残りすべての要素が\( 0 \)の\( K \)次元ベクトル\( \mathbf{x} \)で表現される（→\( K \)種類の状態を表現）。たとえば、\( K = 6,\ x_3 = 1\)の場合（たとえば、サイコロの目の３が出た場合）\[ \mathbf{x} = (0, 0, 1, 0, 0, 0)^\mathrm{T} \]と表現される。このようなベクトル\( \mathbf{x} = (x_1, \ldots, x_K)^\mathrm{T} \)は\( \sum_{k=1}^K x_k = 1 \)を満たすことに注意

\( x_k = 1 \)となる確率をパラメータ\( \mu_k \)で表すと、\( \mathbf{x} \)の分布は\[ p(\mathbf{x}|\boldsymbol \mu) = \prod_{k=1}^{K} \mu_k^{x_k} = \begin{cases} \mu_1 & (x_1 = 1) \\ & \vdots \\ \mu_K & (x_K = 1) \end{cases} \]で与えられる

サイコロの例： 
\[ ~ p(\mathbf{x}|\boldsymbol \mu) = p\left((0,0,1,0,0,0)^\mathrm{T}|(\mu_1, \mu_2,\mu_3,\mu_4,\mu_5,\mu_6)^\mathrm{T}\right) = \mu_3 \]

ただし、\( \boldsymbol \mu = (\mu_1, \ldots, \mu_K)^\mathrm{T} \)は確率を表すので\[ \mu_k \geq 0,\ \sum_k \mu_k = 1 \]に拘束される

ガウス分布(Gaussian distribution)

正規分布(normal distribution)としても知られ、連続変数の分布に広く使用されているモデル

１変数の場合

\[ \mathcal{N}(x|\mu,\sigma^2) = \frac{1}{(2\pi\sigma^2)^{1/2}}\exp\left\{ -\frac{1}{2\sigma^2}(x - \mu)^2 \right\} \]

\( \mu \)：平均
\( \sigma^2 \)：分散
\( \sigma \)：標準偏差
\( \beta = 1/\sigma^2 \)：精度

確率密度の要件を満たす（\( x \) がどの値をとっても \( 0 \) より大きい（\( \exp \)なので）、積分は教科書など）\[ \mathcal{N}(x|\mu,\sigma^2) > 0,\ \int_{-\infty}^\infty \mathcal{N}(x|\mu,\sigma^2)\,\mathrm dx = 1 \]（確率密度が満たすべき条件\[ p(x) \geq 0,\ \int p(x)\,\mathrm dx = 1 \]\( p(x) \) は \( 0 \) 以上で、（関数が定義されている）全区間で積分すると \( 1 \)）

期待値と分散\[ \mathbb{E}[x] = \int_{-\infty}^\infty \mathcal{N}(x|\mu,\sigma^2)x\,\mathrm dx = \mu \]\[ \mathbb{E}[x^2] = \int_{-\infty}^\infty \mathcal{N}(x|\mu,\sigma^2)x^2\,\mathrm dx = \mu^2 + \sigma^2 \]\[ \mathrm{var}[x] = \mathbb{E}[x^2] - \mathbb{E}[x]^2 = \sigma^2 \]（計算は教科書など）

中心極限定理(central limit theorem)

ガウス分布は、複数の確率変数の和を考えているときにも生じる。（Laplaceによる）中心極限定理

\( N \) 個の一様分布から生成した乱数の平均のヒストグラム
実際、\( N \) の増加によるガウシアンへの収束は非常に速い

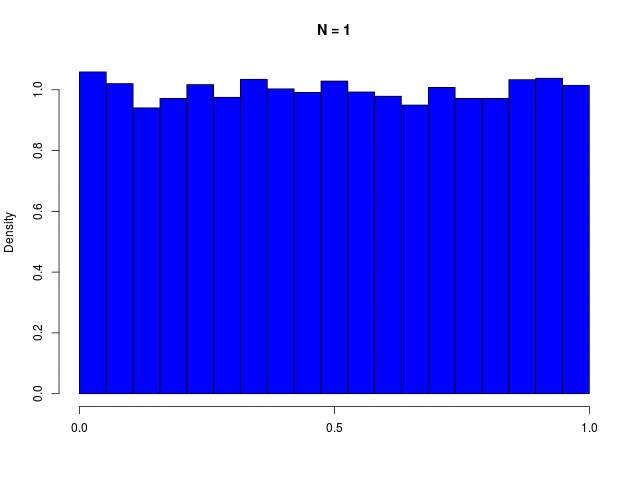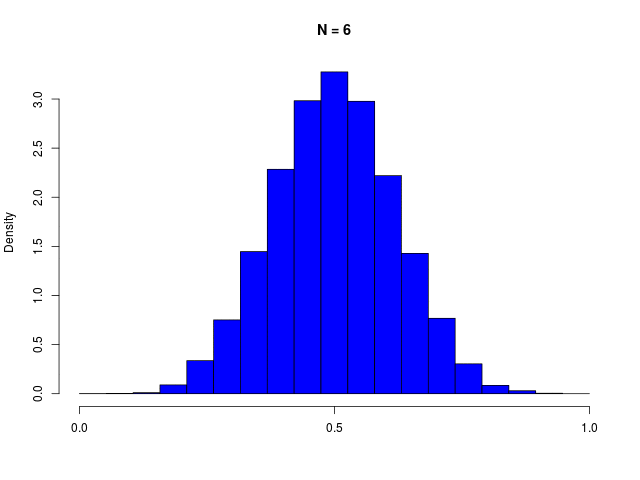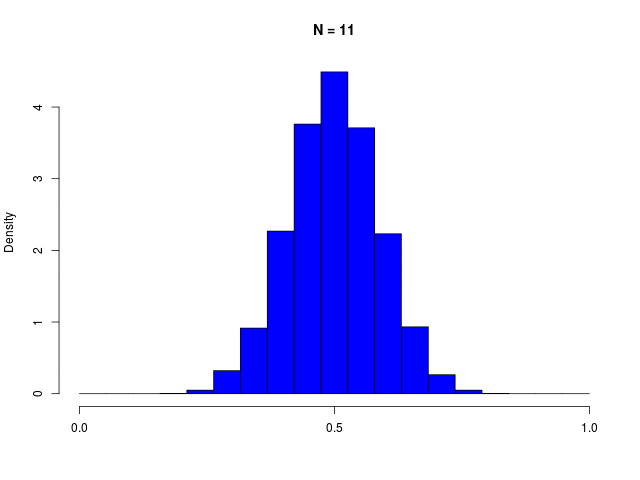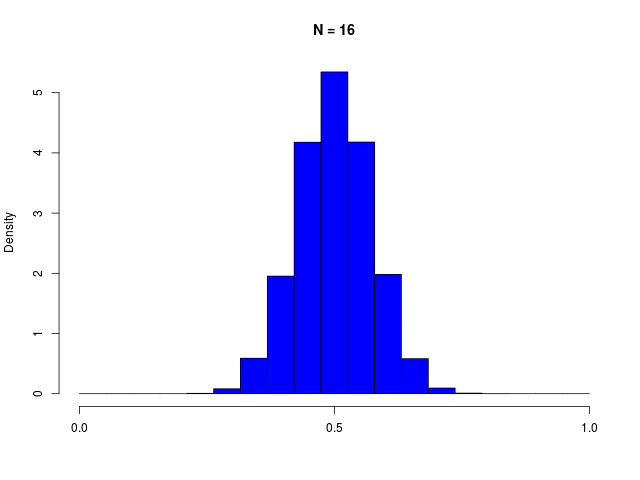シミュレーションのソースコード

R言語
set.seed(0)

samples <- 16*1024

for (N in 1:16) {
    val <- 0
    for (i in 1:N)
        val <- val + runif(samples)
    val <- val / N
    png(paste("fig13-", formatC(N, width=2, flag="0"), ".png", sep=""), width=640, height=480)
    hist(val, xlim=c(0, 1), main=paste("N =", N), breaks=seq(0, 1, len=20), xaxp=c(0, 1, 2), xlab="", col="blue", freq=FALSE)
    dev.off()
}

if (FALSE) # animation
    system("convert -delay 100 -loop 0 fig13-*.png fig13.gif")

二値確率変数の \( N \) 個の和で定義される \( m \) の分布である、二項分布(binomial distribution)は、\( N \to \infty \) でガウシアンに従う

乱数によるシミュレーションと確率密度関数のプロット

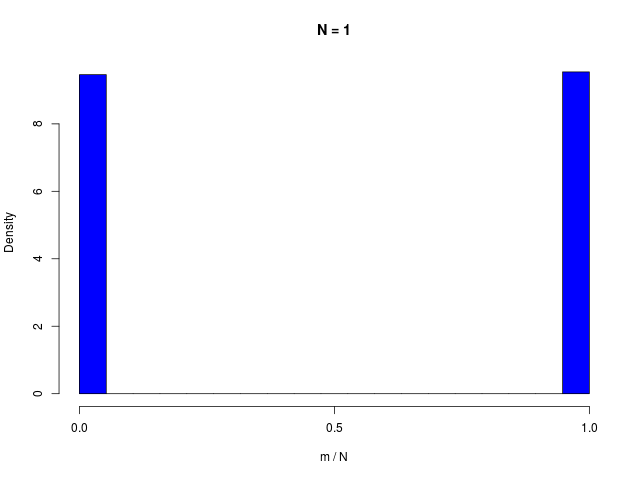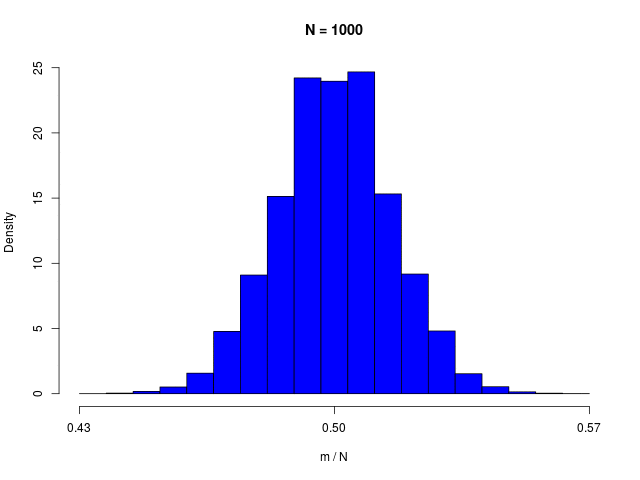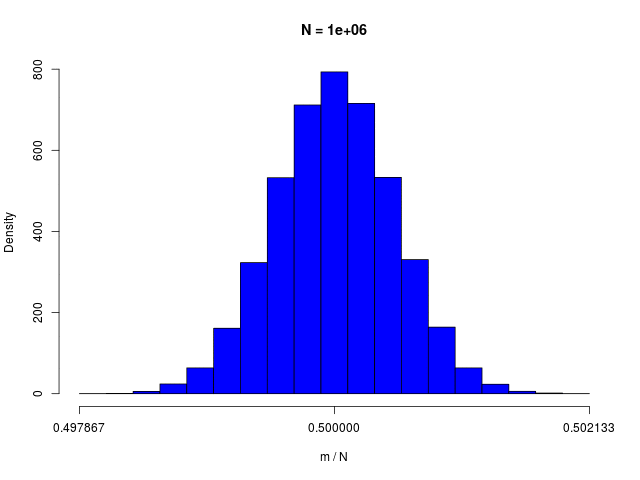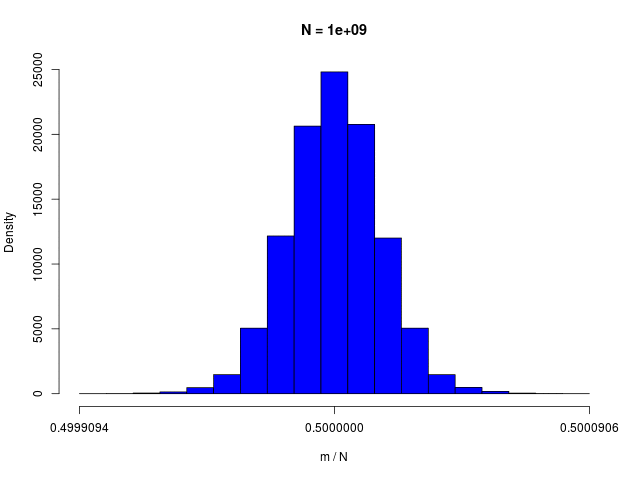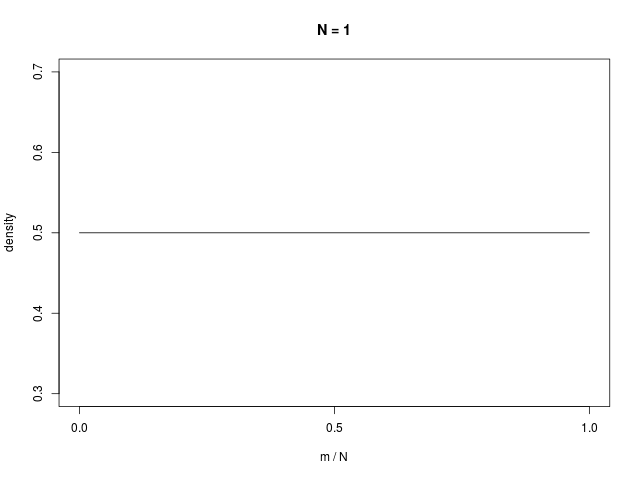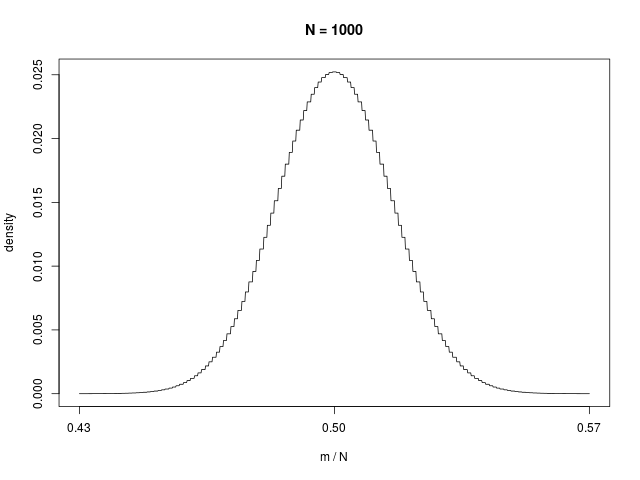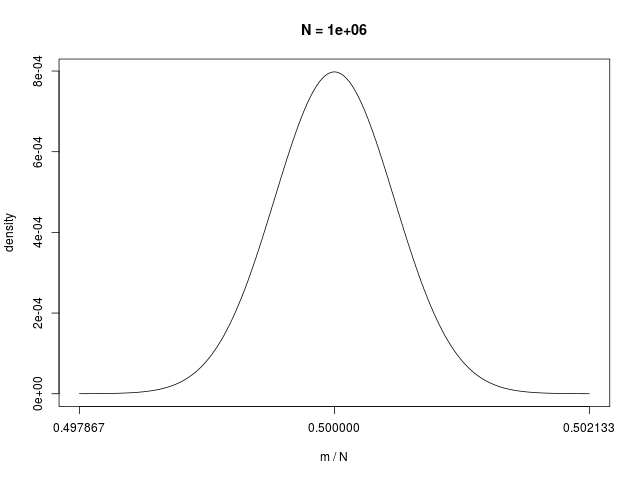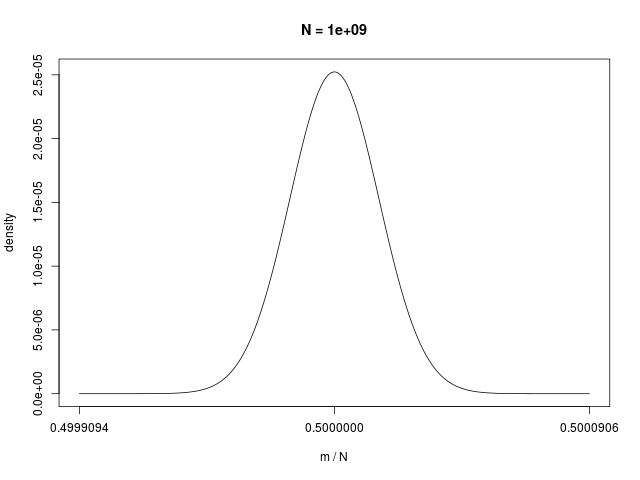ソースコード

R言語
set.seed(0)

samples <- 64*1024

logspace <- c(1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000) # logspace(0, 9, 10)

sequence <- 0
for (N in logspace) {
    val <- rbinom(samples, N, 0.5) / N
    png(paste("fig14-", formatC(sequence, width=2, flag="0"), ".png", sep=""), width=640, height=480)
    sequence <- sequence + 1
    my.min <- min(val); my.max <- max(val)
    if (abs(my.min - 0.5) < abs(my.max - 0.5))
        my.min <- 0.5 - abs(my.max - 0.5)
    else
        my.max <- 0.5 + abs(my.min - 0.5)
    hist(val, main=paste("N =", N), xlab="m / N", breaks=seq(my.min, my.max, len=20), xaxp=c(my.min, my.max, 2), col="blue", freq=FALSE)
    dev.off()
}

if (FALSE) # animation
    system("convert -delay 100 -loop 0 fig14-*.png fig14.gif")
set.seed(0)

logspace <- c(1, 10, 100, 1000, 10000, 100000, 1000000, 10000000, 100000000, 1000000000) # logspace(0, 9, 10)

get.range <- function(N) { # adhoc
    samples <- 64*1024
    val <- rbinom(samples, N, 0.5)
    my.min <- min(val); my.max <- max(val)
    if (abs(my.min - (N/2)) < abs(my.max - (N/2)))
        my.min <- (N/2) - abs(my.max - (N/2))
    else
        my.max <- (N/2) + abs(my.min - (N/2))
    return(c(my.min, my.max))
}

sequence <- 0
for (N in logspace) {
    png(paste("fig15-", formatC(sequence, width=2, flag="0"), ".png", sep=""), width=640, height=480)
    sequence <- sequence + 1
    my.range <- get.range(N)
    m <- seq(my.range[1], my.range[2], length=1024)
    plot(m/N, dbinom(round(m), N, 0.5), main=paste("N =", N), xlab="m / N", ylab="density", xaxp=c(my.range[1]/N, my.range[2]/N, 2), type="l")
    dev.off()
}

if (FALSE) # animation
    system("convert -delay 100 -loop 0 fig15-*.png fig15.gif")

多次元ガウス分布(multivariate Gaussian distribution)

\( D \) 次元ベクトル \( \mathbf x \) の多次元ガウス分布

\[ \mathcal{N}(\mathbf{x}|\boldsymbol \mu,\boldsymbol \Sigma) = \frac{1}{(2\pi)^{D/2}}\frac{1}{|\boldsymbol\Sigma|^{1/2}}\exp\left\{ -\frac{1}{2}(\mathbf x - \boldsymbol\mu)^\mathrm T\boldsymbol\Sigma^{-1}(\mathbf x - \boldsymbol\mu) \right\} \]

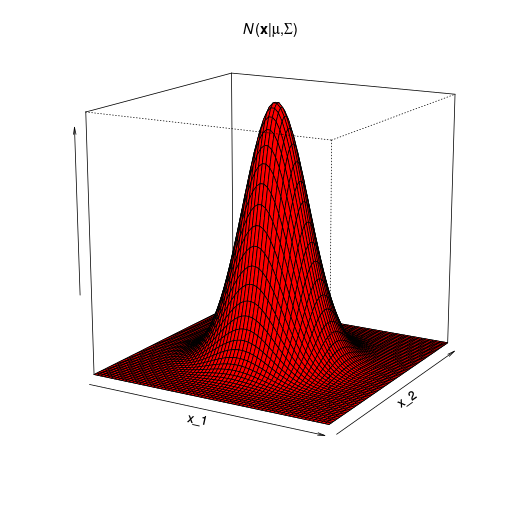\( \boldsymbol \mu \)：\( D \)次元平均ベクトル
\( \boldsymbol \Sigma \)：\( D \times D \)共分散行列
\( |\boldsymbol \Sigma| \)：\( \boldsymbol \Sigma \)の行列式

\( D \)が１次元の場合

cf. 
\[ \mathcal{N}(x|\mu,\sigma^2) = \frac{1}{(2\pi\sigma^2)^{1/2}}\exp\left\{ -\frac{1}{2\sigma^2}(x - \mu)^2 \right\} = \frac{1}{(2\pi)^{1/2}}\frac{1}{(\sigma^2)^{1/2}}\exp\left\{ -\frac{1}{2}\frac{1}{\sigma^2}(x - \mu)^2 \right\} \]
\( \mu \)：平均
\( \sigma^2 \)：分散

多次元ガウス分布のライブラリ

R言語のmvtnormパッケージのインストール（私の環境ではapt）

Linux
$ sudo apt install r-cran-mvtnorm

利用例のサンプルコード

R言語
library(mvtnorm)

y <- x <- seq(-4, 4, length=64)
z <- outer(x, y, function(x, y) { mu <- c(0, 0); Sigma <- 1*diag(2); dmvnorm(cbind(x, y), mu, Sigma) })

png("fig16.png", width=512, height=512)
persp(x, y, z, main=expression(paste(italic(N),"(", bold(x), "|", bold(mu), ",", bold(Sigma), ")")), xlab="x_1", ylab="x_2", zlab="", theta=30, r=10, col="red")
dev.off()

多次元ガウス分布の期待値と共分散

\( \mathbf x \)が多次元ガウス分布に従うとき\[ \mathbb E[\mathbf x] = \boldsymbol \mu \]\[ \mathbb E[\mathbf x \mathbf{x}^\mathrm T] = \boldsymbol \mu \boldsymbol{\mu}^\mathrm T + \boldsymbol \Sigma \]\[ \mathrm{cov}[\mathbf x] = \boldsymbol \Sigma \]となる（導出は教科書）

共分散行列

（\( \boldsymbol \Sigma \)の固有ベクトル\( \mathbf u_1, \ldots, \mathbf u_D \)）

共分散行列が、一般(general form)の場合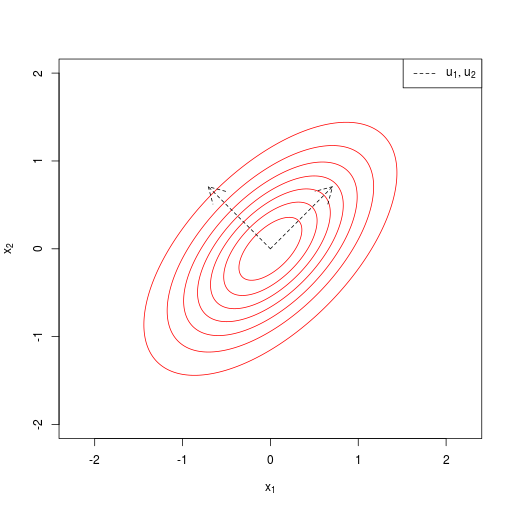
対角行列(diagonal)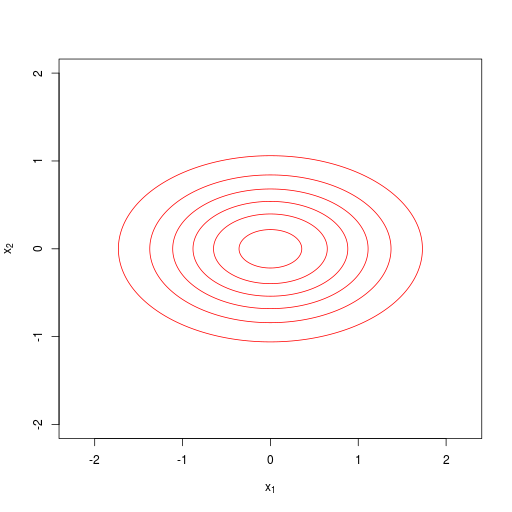
\[ \boldsymbol \Sigma = \mathrm{diag}(\sigma^2_i) = \begin{pmatrix} \sigma^2_1 & & & 0 \\ & \sigma^2_2 & & \\ & & \ddots & \\ 0 & & & \sigma^2_D \end{pmatrix} \]
単位行列に比例(proportional to the identity matrix)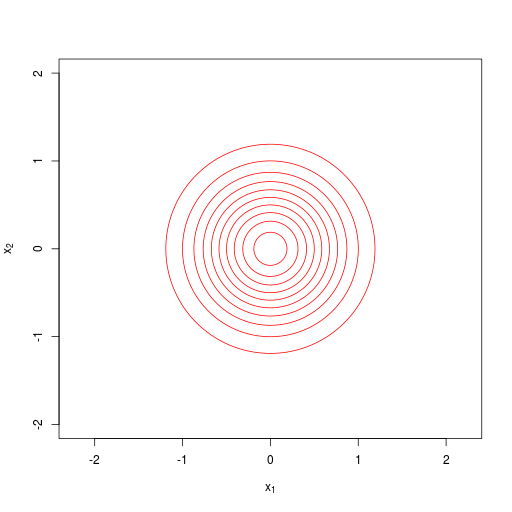
等方共分散行列(isotropic covariance matrices)
（等方的なガウス分布）
\[ \boldsymbol \Sigma = \sigma^2 \mathbf{I} = \begin{pmatrix} \sigma^2 & & & 0 \\ & \sigma^2 & & \\ & & \ddots & \\ 0 & & & \sigma^2 \end{pmatrix} \]

ソースコード

R言語
library(mvtnorm)

y <- x <- seq(-2, 2, len=1024)

mu <- c(0, 0)

Sigma <- matrix(c(0.5, 0.3, 0.3, 0.5), nrow=2)
z <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))
u <- eigen(Sigma)
png("fig17.png", width=512, height=512)
contour(x, y, z, asp=1, drawlabels=FALSE, xlab=quote(x[1]), ylab=quote(x[2]), col="red")
arrows(mu[1], mu[2], u$vectors[1,1], u$vectors[2,1], lty="dashed")
arrows(mu[1], mu[2], u$vectors[1,2], u$vectors[2,2], lty="dashed")
legend("topright", legend=expression(list(u[1],u[2])), lty="dashed")
dev.off()

Sigma <- diag(c(0.8, 0.3))
z <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))
png("fig18.png", width=512, height=512)
contour(x, y, z, asp=1, drawlabels=FALSE, xlab=quote(x[1]), ylab=quote(x[2]), col="red")
dev.off()

Sigma <- 0.3*diag(2)
z <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))
png("fig19.png", width=512, height=512)
contour(x, y, z, asp=1, drawlabels=FALSE, xlab=quote(x[1]), ylab=quote(x[2]), col="red")
dev.off()

【公式】条件付きガウス分布(conditional Gaussian distribution)、周辺ガウス分布(marginal Gaussian distribution)

（結論として、）多変数ガウス分布の重要な性質は、条件付きガウス分布も、周辺分布も、同様にガウス分布になる

同時ガウス分布 \( \mathcal{N}(\mathbf x|\boldsymbol \mu, \boldsymbol \Sigma) \)\[ \mathbf{x} = \begin{pmatrix} \mathbf x_a \\ \mathbf x_b \end{pmatrix},\ \boldsymbol \mu = \begin{pmatrix} \boldsymbol \mu_a \\ \boldsymbol \mu_b \end{pmatrix} \]\[ \boldsymbol \Sigma = \begin{pmatrix} \boldsymbol \Sigma_{aa} & \boldsymbol \Sigma_{ab} \\ \boldsymbol \Sigma_{ba} & \boldsymbol \Sigma_{bb} \end{pmatrix},\ \boldsymbol \Lambda = \begin{pmatrix} \boldsymbol \Lambda_{aa} & \boldsymbol \Lambda_{ab} \\ \boldsymbol \Lambda_{ba} & \boldsymbol \Lambda_{bb} \end{pmatrix} \equiv \boldsymbol \Sigma^{-1} \]

共分散行列の逆行列\[ \boldsymbol \Lambda \equiv \boldsymbol \Sigma^{-1} \]を精度行列(precision matrix)。ここで強調されるべきことは、\[ \begin{pmatrix} \boldsymbol \Lambda_{aa} & \boldsymbol \Lambda_{ab} \\ \boldsymbol \Lambda_{ba} & \boldsymbol \Lambda_{bb} \end{pmatrix} \equiv \begin{pmatrix} \boldsymbol \Sigma_{aa} & \boldsymbol \Sigma_{ab} \\ \boldsymbol \Sigma_{ba} & \boldsymbol \Sigma_{bb} \end{pmatrix}^{-1} \]たとえば、\( \boldsymbol \Lambda_{aa} \) は単純に \( \boldsymbol \Sigma_{aa} \) の逆行列によって与えられるわけではない

条件付き分布\[ p(\mathbf x_a|\mathbf x_b) = \mathcal N(\mathbf x_a|\boldsymbol\mu_{a|b}, \mathbf \Lambda_{aa}^{-1}) \]\[ \boldsymbol\mu_{a|b} = \boldsymbol\mu_a - \boldsymbol\Lambda_{aa}^{-1}\boldsymbol\Lambda_{ab}(\mathbf x_b - \boldsymbol\mu_b) \]

周辺分布\[ p(\mathbf x_a) = \mathcal N(\mathbf x_a|\boldsymbol\mu_a, \boldsymbol \Sigma_{aa}) \]

（導出は教科書）

【公式】ガウス変数に対してのベイズの定理

ガウス周辺分布 \( p(\mathbf x) \) とガウス条件付き分布 \( p(\mathbf y|\mathbf x) \) が与えられていると仮定。周辺分布 \( p(\mathbf y)\) と条件付き分布 \( p(\mathbf x|\mathbf y) \) を求めたい\[ p(\mathbf{x}) = \mathcal N(\mathbf x|\boldsymbol\mu, \boldsymbol\Lambda^{-1}) \]\[ p(\mathbf y|\mathbf x) = \mathcal N(\mathbf y|\mathbf{A x} + \mathbf b,\mathbf L^{-1}) \]ただし、\( \boldsymbol\mu \)、\( \mathbf A \)、\( \mathbf b \) は平均を決定するパラメータ、\( \boldsymbol\Lambda \) と \( \mathbf L \) は精度行列

（一般解）

\( \mathbf y \) の周辺分布と \( \mathbf y \) が与えられた \( \mathbf x \) の条件付き分布\[ p(\mathbf y) = \mathcal N(\mathbf y|\mathbf A\boldsymbol\mu + \mathbf b, \mathbf L^{-1} + \mathbf A\boldsymbol\Lambda^{-1}\mathbf A^\mathrm T) \]\[ p(\mathbf x|\mathbf y) = \mathcal N(\mathbf x|\boldsymbol\Sigma\{ \mathbf A^\mathrm T\mathbf L(\mathbf y - \mathbf b) + \boldsymbol{\Lambda \mu} \}, \boldsymbol\Sigma) \]

ただし\[ \boldsymbol\Sigma = (\mathbf\Lambda + \mathbf A^\mathrm T\mathbf L\mathbf A)^{-1} \]

（導出は教科書）

ガウス分布の最尤推定(maximum likelihood)

（パラメータ推定）

観測値のデータ集合\[ \mathcal D = \{ x_1,\ldots,x_N \} \]これらが、ガウス分布からそれぞれ独立に得られたとする（独立同分布(i.i.d.)を仮定）

尤度関数\[ p(\mathcal D|\mu,\sigma^2) = \prod_{n=1}^N\mathcal N(x_n|\mu,\sigma^2) = \prod_{n=1}^N\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{1}{2\sigma^2}(x_n - \mu)^2 \right\} \]

（尤度、尤度関数。同時確率分布の式\[ \mathbf x = (x_1,\ldots,x_N)^\mathrm T,\ p(\mathbf x|\mu,\sigma^2) = \prod_{n=1}^N\mathcal N(x_n|\mu,\sigma^2) \]を、観測データ \( \mathbf x \) を固定して、（データの背後にある）確率分布のパラメタ \(\mu,\sigma^2\) の方を変数としてみる。（同じ式を、式の見方を変える。）尤度関数は確率ではないので、変数が取り得る全ての範囲を積分しても \( 1 \) にはならない。尤度関数の値（尤度）は、そのパラメタがもとの確率分布を表している尤もらしさ）

（尤度を最大化する（最も尤もらしい） \( \mu,\sigma^2 \) を求める）

対数尤度関数\[ \ln p(\mathcal D|\mu,\sigma^2) = -\frac{1}{2\sigma^2}\sum_{n=1}^N(x_n - \mu)^2 - \frac{N}{2}\ln \sigma^2 - \frac{N}{2}\ln 2\pi \]

対数尤度を最大化するパラメータを求める（対数尤度関数をパラメタで偏微分して \( 0 \) となるところ）\[ \frac{\partial}{\partial\mu}\ln p(\mathcal D|\mu,\sigma^2) = 0,\ \frac{\partial}{\partial\sigma^2}\ln p(\mathcal D|\mu,\sigma^2) = 0 \]（計算省略）

最尤推定解

\[ \mu_\mathrm{ML} = \frac{1}{N}\sum_{n=1}^N x_n ~ \] ←サンプル平均
\[ \sigma^2_\mathrm{ML} = \frac{1}{N}\sum_{n=1}^N(x_n - \mu_\mathrm{ML})^2 ~ \] ←サンプル分散
（\( \mu_\mathrm{ML} \) は \( \mu \) の（もとのガウス分布の平均の）不偏推定量になっているが、\( \sigma^2_\mathrm{ML}\) は \( \sigma^2 \) の（もとのガウス分布の分散の）不偏推定量になっていない）

\( D \) 次元の多次元ガウス分布の最尤推定解

尤度関数\[ ~~~ p(\mathbf X|\boldsymbol\mu, \boldsymbol\Sigma) = \prod_{n=1}^N\mathcal N(\mathbf x_n|\boldsymbol\mu, \mathbf\Sigma) = \prod_{n=1}^N\left[ \frac{1}{(2\pi)^\frac{D}{2}|\mathbf\Sigma|^{\frac{1}{2}}}\exp\left\{ -\frac{1}{2}(\mathbf x_n - \boldsymbol\mu)^\mathrm T\boldsymbol\Sigma^{-1}(\mathbf x_n - \boldsymbol\mu) \right\} \right] ~~~ \]

対数尤度関数\[ \ln p(\mathbf X|\boldsymbol\mu, \boldsymbol\Sigma) = -\frac{ND}{2}\ln(2\pi) - \frac{N}{2}\ln|\boldsymbol \Sigma| - \frac{1}{2}\sum_{n=1}^N(\mathbf x_n - \boldsymbol\mu)^\mathrm T\boldsymbol\Sigma^{-1}(\mathbf x_n - \mu) \]

対数尤度を最大化\[ \frac{\partial}{\partial\boldsymbol\mu}\ln p(\mathbf X|\boldsymbol\mu, \boldsymbol\Sigma) = 0,\ \frac{\partial}{\partial\boldsymbol\Sigma}\ln p(\mathbf X|\boldsymbol\mu, \boldsymbol\Sigma) = 0 \]

最尤推定解\[ \begin{align} \boldsymbol\mu_\mathrm{ML} &= \frac{1}{N}\sum_{n=1}^N\mathbf x_n \\ \boldsymbol\Sigma_\mathrm{ML} &= \frac{1}{N}\sum_{n=1}^N(\mathbf x_n - \boldsymbol\mu_\mathrm{ML})(\mathbf x_n - \boldsymbol\mu_\mathrm{ML})^\mathrm T \end{align} \]（サンプル平均とサンプル共分散）

ガウス分布のベイズ推定(Bayesian inference)

ベイズ確率

事後確率 ∝ 尤度 × 事前確率
( posterior ∝ likelihood × prior )

ベイズの定理\[ p(\boldsymbol\theta|\mathcal D) = \frac{p(\mathcal D|\boldsymbol\theta)p(\boldsymbol\theta)}{p(\mathcal D)} \]（ベイズの定理の分母 \( p(\mathcal D) \) は（規格化）定数）

\[ p(\boldsymbol\theta|\mathcal D) \propto p(\mathcal D|\boldsymbol\theta)p(\boldsymbol\theta) \]（確率変数 \( \boldsymbol\theta \) は推定されるパラメタ、\( \mathcal D \) は観測データ。\( p(\boldsymbol\theta|\mathcal D) \) は、データ \( \mathcal D \) が観測されたという条件のもとでパラメタが \( \boldsymbol\theta \) となる確率。\( p(\mathcal D|\boldsymbol\theta) \) は尤度関数で、パラメタが \( \boldsymbol\theta \) であったとしたときにデータ \( \mathcal D \) が観測される尤もらしさ（同時確率を、\( \boldsymbol\theta \) を変数とみなす）。\( p(\boldsymbol\theta) \) は、どのようなデータ \( \mathcal D \) が観測されるかに関わらず、パラメタが \( \boldsymbol\theta \) となる確率）

（逐次推定(sequential estimation)と共役事前分布(conjugate prior)について）

（MAP(maximum a posteriori)推定（最大事後確率推定）について → 事後確率分布のモード（最頻値）を（予測値として）採用）

ガウス分布\[ \mathcal N(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{1}{2\sigma^2}(x - \mu)^2 \right\} \]は、平均 \( \mu \) と分散 \( \sigma^2 \) の２つのパラメタを持つため

  1. 平均のみ推定（分散は既知とする）
  2. 分散のみ推定（平均は既知とする）
  3. 平均と分散の両方を推定
の３パタンがある

平均 \( \mu \) の推定（分散 \( \sigma^2 \) は既知）

（たとえば、事前に実験するなどしてセンサーノイズの分散を決定してある、というような場合）

尤度関数\[ \begin{align} p(\mathbf x|\mu) &= \prod_{n=1}^N \mathcal N(x_n|\mu,\sigma^2) \\ &= \prod_{n=1}^N \frac{1}{(2\pi\sigma^2)^{1/2}}\exp\left\{ -\frac{1}{2\sigma^2}(x_n - \mu)^2 \right\} \\ &= \frac{1}{(2\sigma^2)^{N/2}}\exp\left\{ -\frac{1}{2\sigma^2}\sum_{n=1}^N(x_n - \mu)^2 \right\} \end{align} \]

共役事前分布（は、ガウス分布）\[ p(\mu) = \mathcal N(\mu|\mu_0,\sigma^2_0) = \frac{1}{(2\pi\sigma^2_0)^{1/2}}\exp\left\{ -\frac{1}{2\sigma^2_0}(\mu - \mu_0)^2 \right\} \]（\( \mu_0, \sigma^2_0 \) は超パラメタ(hyperparameter)）

事後分布（まず \( \mu \) について式を整理する）\[ \begin{align} ~~~ p(\mu|\mathbf x) &\propto p(\mathbf x|\mu)p(\mu) \\ &\propto \exp\left\{ -\frac{1}{2\sigma^2}\sum_n(\mu - x_n)^2 - \frac{1}{2\sigma^2_0}(\mu - \mu_0)^2 \right\} \\ &= \exp \left\{ -\left( \frac{N}{2\sigma^2} + \frac{1}{2\sigma^2_0} \right)\mu^2 + 2\left( \frac{\sum_n x_n}{2\sigma^2} + \frac{\mu_0}{2\sigma^2_0} \right)\mu + \mathrm{const.} \right\} ~~~ \end{align} \]

… 平方完成
\[ \therefore p(\mu|\mathbf x) = \mathcal N(\mu|\mu_N,\sigma^2_N) \] ただし、 \[ \mu_N = \frac{\sigma^2}{N\sigma^2_0 + \sigma^2}\mu_0 + \frac{N\sigma^2_0}{N\sigma^2 + \sigma^2}\mu_\mathrm{ML},\ \frac{1}{\sigma^2_N} = \frac{1}{\sigma^2_0} + \frac{N}{\sigma^2} \]（\( \mu_\mathrm{ML} \) は \( \mu \) の最尤推定解）

分散 \( \sigma^2 \) の推定（平均 \( \mu \) は既知）

（たとえば、リファレンス信号を入力してセンサーノイズの分散を測定する、というような場合）

尤度関数\[ \begin{align} p(\mathbf x|\lambda) &= \prod_{n=1}^N\mathcal N(x_n|\mu,\lambda^{-1}) \\ &= \prod_n\sqrt\frac{\lambda}{2\pi}\exp\left\{ -\frac{\lambda}{2}(x_n - \mu)^2 \right\} \\ &\propto \lambda^\frac{N}{2}\exp\left\{ -\frac{\sum_n(x_n - \mu)^2}{2}\lambda \right\} \end{align} \]（精度 \( \lambda \equiv 1/\sigma^2 \)）

共役事前分布（ガンマ分布）\[ \begin{align} p(\lambda) &= \mathrm{Gam}(\lambda|a_0,b_0) = \frac{1}{\Gamma(a_0) }b_0^{a_0}\lambda^{a_0 - 1}\exp(-b_0\lambda) \\ &\propto \lambda^{a_0 - 1}\exp(-b_0\lambda) \end{align} \]（\( a_0, b_0 \) はハイパーパラメタ）

事後分布\[ p(\lambda|\mathbf x) = p(\mathbf x|\lambda)p(\lambda) = \mathrm{Gam}(\lambda|a_N,b_N) \]ただし、\[ ~~~ a_N = a_0 + \frac{N}{2},\ b_N = b_0 + \sum_n\frac{(x_n - \mu)^2}{2} = b_0 + \frac{N}{2}\sigma^2_\mathrm{ML} ~~~ \]（\( \sigma^2_\mathrm{ML} \) は \( \sigma^2 \) の最尤推定解）

（「平均と分散の推定」については、PRMLに結論の式の記載なし）

共役事前分布

（早見表）
もとの確率分布推定したいパラメタ共役事前分布
ベルヌーイ分布\[ \mathrm{Bern}(x|\mu) \]\[ \mu \]ベータ分布\[ \mathrm{Beta}(\mu|a,b) \]
二項分布\[ \mathrm{Bin}(m|N,\mu) \]\[ \mu \]ベータ分布\[ \mathrm{Beta}(\mu|a,b) \]
ガウス分布\[ \mathcal N(x|\mu,\sigma^2) \]\[ \mu \]ガウス分布\[ \mathcal{N}(\mu|\mu_0,\sigma^2_0) \]
ガウス分布\[ \mathcal N(x|\mu,\lambda^{-1}) \]\[ \lambda \]ガンマ分布\[ \mathrm{Gam}(\lambda|a,b) \]
ガウス分布\[ \mathcal N(x|\mu,\lambda^{-1}) \]\[ \mu, \lambda \]ガウス–ガンマ分布\[\mathcal N(\mu|\mu_0,(\beta\lambda)^{-1})\mathrm{Gam}(\lambda|a,b) \]
精度 \( \lambda \equiv 1/(\sigma^2) \)

多次元ガウス分布のベイズ推定

（詳細は教科書）

（分散が既知で）平均を推定する具体例

データ \( \mathcal D = \{ 1.5, 1.3, 0.5, 0.6, 1.9 \} \) が、ガウス分布 \( p(x|\mu, 0.7^2) \) からそれぞれ独立にに得られたものとする（i.i.d. を仮定）

ベイズ推定の式（こちらの式の再掲載）\[ \begin{align} \mu_N &= \frac{\sigma^2}{N\sigma^2_0 + \sigma^2}\mu_0+\frac{N\sigma^2_0}{N\sigma_0^2 + \sigma^2}\mu_\mathrm{ML} \\ \frac{1}{\sigma^2_N} &= \frac{1}{\sigma^2_0} + \frac{N}{\sigma^2} \end{align} \]

データが一つずつ観測されたものとして、逐次推定(sequential estimation)を行う

\( N=1,\ \mu_\mathrm{ML} = \mathcal D_i \) とした式\[ \begin{align} \mu_{posterior} &= \frac{\sigma^2}{\sigma^2_{prior} + \sigma^2}\mu_{prior}+\frac{\sigma^2_{prior}}{\sigma_{prior}^2 + \sigma^2}D_i \\ \frac{1}{\sigma^2_{posterior}} &= \frac{1}{\sigma^2_{prior}} + \frac{1}{\sigma^2} \end{align} \]（添え字 \( prior \) は事前確率分布のパラメタであること、\( posterior \) は事後確率分布のパラメタであることを示す）

分散は既知で \( \sigma^2 = 0.7^2 \)

事前分布のパラメタ（の初期値）は \( \mu_0 = 2,\ \sigma_0 = 0.5 \) とする（事前の信念）

ソースコード

R言語
## bel
mu_prior <- 2; sigma_prior <- 0.5

## i.i.d.
sigma <- 0.7

## observation data
D <- c(1.5, 1.3, 0.5, 0.6, 1.9)

## sequential estimation
x <- seq(0, 3, len=1024)
frame <- 0
for (i in 1:length(D)) {
    png(paste("fig20-", formatC(frame, width=2, flag="0"), ".png", sep=""), width=640, height=480); frame <- frame + 1
    plot(x, dnorm(x, mu_prior, sigma_prior), type="l", col="red", xlab=expression(italic(D)), ylab="", ylim=c(0, 1.5), main=paste("i =", i))
    legend("topleft", legend="prior (belief)", col="red", lty=1)
    dev.off()

    ## observation
    png(paste("fig20-", formatC(frame, width=2, flag="0"), ".png", sep=""), width=640, height=480); frame <- frame + 1
    plot(x, dnorm(x, mu_prior, sigma_prior), type="l", col="red", xlab=expression(italic(D)), ylab="", ylim=c(0, 1.5), main=paste("i =", i))
    points(D[i], 0, pch=16, col="blue")
    legend("topleft", legend=c("prior", "observation"),  col=c("red", "blue"), lty=c(1, 0), pch=c(NA, 16))
    dev.off()

    ## likelihood
    png(paste("fig20-", formatC(frame, width=2, flag="0"), ".png", sep=""), width=640, height=480); frame <- frame + 1
    plot(x, dnorm(x, mu_prior, sigma_prior), type="l", col="red", xlab=expression(italic(D)), ylab="", ylim=c(0, 1.5), main=paste("i =", i))
    points(D[i], 0, col="skyblue")
    lines(c(D[i], D[i]), c(0, dnorm(D[i], D[i], sigma)), lty="dashed", col="skyblue")
    lines(x, dnorm(x, D[i], sigma), type="l", col="blue")
    legend("topleft", legend=c("prior", "likelihood"), col=c("red", "blue"), lty=1)
    dev.off()

    ## Bayesian inference
    mu_posterior <- (sigma^2/(sigma_prior^2 + sigma^2))*mu_prior + (sigma_prior^2/(sigma_prior^2 + sigma^2))*D[i]
    sigma_posterior <- sqrt((1/sigma_prior^2 + 1/sigma^2)^-1)

    png(paste("fig20-", formatC(frame, width=2, flag="0"), ".png", sep=""), width=640, height=480); frame <- frame + 1
    plot(x, dnorm(x, mu_posterior, sigma_posterior), type="l", col="red", xlab=expression(italic(D)), ylab="", ylim=c(0, 1.5), main=paste("i =", i))
    lines(x, dnorm(x, D[i], sigma), type="l", col="blue")
    legend("topleft", legend=c("posterior", "likelihood"), col=c("red", "blue"), lty=1)
    dev.off()

    ## MAP
    mu_MAP <- mu_posterior # x[which.max(dnorm(x, mu_posterior, sigma_posterior))]

    png(paste("fig20-", formatC(frame, width=2, flag="0"), ".png", sep=""), width=640, height=480); frame <- frame + 1
    plot(x, dnorm(x, mu_posterior, sigma_posterior), type="l", col="red", xlab=expression(italic(D)), ylab="", ylim=c(0, 1.5), main=paste("i =", i))
    lines(c(mu_MAP, mu_MAP), c(0, dnorm(mu_MAP, mu_posterior, sigma_posterior)), lty="dashed", col="red")
    legend("topleft", legend=c("posterior", "MAP"), col=c("red", "red"), lty=c(1, 2))
    dev.off()

    ## update bel
    mu_prior <- mu_posterior
    sigma_prior <- sigma_posterior
}

if (FALSE) # animation
    system("convert -delay 100 -loop 0 fig20-*.png fig20.gif")

## show parameter
## (mu_posterior); (sigma_posterior)

\( N = 5 \) のデータをバッチ処理した結果と検算

プログラムで確認

R言語
## prior
mu_0 <- 2; sigma_0 <- 0.5

## i.i.d.
sigma <- 0.7

## observation data
D <- c(1.5, 1.3, 0.5, 0.6, 1.9)
N <- length(D)

## batch processing
mu_ML <- sum(D)/N
mu_N <- (sigma^2/(N*sigma_0^2 + sigma^2))*mu_0 + ((N*sigma_0^2)/(N*sigma_0^2 + sigma^2))*mu_ML

sigma_N <- sqrt((1/sigma_0^2 + N/sigma^2)^-1)

## show parameter
(mu_N); (sigma_N)
 > ## show parameter
 > (mu_N); (sigma_N)
 [1] 1.396552
 [1] 0.2653343

推定されたパラメタはどちらも \( \mu_N = 1.396552,\ \sigma_N = 0.2653343 \) で、逐次推定した推定結果とバッチ処理した推定結果は等しい

混合ガウス分布(mixture of Gaussians)

ガウス分布は単峰形(unimodal)である。ガウス分布のような基本的な分布をいくつか線形結合して、多峰形(multimodal)の分布を表現
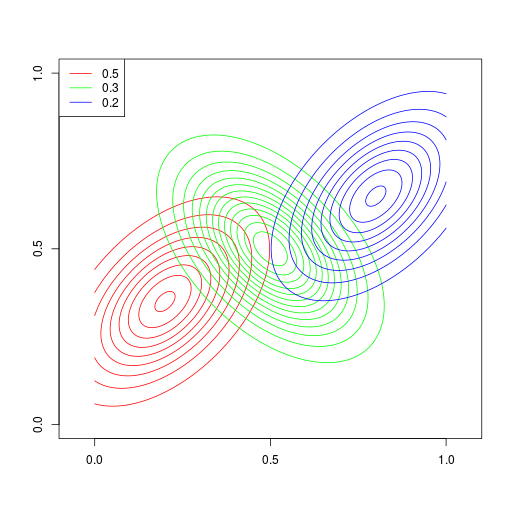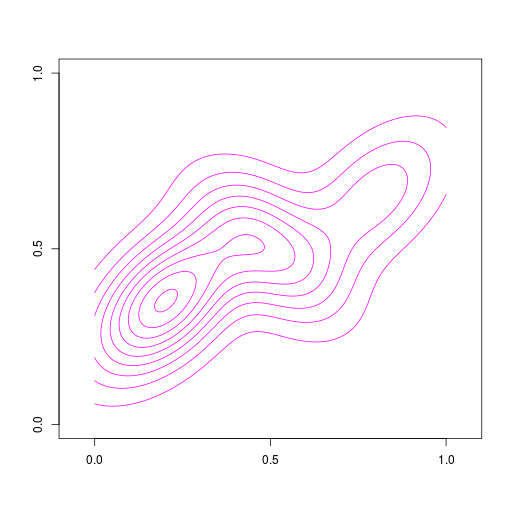混合係数(mixing coefficient)は、それぞれ 赤 0.5、緑 0.3、青 0.2

ソースコード

R言語
library(mvtnorm)

y <- x <- seq(0, 1, len=1024)

mu <- c(0.2, 0.35)
Sigma <- matrix(c(0.02, 0.01, 0.01, 0.02), nrow=2)
z.R <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))

mu <- c(0.5, 0.5)
Sigma <- matrix(c(0.02, -0.01, -0.01, 0.02), nrow=2)
z.G <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))

mu <- c(0.8, 0.65)
Sigma <- matrix(c(0.02, 0.01, 0.01, 0.02), nrow=2)
z.B <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))

## mixing coefficient
z.R <- z.R * 0.5
z.G <- z.G * 0.3
z.B <- z.B * 0.2

png("fig21.png", width=512, height=512)
contour(x, y, z.R, asp=1, drawlabels=FALSE, col="red", xaxp=c(0, 1, 2), yaxp=c(0, 1, 2))
contour(x, y, z.G, asp=1, drawlabels=FALSE, col="green", add=TRUE, axes=FALSE)
contour(x, y, z.B, asp=1, drawlabels=FALSE, col="blue", add=TRUE, axes=FALSE)
legend("topleft", legend=c("0.5", "0.3", "0.2"), col=c("red", "green", "blue"), lty=c("solid"))
dev.off()

png("fig22.png", width=512, height=512)
contour(x, y, (z.R + z.G + z.B), asp=1, drawlabels=FALSE, col=rgb(1, 0, 1), xaxp=c(0, 1, 2), yaxp=c(0, 1, 2))
dev.off()
library(mvtnorm)

y <- x <- seq(0, 1, len=64)

mu <- c(0.2, 0.35)
Sigma <- matrix(c(0.02, 0.01, 0.01, 0.02), nrow=2)
z.R <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))

mu <- c(0.5, 0.5)
Sigma <- matrix(c(0.02, -0.01, -0.01, 0.02), nrow=2)
z.G <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))

mu <- c(0.8, 0.65)
Sigma <- matrix(c(0.02, 0.01, 0.01, 0.02), nrow=2)
z.B <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), mu, Sigma))

## mixing coefficient
z.R <- z.R * 0.5
z.G <- z.G * 0.3
z.B <- z.B * 0.2

for (angle in seq(0, (360 - 30), by=30)) {
    png(paste(paste("fig23", formatC(angle, width=3, flag="0"), sep="-"), "png", sep="."), width=512, height=512)
    persp(x, y, (z.R + z.G + z.B), theta=angle, phi=30, r=10, col=rgb(1, 0.5, 0), shade=0.5, box=FALSE)
    dev.off()
}

if (FALSE) # animation
    system("convert -delay 100 -loop 0 fig23-*.png fig23.gif")

ノンパラメトリック(nonparametric)

ヒストグラム密度推定(histogram density estimation)

ビンの幅 \( \Delta \) を適切に決定する必要がある

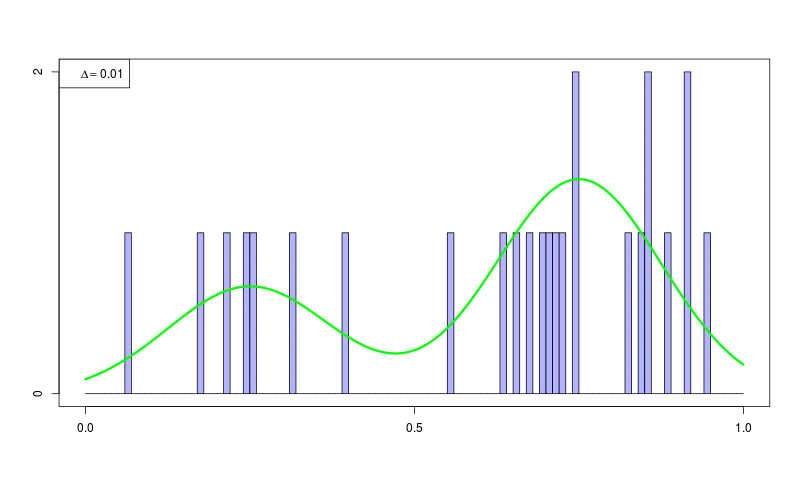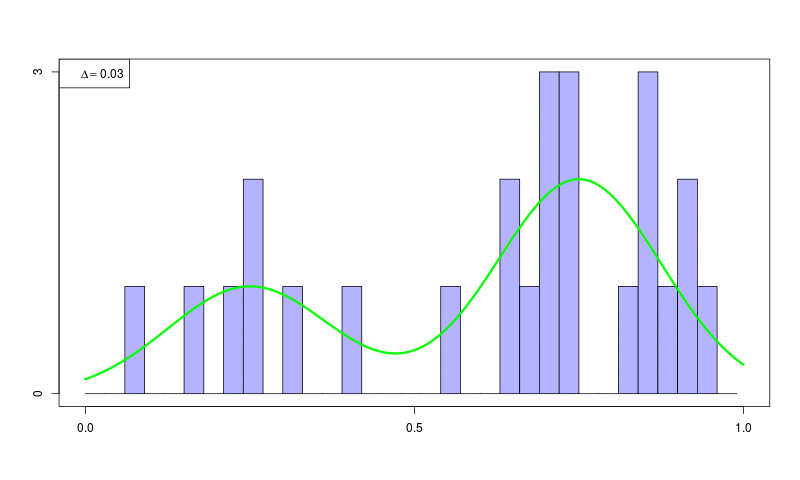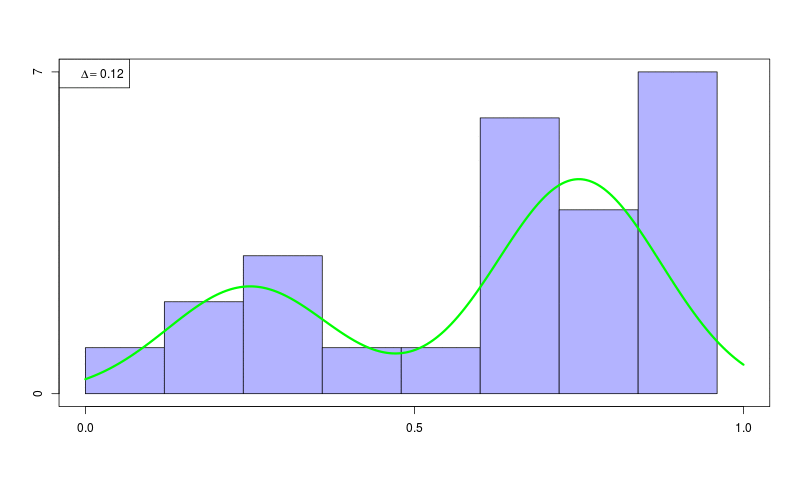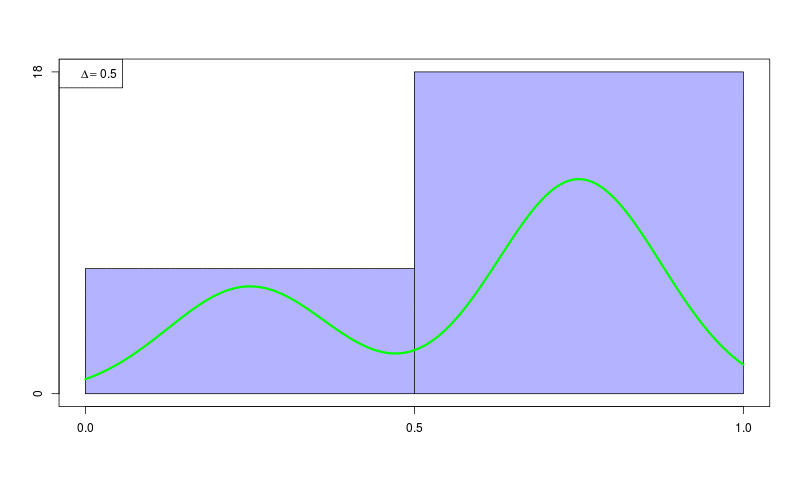
ソースコード

R言語
set.seed(0)

sample <- rep(0, 25)
for (i in 1:length(sample)) {
    if (runif(1) < (1/3))
        repeat { # adhoc
            sample[i] <- rnorm(1, 0.25, 0.125)
            if (0 <= sample[i] && sample[i] <= 1) break;
        }
    else
        repeat { # adhoc
            sample[i] <- rnorm(1, 0.75, 0.125)
            if (0 <= sample[i] && sample[i] <= 1) break;
        }
}

i <- 0; x <- seq(0, 1, len=1024)
for (delta in round(1/c(128, 64, 32, 16, 8, 4, 2), 2)) {
    png(paste("fig24-", i, ".png", sep=""), width=800, height=480); i <- i + 1
    my.hist <- hist(sample, main="", xlab="", ylab="", xlim=c(0, 1), xaxp=c(0, 1, 2), yaxt="n", col="#B3B3FF", breaks=seq(0, 1, by=delta))
    axis(side=2, at=c(0, max(my.hist$counts)))
    y <- dnorm(x, 0.25, 0.125)*(1/3) + dnorm(x, 0.75, 0.125)*(2/3)
    scale <- (max(my.hist$counts)/max(y))*(2/3); y <- y*scale # adhoc
    lines(x, y, lwd=3, col="green")
    legend("topleft", legend=bquote(Delta == .(delta)))
    box()
    dev.off()
}

if (FALSE) # animation
    system("convert -delay 100 -loop 0 fig24-*.png fig24.gif")

カーネル密度推定

R言語のdensity()関数

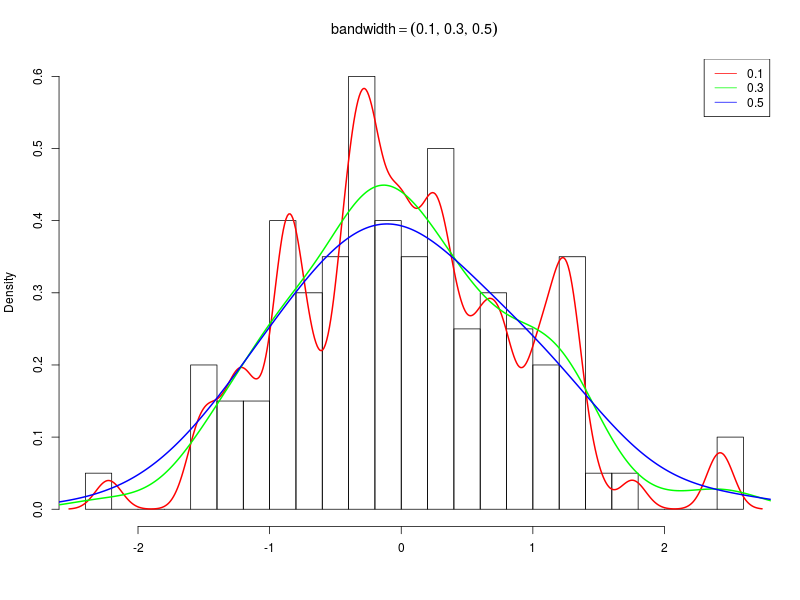
ソースコード

R言語
set.seed(0)
x <- rnorm(100, 0, 1)

png("fig25.png", width=800, height=600)
hist(x, main=expression(bandwidth == (list(0.1, 0.3, 0.5))), xlab="", breaks=20, freq=FALSE)
lines(density(x, bw=0.1), lwd=2, col="red")
lines(density(x, bw=0.3), lwd=2, col="green")
lines(density(x, bw=0.5), lwd=2, col="blue")
legend("topright", legend=c("0.1", "0.3", "0.5"), col=c("red", "green", "blue"), lty=1)
dev.off()

２次元のカーネル密度推定。R言語のMASSパッケージを利用

kde2d()関数の使用例

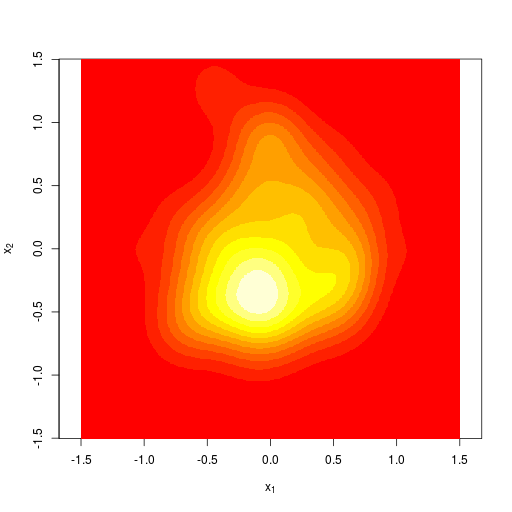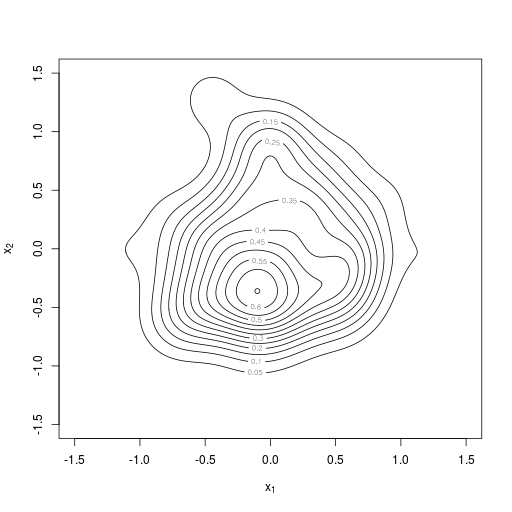MASSパッケージのインストール（私の環境ではapt）

Linux
$ sudo apt install r-cran-mass

ソースコード

R言語
library(MASS)

set.seed(0)
x <- rnorm(100, 0, 0.5); y <- rnorm(100, 0, 0.5)

png("fig26.png", width=512, height=512)
plot(x, y, xlab=expression(x[1]), ylab=expression(x[2]), xlim=c(-1.5, 1.5), ylim=c(-1.5, 1.5), asp=1)
dev.off()

dense <- kde2d(x, y, c(bandwidth.nrd(x), bandwidth.nrd(y)), n=512, lims=c(-1.5, 1.5, -1.5, 1.5))

png("fig27.png", width=512, height=512)
image(dense, asp=1, xlab=expression(x[1]), ylab=expression(x[2]))
dev.off()

png("fig28.png", width=512, height=512)
contour(dense, xlab=expression(x[1]), ylab=expression(x[2]))
dev.off()

線形回帰(linear regression)モデル

目標変数(target variable) = 平均（多項式）+ ガウスノイズ\[ t = y(\mathbf x,\mathbf w) + \epsilon \]

\( \epsilon \) は、平均が 0 で精度 \( \beta \) のガウス分布の確率変数

確率の式として書く（\( \beta \) は精度で、分散の逆数(inverse variance)）\[ p(t|\mathbf x, \mathbf w, \beta) = \mathcal N(t|y(\mathbf x, \mathbf w), \beta^{-1}) \]入力 \( \mathbf x \) を省略して\[ p(t|\mathbf w, \beta) = \mathcal N(t|y(\mathbf x, \mathbf w), \beta^{-1}) \]

\( x \) が与えられた \( t \) の条件付きガウス分布

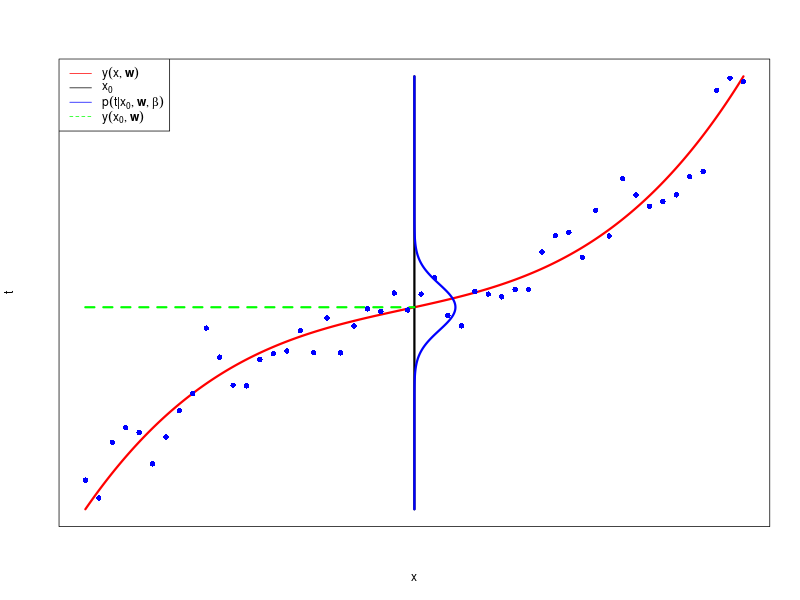
ソースコード

R言語
png("fig29.png", width=800, height=600)

x <- seq(-10, 10, len=1024)
y <- function(x) x^3 + x^2 + 50*x
t <- y(x)
plot(x, t, xlab=expression(x), ylab=expression(t), xaxt="n", yaxt="n", type="l", col="red", lwd=3)

lines(c(0, 0), c(min(t), max(t)), lwd=3)
sigma <- max(t)/10 # adhoc
t <- seq(min(t), max(t), len=1024)
x <- dnorm(t, 0, sigma)
x <- x * 500 # adhoc
lines(x, t, col="blue", lwd=3)

lines(c(-10, 0), c(0, 0), col="green", lwd=3, lty="dashed")

x <- seq(-10, 10, len=50)
set.seed(0)
t <- y(x) + rnorm(length(x), 0, sigma)
points(x, t, col="blue", pch=16)
legend("topleft",
       legend=c(expression(y(list(x, bold(w)))), expression(x[0]), expression(p(paste(t, "|", list(x[0], bold(w), beta)))), expression(y(list(x[0], bold(w))))),
       lty=c(1, 1, 1, 2), col=c("red", "black", "blue", "green"))

dev.off()

線形基底関数(linear basis function)モデル

入力変数の非線形な関数の線形結合を考える\[ y(\mathbf x, \mathbf w) = w_0 + \sum_{j=1}^{M-1}w_j\phi_j(\mathbf x) \]\( \phi_j(\mathbf x) \) は基底関数(basis function)

\( w_0 \) はバイアスパラメータ(bias parameter)。ダミー基底関数 \( \phi_0(\mathbf x) = 1 \)（恒等式）を導入\[ y(\mathbf x, \mathbf w) = \sum_{j=0}^{M-1}w_j\phi_j(\mathbf x) = \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x) \]ただし、\( \mathbf w = (w_0, \ldots, w_{M-1})^\mathrm T,\ \boldsymbol\phi(\mathbf x) = \left( \phi_0(\mathbf x), \ldots, \phi_{M-1}(\mathbf x) \right)^\mathrm T \)

基底関数

多項式基底関数ガウス基底関数

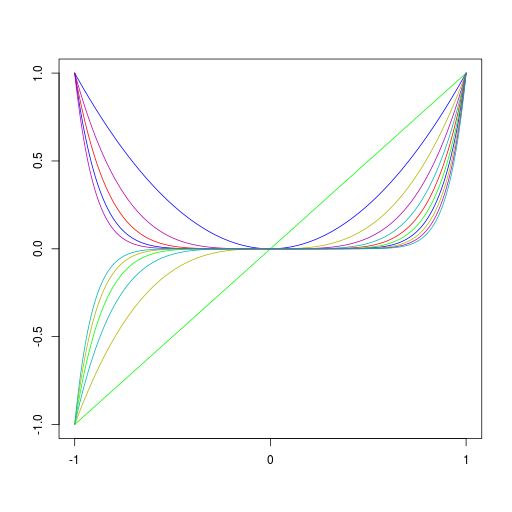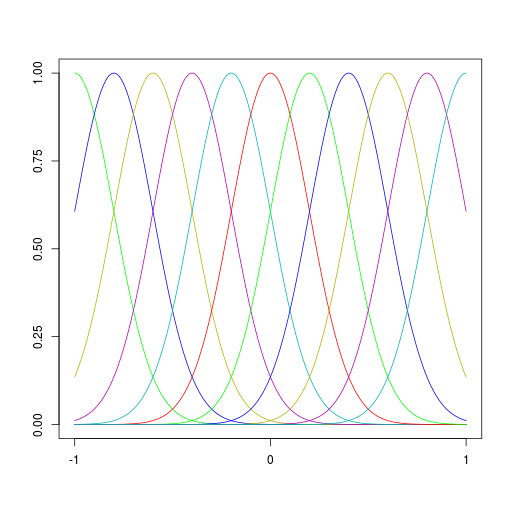\[ \phi_j(x) = x^j \]

\[ \phi_j(x) = \exp\left\{ -\frac{(x - \mu_j)^2}{2s^2} \right\} \]

（ほかにも、シグモイド基底関数やフーリエ基底など）

ソースコード

R言語
palet <- c("#00ff00", "#0000ff", "#b4b400", "#b400b4", "#00b4b4", "#ff0000",
           "#00ff00", "#0000ff", "#b4b400", "#b400b4", "#00b4b4")

x <- seq(-1, 1, length=1024)

png("fig30.png", width=512, height=512)
for (j in 1:11) {
    y <- x^j # basis function
    if (j == 1)
        plot(x, y, type="l", xlab="", ylab="", xaxp=c(-1, 1, 2), col=palet[j])
    else
        lines(x, y, col=palet[j])
}
dev.off()

png("fig31.png", width=512, height=512)
mu <- seq(-1, 1, len=11)
s <- 0.2
for (j in 1:11) {
    y <- exp(-(((x - mu[j])^2)/(2*s^2))) # basis function
    if (j == 1)
        plot(x, y, type="l", xlab="", ylab="", xaxp=c(-1, 1, 2), yaxp=c(0, 1, 4), col=palet[j])
    else
        lines(x, y, col=palet[j])
}
dev.off()

最尤推定と最小二乗法

確率の式を線形基底関数を使って書く\[ p(t|\mathbf w, \beta) = \mathcal N(t|y(\mathbf x, \mathbf w), \beta^{-1}) = \mathcal N(t|\mathbf w^\mathrm T\boldsymbol \phi(\mathbf x), \beta^{-1}) \]

入力ベクトル \( \mathbf X = (\mathbf x_1, \ldots, \mathbf x_N)^\mathrm T \)、対応する目標ベクトル(target vector) \( \mathbf t = (t_1, \ldots, t_N)^\mathrm T \) からなる訓練データ集合（\( N \) 回の観測）を考える

尤度関数\[ p(\mathbf t|\mathbf X, \mathbf w, \beta) = \prod_{n=1}^{N}\mathcal N(t_n|\mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n), \beta^{-1}) \]（i.i.d.を仮定しているので、積の形で書ける）

\( \mathbf X \) を省略して\[ p(\mathbf t|\mathbf w, \beta) = \prod_{n=1}^{N}\mathcal N(t_n|\mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n), \beta^{-1}) \]

対数尤度関数\[ \begin{align} \ln p(\mathbf t|\mathbf w,\beta) &= \sum_{n=1}^N\ln\mathcal N(t_n|\mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n),\beta^{-1}) \\ &= \frac{N}{2}\ln\beta - \frac{N}{2}\ln(2\pi) - \frac{\beta}{2}\sum_{n=1}^N\left\{ t_n - \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right\}^2 \end{align} \]（対数をとると積が和になる）

\( \mathbf w \) について対数尤度を最大化する

\( \mathbf w\) について偏微分して \( 0 \) になるところ\[ \nabla\ln p(\mathbf t|\mathbf w, \beta) = \beta\sum_{n=1}^N\left\{t_n-\mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n)\right\}\boldsymbol\phi(\mathbf x_n) = 0 \]（\( \mathbf w \) の無い項は消える。２次式の微分 ）

解き方\[ \begin{align} \beta\sum_{n=1}^N\left\{ t_n - \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right\}\boldsymbol\phi(\mathbf x_n) &= 0 \\ \sum_{n=1}^N\left\{ t_n - \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right\}\boldsymbol\phi(\mathbf x_n) &= 0 \\ \sum_{n=1}^Nt_n\boldsymbol\phi(\mathbf x_n) &= \sum_{n=1}^N\left\{ \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right\}\boldsymbol\phi(\mathbf x_n) \end{align} \]（\( \beta \) は消すことができる）

\( \sum \) 記号を行列（とベクトル）で書く\[ \begin{align} \sum_{n=1}^Nt_n\boldsymbol\phi(\mathbf x_n) &= \sum_{n=1}^N\left( \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right)\boldsymbol\phi(\mathbf x_n) \\ ~~~ \begin{pmatrix} \phi_0(\mathbf x_1) & \cdots & \phi_0(\mathbf x_N) \\ \vdots & \ddots & \vdots \\ \phi_{M-1}(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_N) \end{pmatrix}\begin{pmatrix} t_1 \\ \vdots \\ t_n \end{pmatrix} &= \begin{pmatrix} \phi_0(\mathbf x_1) & \cdots & \phi_0(\mathbf x_N) \\ \vdots & \ddots & \vdots \\ \phi_{M-1}(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_N) \end{pmatrix}\begin{pmatrix} \mathbf w^\mathrm T\boldsymbol{\phi}(\mathbf x_1) \\ \vdots \\ \mathbf w^\mathrm T\boldsymbol{\phi}(\mathbf x_N) \end{pmatrix} ~~~ \\ &= \begin{pmatrix} \phi_0(\mathbf x_1) & \cdots & \phi_0(\mathbf x_N) \\ \vdots & \ddots & \vdots \\ \phi_{M-1}(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_N) \end{pmatrix}\begin{pmatrix} \boldsymbol{\phi}(\mathbf x_1)^\mathrm T \\ \vdots \\ \boldsymbol{\phi}(\mathbf x_N)^\mathrm T \end{pmatrix}\mathbf w \end{align} \]（基底が \( M \) 次元、観測データ（の個数）が \( N \) 次元）

（転置されていたりするが、同じ形の行列が何度も出てくるので名前を付ける。この(↓)形を）計画行列(design matrix) \( \boldsymbol \Phi \) とする\[ \boldsymbol\Phi = \begin{pmatrix} \boldsymbol\phi(\mathbf x_1)^\mathrm T \\ \vdots \\ \boldsymbol\phi(\mathbf x_N)^\mathrm T \end{pmatrix} = \begin{pmatrix} \phi_0(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_1) \\ \vdots & \ddots & \vdots \\ \phi_0(\mathbf x_N) & \cdots & \phi_{M-1}(\mathbf x_N) \end{pmatrix} \]（計画行列は \( N\times M \) 行列。\( N \) は観測の数、\( M \) は基底関数の次元数）

計画行列を用いる\[ \begin{align} \sum_{n=1}^Nt_n\boldsymbol\phi(\mathbf x_n) &= \sum_{n=1}^N\left( \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right)\boldsymbol\phi(\mathbf x_n) \\ ~~~ \begin{pmatrix} \phi_0(\mathbf x_1) & \cdots & \phi_0(\mathbf x_N) \\ \vdots & \ddots & \vdots \\ \phi_{M-1}(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_N) \end{pmatrix}\begin{pmatrix} t_1 \\ \vdots \\ t_n \end{pmatrix} &= \begin{pmatrix} \phi_0(\mathbf x_1) & \cdots & \phi_0(\mathbf x_N) \\ \vdots & \ddots & \vdots \\ \phi_{M-1}(\mathbf x_1) & \cdots & \phi_{M-1}(\mathbf x_N) \end{pmatrix}\begin{pmatrix} \boldsymbol{\phi}(\mathbf x_1)^\mathrm T \\ \vdots \\ \boldsymbol{\phi}(\mathbf x_N)^\mathrm T \end{pmatrix}\mathbf w ~~~ \\ \boldsymbol\Phi^\mathrm T\mathbf t &= \boldsymbol\Phi^\mathrm T\boldsymbol\Phi\mathbf w \end{align} \]（\( \mathbf t \) は目標ベクトル、\( \mathbf w \) は係数ベクトル）

パラメタ \( \mathbf w \) について解く（\( \mathbf w \) の最尤推定解）\[ \therefore \mathbf w_\mathrm{ML} = \left( \boldsymbol\Phi^\mathrm T\boldsymbol\Phi \right)^{-1}\boldsymbol\Phi^\mathrm T\mathbf t = \boldsymbol\Phi^\dagger\mathbf t \]（\( \boldsymbol\Phi^\dagger \) は計画行列の疑似逆行列。行列が退化（ランク落ち）してなければ求まる）

\( \beta \) について対数尤度を最大化する

対数尤度関数\[ ~~~ \ln p(\mathbf t|\mathbf w,\beta) = \frac{N}{2}\ln\beta - \frac{N}{2}\ln(2\pi) - \frac{\beta}{2}\sum_{n=1}^N\left\{ t_n - \mathbf w^\mathrm T\boldsymbol\phi(\mathbf x_n) \right\}^2 ~~~ \]

\( \beta \) について偏微分して \( 0 \) になるところ\[ \frac{\partial}{\partial\beta}\ln p(\mathbf t|\mathbf w, \beta) = \frac{N}{2\beta} - \frac{1}{2}\sum_{n=1}{N}\left\{ t_n - \mathbf w^\mathrm T\boldsymbol \phi(\mathbf x_n) \right\}^2 = 0 \]

\( \beta \) の最尤推定解\[ \therefore \frac{1}{\beta_\mathrm{ML}} = \frac{1}{N}\sum_{n=1}^N\left\{ t_n - \mathbf w_\mathrm{ML}^\mathrm T\boldsymbol\phi(\mathbf x_n) \right\}^2 \]

計画行列を用いて書けば\[ \therefore \frac{1}{\beta_\mathrm{ML}} = \frac{1}{N}(\boldsymbol\Phi\mathbf w_\mathrm{ML} - \mathbf t)^\mathrm T(\boldsymbol\Phi\mathbf w_\mathrm{ML} - \mathbf t) \]

多項式基底関数(polynomial basis function)の例。基底関数は \( \boldsymbol\phi(x) = (1, x, x^2, x^3)^\mathrm T \)

スクリプトと計算結果

OctaveR言語
%% observation
D = load("dataset1.txt");
x = D(:,1); t = D(:,2);

%% linear basis function
function retval = phi_0(x) % dummy
  retval = 1;
end

function retval = phi_1(x)
  retval = x;
end

function retval = phi_2(x)
  retval = x**2;
end

function retval = phi_3(x)
  retval = x**3;
end

%% design matrix
Phi = [phi_0(x(1)) phi_1(x(1)) phi_2(x(1)) phi_3(x(1))
       phi_0(x(2)) phi_1(x(2)) phi_2(x(2)) phi_3(x(2))
       phi_0(x(3)) phi_1(x(3)) phi_2(x(3)) phi_3(x(3))
       phi_0(x(4)) phi_1(x(4)) phi_2(x(4)) phi_3(x(4))
       phi_0(x(5)) phi_1(x(5)) phi_2(x(5)) phi_3(x(5))
       phi_0(x(6)) phi_1(x(6)) phi_2(x(6)) phi_3(x(6))
       phi_0(x(7)) phi_1(x(7)) phi_2(x(7)) phi_3(x(7))
       phi_0(x(8)) phi_1(x(8)) phi_2(x(8)) phi_3(x(8))
       phi_0(x(9)) phi_1(x(9)) phi_2(x(9)) phi_3(x(9))
       phi_0(x(10)) phi_1(x(10)) phi_2(x(10)) phi_3(x(10))];

%% maximum likelihood
w_ML = pinv(Phi)*t % (Phi'*Phi)^-1*Phi'*t
 
library(MASS)

## observation
D <- matrix(scan("dataset1.txt"), ncol=2, byrow=TRUE)
x <- D[,1]; my.t <- D[,2]

## linear basis function
phi_0 <- function(x) return(1) # dummy
phi_1 <- function(x) return(x)
phi_2 <- function(x) return(x^2)
phi_3 <- function(x) return(x^3)

## design matrix
Phi <- matrix(c(phi_0(x[1]), phi_0(x[2]), phi_0(x[3]), phi_0(x[4]), phi_0(x[5]), phi_0(x[6]),phi_0(x[7]), phi_0(x[8]), phi_0(x[9]), phi_0(x[10]),
                phi_1(x[1]), phi_1(x[2]), phi_1(x[3]), phi_1(x[4]), phi_1(x[5]), phi_1(x[6]),phi_1(x[7]), phi_1(x[8]), phi_1(x[9]), phi_1(x[10]),
                phi_2(x[1]), phi_2(x[2]), phi_2(x[3]), phi_2(x[4]), phi_2(x[5]), phi_2(x[6]),phi_2(x[7]), phi_2(x[8]), phi_2(x[9]), phi_2(x[10]),
                phi_3(x[1]), phi_3(x[2]), phi_3(x[3]), phi_3(x[4]), phi_3(x[5]), phi_3(x[6]),phi_3(x[7]), phi_3(x[8]), phi_3(x[9]), phi_3(x[10])),
              ncol=4)

## maximum likelihood
(w_ML <- ginv(Phi)%*%my.t) # solve(t(Phi)%*%Phi)%*%t(Phi)%*%my.t
 
> w_ML
w_ML =

   -0.070920
   12.040647
  -34.456121
   22.340354


> w_ML
             [,1]
[1,]  -0.07091998
[2,]  12.04064707
[3,] -34.45612073
[4,]  22.34035368

データセットは上記と同じものを使用。最尤解 \( \mathbf w_\mathrm{ML} \) が、最小二乗法で求めた解に一致することを確認

ベイズ線形回帰(Bayesian linear regression)

\( \mathbf w \) の事後分布 ← 尤度関数 \( \mathbf w_\mathrm{ML} \) × \( \mathbf w \) の事前分布

\( \beta \) は既知とする

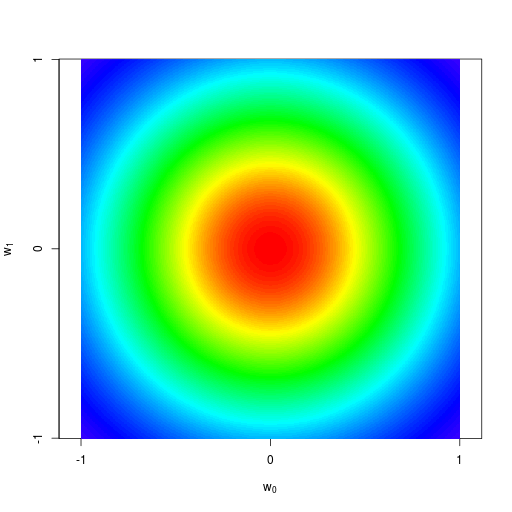
尤度関数\[ \begin{align} p(\mathbf{t}|\mathbf{w}) &= \prod_{n=1}^N\mathcal{N}(t_n|\mathbf{w}^\mathrm{T}\boldsymbol\phi(\mathbf x_n),\beta^{-1}) \\ &= \prod_{n=1}^N\frac{1}{\sqrt{2\pi\beta^{-1}}}\exp\left\{ -\frac{\beta}{2}\left(t_n - \mathbf{w}^\mathrm{T}\boldsymbol\phi(\mathbf x_n)\right)^2 \right\} \\ &= \frac{1}{(2\pi\beta^{-1})^{N/2}}\exp\left\{ -\frac{\beta}{2}\sum_{n=1}^N\left(t_n - \mathbf{w}^\mathrm{T}\boldsymbol\phi(\mathbf x_n)\right)^2 \right\} \\ &= \frac{1}{(2\pi\beta^{-1})^{N/2}}\exp\left\{ -\frac{\beta}{2}(\mathbf{t} - \mathbf{\Phi w})^\mathrm{T}(\mathbf{t} - \mathbf{\Phi w}) \right\} \\ &= \mathcal{N}(\mathbf{t}|\mathbf{\Phi w},\beta^{-1}\mathbf{I}) \end{align} \]（１次元のガウス分布のかけ算が、一つの多次元ガウス分布として書くことができる）

事前分布\[ p(\mathbf{w}) = \mathcal{N}(\mathbf{w}|\mathbf{m}_0,\mathbf{S}_0) \]（\( \mathbf m_0 \) と \( \mathbf S_0 \)（分布の中心と共分散）は事前の信念に従って適当に決める）

考えているモデル\[ \begin{align} p(\mathbf{w}) &= \mathcal{N}(\mathbf{w}|\mathbf{m}_0,\mathbf{S}_0) \\ p(\mathbf{t}|\mathbf{w}) &= \mathcal{N}(\mathbf{t}|\mathbf{\Phi w},\beta^{-1}\mathbf{I}) \end{align} \]に、ガウス分布の公式をあてはめる

事後分布\[ p(\mathbf w|\mathbf t)=\mathcal{N}(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N) \]（\( \mathbf m_N \) と \( \mathbf S_N \) は \( N \) 個のデータを観測した後に（ベイズ推定によって）更新された新たな信念）

パラメタ \( \mathbf m_N \) と \( \mathbf S_N \)\[ \begin{align} \mathbf{m}_N &= \mathbf{S}_N\left(\mathbf{S}_0^{-1}\mathbf{m}_0 + \beta\boldsymbol{\Phi}^\mathrm{T}\mathbf{t}\right) \\ \mathbf{S}_N^{-1} &= \mathbf{S}_0^{-1} + \beta\boldsymbol{\Phi}^\mathrm{T}\boldsymbol{\Phi} \end{align} \]

事前分布が \( 0 \) 中心で等方的なガウス分布の場合\[ \begin{align} \mathbf{m}_0 &= \mathbf{0} \\ \mathbf{S}_0 &= \alpha^{-1}\mathbf{I} \end{align} \]\[ \begin{align} \mathbf{m}_N &= \beta\mathbf{S}_N\boldsymbol\Phi^\mathrm{T}\mathbf{t} \\ \mathbf{S}_N^{-1} &= \alpha\mathbf{I} + \beta\boldsymbol\Phi^\mathrm{T}\boldsymbol\Phi \end{align} \]（ハイパーパラメータは \( \alpha \)、\( \beta \)（、パラメータは \( \mathbf w \)））

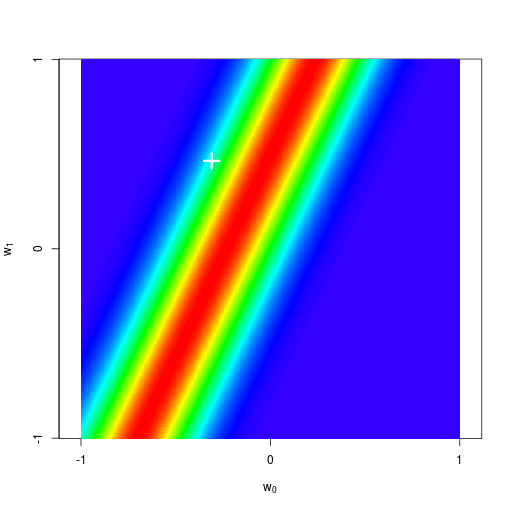
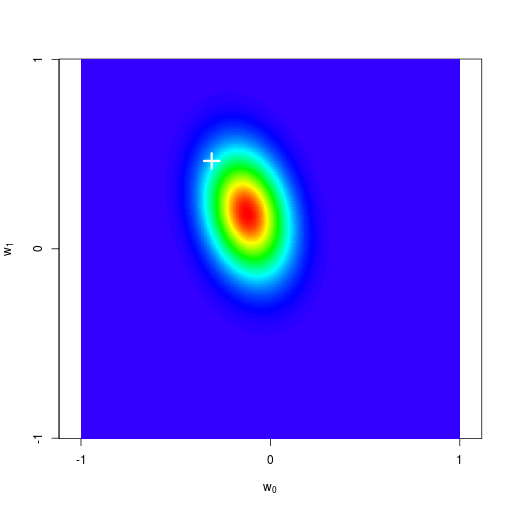
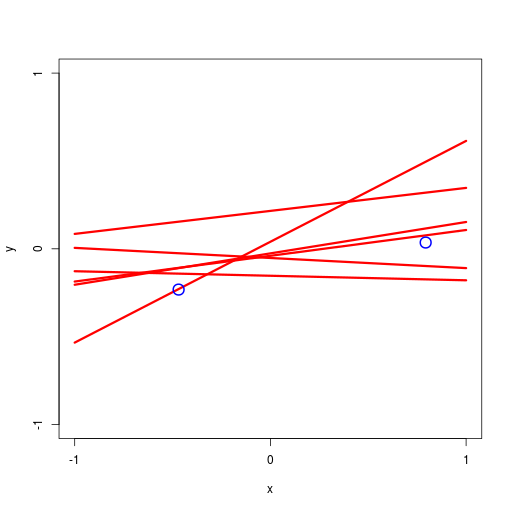
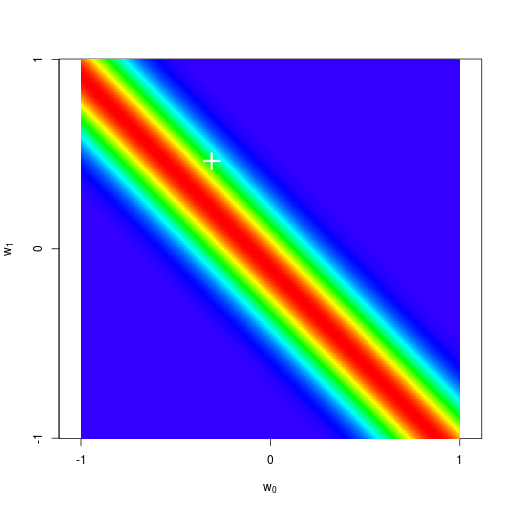
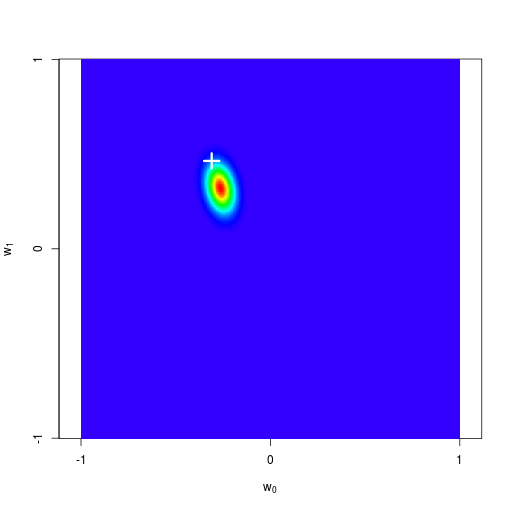
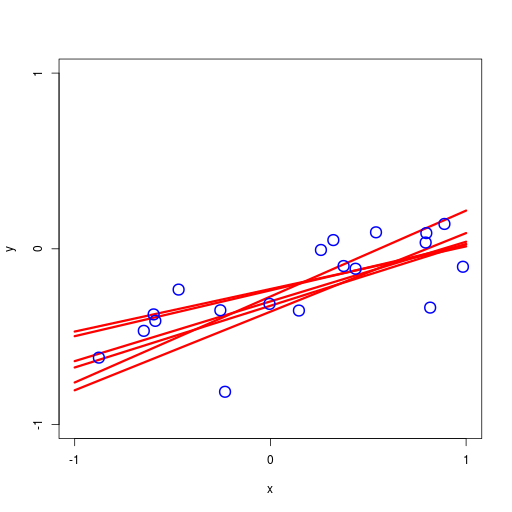
逐次ベイズ学習(sequential Bayesian learning)の例

priordata space
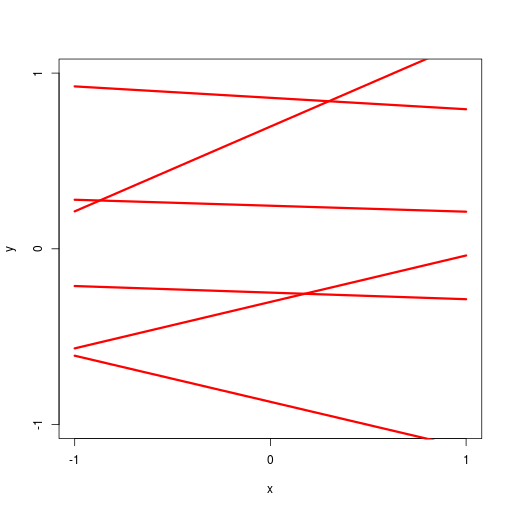likelihoodprior/posteriordata space

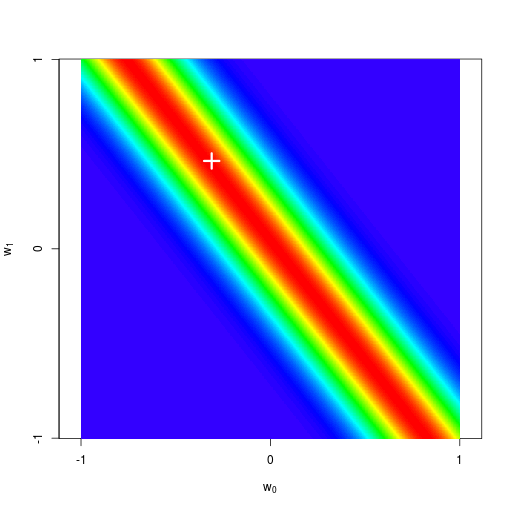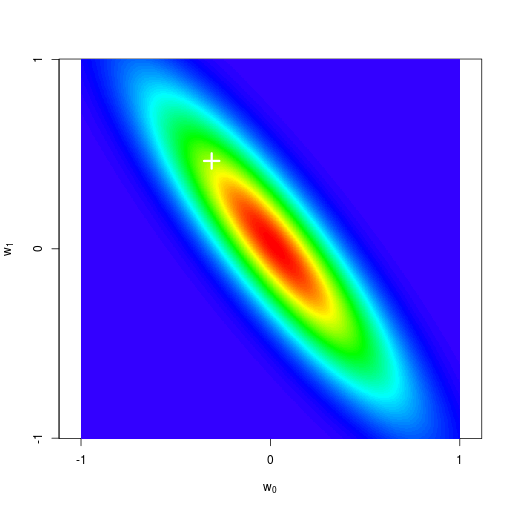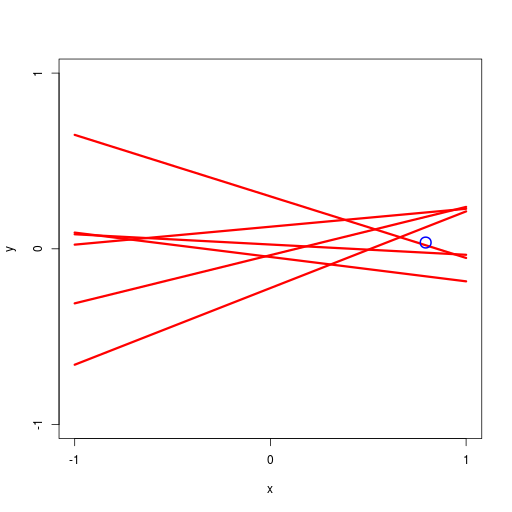ソースコード

R言語
library(mvtnorm)

set.seed(0)

## dataset
x <- runif(19, -1, 1)
y <- function(x, w) return(w[1] + w[2]*x)
D.t <- y(x, c(-0.3, 0.5)) + rnorm(length(x), 0, 0.2)

## hyper parameter
alpha <- 2.5
beta <- 25 # 1/0.2^2

## prior
m_0 <- c(0, 0)
S_0 <- alpha^-1*diag(2)

g.fileno = 1
visualize.parameter.space <- function(m, S, answer=FALSE) {
    png(paste("fig32-", g.fileno, ".png", sep=""), width=512, height=512); g.fileno <<- g.fileno + 1
    x <- y <- seq(-1, 1, len=512)
    z <- outer(x, y, function(x, y) dmvnorm(cbind(x, y), m, S))
    image(x, y, z, asp=1, xaxp=c(-1, 1, 2), yaxp=c(-1, 1, 2), xlab=expression(w[0]), ylab=expression(w[1]), col=rev(rainbow(100, end=.7)))
    if (answer) {
        par(new=TRUE)
        plot(-0.3, 0.5, xlim=c(-1, 1), ylim=c(-1, 1), xlab="", ylab="", axes=FALSE, cex=2, lwd=3, pch=3, col="white")
    }
    dev.off()
}

visualize.parameter.space(m_0, S_0)

visualize.data.space <- function(m, S, x=c(), my.t=c()) {
    png(paste("fig32-", g.fileno, ".png", sep=""), width=512, height=512); g.fileno <<- g.fileno + 1
    w <- rmvnorm(6, m, S)
    for (i in 1:dim(w)[1])
        plot(function(x) y(x, w[i,]), ylab="y", xlim=c(-1, 1), ylim=c(-1, 1), xaxp=c(-1, 1, 2), yaxp=c(-1, 1, 2), lwd=3, col="red", add=(i != 1))
    if (length(x) > 0 && length(my.t) > 0 && length(x) == length(my.t)) {
        par(new=TRUE)
        plot(x, my.t, xlim=c(-1, 1), ylim=c(-1, 1), xlab="", ylab="", axes=FALSE, cex=2, lwd=2, col="blue")
    }
    dev.off()
}

visualize.data.space(m_0, S_0)

visualize.parameter.space.likelihood <- function(my.t, Phi, S) {
    png(paste("fig32-", g.fileno, ".png", sep=""), width=512, height=512); g.fileno <<- g.fileno + 1
    x <- y <- seq(-1, 1, len=512)
    z <- outer(x, y) # adhoc
    for (i in 1:512) {
        for (j in 1:512) {
            w <- matrix(c(x[i], y[j]), ncol=1);
            z[i,j] <- dnorm(my.t, Phi%*%w, sqrt(S))
        }
    }
    image(x, y, z, asp=1, xaxp=c(-1, 1, 2), yaxp=c(-1, 1, 2), xlab=expression(w[0]), ylab=expression(w[1]), col=rev(rainbow(100, end=.7)))
    if (TRUE) { # answer
        par(new=TRUE)
        plot(-0.3, 0.5, xlim=c(-1, 1), ylim=c(-1, 1), xlab="", ylab="", axes=FALSE, cex=2, lwd=3, pch=3, col="white")
    }
    dev.off()
}

## linear basis function
phi_0 <- function(x) x^0 # rep(1, length(x))
phi_1 <- function(x) x

for (N in c(1, 2, length(D.t))) { # observation N
    my.t <- matrix(D.t[1:N], ncol=1)
    Phi <- matrix(c(phi_0(x[1:N]), phi_1(x[1:N])), ncol=2) # design matrix
    S_n <- solve(alpha*diag(2) + beta*t(Phi)%*%Phi)
    m_n <- beta*S_n%*%t(Phi)%*%my.t

    visualize.parameter.space.likelihood(my.t[N], Phi[N,], beta^-1)
    visualize.parameter.space(m_n, S_n, TRUE) # posterior
    visualize.data.space(m_n, S_n, x[1:N], my.t)
}

予測分布(predictive distribution)

実際には、通常 \( \mathbf w \) の値そのものには興味がなく、むしろ新しい \( \mathbf x\) の値に対する \( t \) を予測したい。そのためには、\[ p(t|\mathbf t) = \int p(t|\mathbf w)p(\mathbf w|\mathbf t)\,\mathrm d\mathbf w = \int\mathcal N(t|\mathbf w^\mathrm T\boldsymbol\phi(\mathbf x), \beta^{-1})\mathcal N(\mathbf w|\mathbf m_N, \mathbf S_N)\,\mathrm d\mathbf w \]で定義される予測分布を評価する必要がある

計算。予測分布\[ p(t|\mathbf t) = \int p(t|\mathbf w) p(\mathbf w|\mathbf t)\,\mathrm d\mathbf w \]\[ p(t|\mathbf w) = \mathcal N(t|\mathbf w^\mathrm T \boldsymbol\phi(\mathbf x), \beta^{-1}),\ p(\mathbf w|\mathbf t) = \mathcal N(\mathbf w|\mathbf m_N, \mathbf S_N) \]

ガウス分布の公式をあてはめる\[ \therefore p(t|\mathbf t) = \mathcal N(t|\mathbf m_N^\mathrm T \boldsymbol\phi(\mathbf x), \frac{1}{\beta} + \boldsymbol\phi(\mathbf x)^\mathrm T \mathbf S_N \boldsymbol\phi(\mathbf x)) \]

予測分布の平均 \( \mathbf m_N^\mathrm T \boldsymbol\phi(\mathbf x) \) は、MAP解に一致している（\( \mathbf w_\mathrm{MAP} = \mathbf m_N \)）

予測分布の分散は、既知とした精度 \( \beta \) の逆数（分散）に、\( \boldsymbol\phi(\mathbf x)^\mathrm T \mathbf S_N \boldsymbol\phi(\mathbf x) \) の項だけ足したものになっている（分散がその分だけ大きくなっている）

cf.

ベイズ推定の結果のMAP解\[ p(\mathbf w|\mathbf t)=\mathcal N(\mathbf w|\mathbf m_N, \mathbf S_N),\ \mathbf w_\mathrm{MAP} = \mathbf m_N \]

線形基底関数モデルの式\[ p(t|\mathbf w, \beta) = \mathcal N(t|\mathbf w^\mathrm T \boldsymbol\phi(\mathbf x), \beta^{-1}) \]\( \mathbf w \) にMAP解 \( \mathbf w_\mathrm{MAP} \) を採用\[ p(t|\mathbf w_\mathrm{MAP}, \beta) = \mathcal N(t|\mathbf w_\mathrm{MAP}^\mathrm T \boldsymbol\phi(\mathbf x), \beta^{-1}) = \mathcal N(t|\mathbf m_N^\mathrm T \boldsymbol\phi(\mathbf x), \beta^{-1}) \]

予測分布の例

予測分布と事後分布からサンプリングしたプロット

ソースコード

R言語
library(mvtnorm)

set.seed(0)

## dataset
D.x <- runif(25, 0, 1)
D.y <- function(x) sin(2*pi*x)
D.t <- D.y(D.x) + rnorm(length(D.x), 0, 0.3)

## hyper parameter
beta <- 25 # 1/0.2^2

## prior
m_0 <- matrix(rep(0, 9), ncol=1)
S_0 <- 2*diag(9)

## Gaussian basis function
mu <- seq(0, 1, len=9)
s <- 0.2
phi <- function(x, mu, s) exp(-(((x - mu)^2)/(2*s^2)))

for (N in 1:length(D.t)) { # observation N
    my.t <- matrix(D.t[1:N], ncol=1)
    my.x <- D.x[1:N]
    Phi <- matrix(c(phi(my.x, mu[1], s), phi(my.x, mu[2], s), phi(my.x, mu[3], s), phi(my.x, mu[4], s), phi(my.x, mu[5], s), phi(my.x, mu[6], s),
                    phi(my.x, mu[7], s), phi(my.x, mu[8], s), phi(my.x, mu[9], s)), ncol=9) # design matrix
    S_N <- solve(solve(S_0) + beta*t(Phi)%*%Phi)
    m_N <- S_N%*%(solve(S_0)%*%m_0 + beta*t(Phi)%*%my.t)

    if (TRUE) { # visualize
        png(paste("fig33-",formatC(N, width=2, flag="0"), ".png", sep=""), width=640, height=480)
        x <- seq(0, 1, len=1024)
        my.sd <- my.mean <- rep(0, 1024)
        for (i in 1:1024) {
            basis <- matrix(c(phi(x[i], mu[1], s), phi(x[i], mu[2], s), phi(x[i], mu[3], s), phi(x[i], mu[4], s), phi(x[i], mu[5], s), phi(x[i], mu[6], s),
                              phi(x[i], mu[7], s), phi(x[i], mu[8], s), phi(x[i], mu[9], s)), ncol=1)
            my.mean[i] <- t(m_N)%*%basis
            my.sd[i] <- sqrt(beta^-1 + t(basis)%*%S_N%*%basis)
        }
        plot(NULL, main=paste("N =", N), xlab="x", ylab="t", xlim=c(0, 1), ylim=c(-1.5, 1.5), axes=FALSE)
        polygon(c(x, rev(x)), c(my.mean + my.sd, rev(my.mean - my.sd)), col="#ffd9d9", border=NA)
        lines(x, my.mean, lwd=3, col="red")
        points(my.x, my.t, cex=2, lwd=3, col="blue")
        lines(x, D.y(x), lwd=3, col="green")
        box(); axis(side=1, at=c(0, 1)); axis(side=2, at=c(-1, 0, 1))
        dev.off()
    }

    if (TRUE) { # visualize
        png(paste("fig34-",formatC(N, width=2, flag="0"), ".png", sep=""), width=640, height=480)
        x <- seq(0, 1, len=1024)
        for (i in 1:5) {
            w <- rmvnorm(1, m_N, S_N)
            y <- (w[1]*phi(x, mu[1], s) + w[2]*phi(x, mu[2], s) + w[3]*phi(x, mu[3], s) + w[4]*phi(x, mu[4], s) + w[5]*phi(x, mu[5], s) + w[6]*phi(x, mu[6], s)
                + w[7]*phi(x, mu[7], s) + w[8]*phi(x, mu[8], s) + w[9]*phi(x, mu[9], s))
            if (i == 1)
                plot(x, y, main=paste("N =", N), xlab="x", ylab="t", xlim=c(0, 1), ylim=c(-1.5, 1.5), xaxp=c(0, 1, 1), yaxp=c(-1, 1, 2), type="l", lwd=2, col="red")
            else
                lines(x, y, lwd=2, col="red")
            if (N == 1)
                lines(x, D.y(x), lwd=3, col="green")
            points(my.x, my.t, cex=2, lwd=3, col="blue")
        }
        dev.off()
    }
}

if (FALSE) { # animation
    system("convert -delay 100 -loop 0 fig33-*.png fig33.gif")
    system("convert -delay 100 -loop 0 fig34-*.png fig34.gif")
}

ベイズモデル比較、エビデンス近似

モデル選択、モデルエビデンスなど

《積み残し》

教科書

© 2020 Tadakazu Nagai