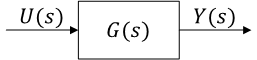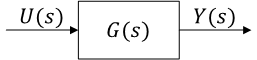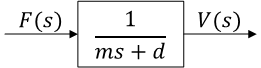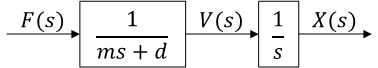制御理論
永井 忠一 2021.2.6
ラプラス変換(Laplace transform)
定義\[ X(s) = \mathcal{L}\left[ x(t) \right] = \int_0^\infty x(t)e^{-st} dt \](\( s \) をラプラス演算子(Laplace operator)と言う)
(Maxima によるラプラス変換の計算)例
| Maxima |
|---|
単位インパルス関数(ディラックのデルタ関数)
(unit impulse function)\[ \mathcal{L}\left[ \delta(t) \right] \] |
(%i1) laplace(delta(t), t, s);
\[ 1 \] |
| 単位ステップ関数(unit step function)\[ \mathcal{L}\left[ 1 \right] \] |
(%i2) laplace(1, t, s);
\[ {{1}\over{s}} \] |
| 単位ランプ関数(unit ramp function)\[ \mathcal{L}\left[ t \right] \] |
(%i3) laplace(t, t, s);
\[ {{1}\over{s^2}} \] |
| 指数関数\[ \mathcal{L}\left[ e^{-at} \right] \] |
(%i4) laplace(%e^(-a*t), t, s);
\[ {{1}\over{s+a}} \] |
| 微分\[ \mathcal{L}\left[ \frac{d}{dt} x(t) \right] \] |
(%i5) laplace(diff(x(t), t), t, s);
\[ s\,\mathcal{L}\left(x\left(t\right) , t , s\right)-x\left(0\right) \] |
| 積分\[ \mathcal{L}\left[ \int_0^t x(\tau) d\tau \right] \] |
(%i6) laplace(integrate(x(\\tau), \\tau, 0, t), t, s);
\[ {{\mathcal{L}\left(x\left(t\right) , t , s\right)}\over{s}} \] |
(Maxima の tex() 関数で計算結果を TEX の式に変換)
性質
| 線形性 | \[ \mathcal L[af(t) + bg(t)] = aF(s) + bG(s) \] |
|---|
| 合成積、畳み込み積分(convolution)\[ \left( f(t)*g(t) = \int_{-\infty}^\infty f(\tau)g(t - \tau)d\tau \right) \] | \[ \mathcal L\left[ \int_0^t f(t - \tau)g(\tau) d\tau \right] = F(s)G(s) \]\[ \mathcal L\left[ f(t)*g(t) \right] = F(s)G(s) \] |
|---|
微分
(\( x^{(n)} \) は \( n \) 階導関数) | \[ \mathcal L\left[f^{(n)}(t)\right] = s^nF(s) - s^{n - 1}f(0) - s^{n -2}f'(0) - \cdots - sf^{(n - 2)}(0) - f^{(n - 1)}(0) \] |
|---|
| (\( s \) 領域での)移動定理 | \[ \mathcal L[f(t)e^{at}] = F(s - a) \] |
|---|
| (\( t \) 領域での)移動定理 | \[ \mathcal L[f(t - \tau)] = e^{-\tau s}F(s) \] |
|---|
| 最終値の定理 | \[ \lim_{t\to\infty} f(t) = \lim_{s\to 0} sF(s) \] |
|---|
伝達関数(transfer function)とブロック線図(block diagram)
\( Y(s) = G(s)U(s) \) のブロック線図
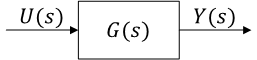 |
- \( U(s) \) : 入力
- \( Y(s) \) : 出力
- \( G(s) \) : 伝達関数
|
入力 \( U(s) \) と出力 \( Y(s) \) の比が伝達関数\[ G(s) = \frac{ Y(s) }{ U(s) } \]
等価変換
| Octave | Scilab |
|---|
| 直列接続(series connection)\[ G(s) = G_2(s)G_1(s) \] | octave:1> pkg load control
octave:2> G1 = tf([1], [10 0 0])
Transfer function 'G1' from input 'u1' to output ...
1
y1: ------
10 s^2
Continuous-time model.
octave:3> G2 = tf([1 1], [1 2])
Transfer function 'G2' from input 'u1' to output ...
s + 1
y1: -----
s + 2
Continuous-time model.
octave:4> G = series(G1, G2)
Transfer function 'G' from input 'u1' to output ...
s + 1
y1: ---------------
10 s^3 + 20 s^2
Continuous-time model.
octave:5> G = G2*G1
Transfer function 'G' from input 'u1' to output ...
s + 1
y1: ---------------
10 s^3 + 20 s^2
Continuous-time model.
| --> G1 = 1/(10*%s^2)
G1 =
1
----
10s²
--> G2 = (%s + 1)/(%s + 2)
G2 =
1 +s
----
2 +s
--> G = G2*G1
G =
1 +s
----------
20s² +10s³
|
|---|
| 並列接続(parallel connection)\[ G(s) = G_1(s) + G_2(s) \] | octave:6> G = parallel(G1, G2)
Transfer function 'G' from input 'u1' to output ...
10 s^3 + 10 s^2 + s + 2
y1: -----------------------
10 s^3 + 20 s^2
Continuous-time model.
octave:7> G = G1 + G2
Transfer function 'G' from input 'u1' to output ...
10 s^3 + 10 s^2 + s + 2
y1: -----------------------
10 s^3 + 20 s^2
Continuous-time model.
| --> G = G1 + G2
G =
2 +s +10s² +10s³
----------------
20s² +10s³
|
|---|
| フィードバック接続(feedback connection)\[ W(s) = \frac{ G(s)H(s) }{ 1 + G(s)H(s) } \] | octave:8> G = tf([2 5 1], [1 2 3])
Transfer function 'G' from input 'u1' to output ...
2 s^2 + 5 s + 1
y1: ---------------
s^2 + 2 s + 3
Continuous-time model.
octave:9> H = tf([5 10], [1 10])
Transfer function 'H' from input 'u1' to output ...
5 s + 10
y1: --------
s + 10
Continuous-time model.
octave:10> W = feedback(G, H)
Transfer function 'W' from input 'u1' to output ...
2 s^3 + 25 s^2 + 51 s + 10
y1: ---------------------------
11 s^3 + 57 s^2 + 78 s + 40
Continuous-time model.
| --> G = (2*%s^2 + 5*%s + 1)/(%s^2 + 2*%s + 3)
G =
1 +5s +2s²
----------
3 +2s +s²
--> H = (5*%s + 10)/(%s + 10)
H =
10 +5s
------
10 +s
--> W = G/.H
W =
10 +51s +25s² +2s³
-------------------
40 +78s +57s² +11s³
|
|---|
(Scilab では、「%s」は多項式の変数。「/.」はフィードバック演算子)
Octave の control パッケージのインストール(私の環境では Linux apt)
| Linux apt |
|---|
$ sudo apt install octave-control
|
直結フィードバックシステム
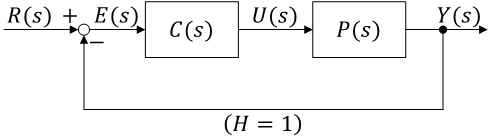 |
- \( P(s) \) : 制御対象(plant, process)
- \( C(s) \) : 制御器(controller)
- \( R(s) \) : 参照値(reference)
- \( Y(s) \) : 出力
- \( E(s) \) : 偏差(error)
- \( U(s) \) : 制御出力
|
(フィードバック経路に伝達関数が存在しない \( \left( H = 1 \right) \))
偏差 \( E(s) \) は \( R(s) - Y(s)\)(ネガティブ・フィードバック(negative feedback))
ブロック線図の基本要素:矢印は信号の流れを表し、黒丸 • の引き出し点(branch point)で信号の分岐を表し、白丸 ○ の加算点(summing point)で信号の和を表す(加減算を入ってくる矢印の符号 ± で表す。注意としては、加算点に入ってくる信号は単位が等しくなければならない)
フィードバックシステムの伝達関数を Octave と Scilab で求める
| Octave | Scilab |
|---|
octave:1> pkg load control
octave:2> P = tf([2 5 1], [1 2 3])
Transfer function 'P' from input 'u1' to output ...
2 s^2 + 5 s + 1
y1: ---------------
s^2 + 2 s + 3
Continuous-time model.
octave:3> C = tf([5 10], [1 10])
Transfer function 'C' from input 'u1' to output ...
5 s + 10
y1: --------
s + 10
Continuous-time model.
octave:4> W = feedback(series(C, P), 1)
Transfer function 'W' from input 'u1' to output ...
10 s^3 + 45 s^2 + 55 s + 10
y1: ---------------------------
11 s^3 + 57 s^2 + 78 s + 40
Continuous-time model.
| --> P = (2*(%s)^2 + 5*(%s) + 1)/(%s^2 + 2*(%s) + 3)
P =
1 +5s +2s²
----------
3 +2s +s²
--> C = (5*(%s) + 10)/(%s + 10)
C =
10 +5s
------
10 +s
--> W = (P*C)/.(1)
W =
10 +55s +45s² +10s³
-------------------
40 +78s +57s² +11s³
|
力学システムの表現
以下の力学システムを考える
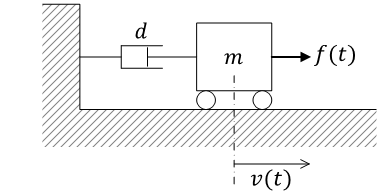 |
- \( m \) : 質量
- \( d \) : ダンパー係数(粘性摩擦係数)
|
運動方程式\[ m\frac{ dv(t) }{ dt } + dv(t) = f(t) \]
運動方程式をラプラス変換する\[ m\left( sV(s) - v(0) \right) + dV(s) = F(s) \]
初期値を \( v(0) = 0 \) とすると\[ (ms + d)v(s) = f(s) \]
伝達関数とブロック線図
一次遅れ系となる
出力 \( V(s) \) を積分すれば位置 \( X(s) \)。積分は \( \boxed{ \frac{1}{s} } \)
伝達関数をまとめると\[ F(s)\longrightarrow\boxed{ \frac{ 1 }{ ms^2 + ds } }\longrightarrow X(s) \]となる
もう一つの例。次に、以下の MSD システム(mass-spring-damper system)を考える
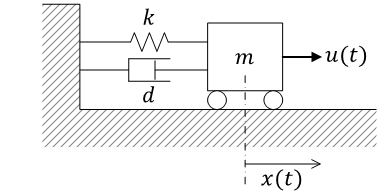 |
- \( m \) : 質量
- \( k \) : ばね定数
- \( d \) : ダンパー係数(粘性摩擦係数)
|
\( u(t) \) はシステムへの入力で、力 \( f \)。位置(変位)\( x(t) \) が、システムの出力となる
運動方程式\[ m\ddot x + d\dot x + kx = f \]
運動方程式をラプラス変換する\[ m\left\{ s^2X(s) - sx(0) - \dot x(0) \right\} + d\left\{ sX(s) -x(0) \right\} + kX(s) = F(s) \]位置の初期値 \( x(0) = 0 \)、速度の初期を \( \dot x(0) = 0 \) とすると\[ \left( ms^2 + ds + k \right)X(s) = F(s) \]
伝達関数\[ P(s) = \frac{1}{ms^2 + ds + k} = \frac{ X(s) }{ F(s) } \]2次遅れ系となる
ブロック線図
Maxima を使って、運動方程式をラプラス変換して伝達関数を求める
| Maxima |
|---|
(%i1) laplace(m*diff(x(t), t, 2) + d*diff(x(t), t) + k*x(t) = f(t), t, s);
\[ m\,\left(-\left.{{d}\over{d\,t}}\,x\left(t\right)\right|_{t=0}+s^2
\,\mathcal{L}\left(x\left(t\right) , t , s\right)-x\left(0\right)\,s
\right)+d\,\left(s\,\mathcal{L}\left(x\left(t\right) , t , s\right)-
x\left(0\right)\right)+k\,\mathcal{L}\left(x\left(t\right) , t , s
\right)=\mathcal{L}\left(f\left(t\right) , t , s\right) \] |
(%i1) atvalue(x(t), t = 0, 0);
(%o1) 0
(%i2) atvalue(diff(x(t), t), t = 0, 0);
(%o2) 0
(%i3) laplace(m*diff(x(t), t, 2) + d*diff(x(t), t) + k*x(t) = f(t), t, s);
\[ m\,s^2\,\mathcal{L}\left(x\left(t\right) , t , s\right)+d\,s\,
\mathcal{L}\left(x\left(t\right) , t , s\right)+k\,\mathcal{L}\left(
x\left(t\right) , t , s\right)=\mathcal{L}\left(f\left(t\right) , t
, s\right) \](%i4) solve(%, laplace(x(t), t, s))/laplace(f(t), t, s);
\[ \left[ {{\mathcal{L}\left(x\left(t\right) , t , s\right)}\over{
\mathcal{L}\left(f\left(t\right) , t , s\right)}}={{1}\over{m\,s^2+d
\,s+k}} \right] \] |
atvalue() 関数で、初期位置と初期速度の初期条件 \( 0 \) を与える
電子回路とのアナロジーについて
(RLC 回路の例など)《積み残し》
システムの時間応答
上記の MSD システムの例\[ m\ddot x(t) + d\ddot x(t) + kx(t) = f(t) \xrightarrow{\mathcal L} (ms^2 + ds + k)X(s) = F(s) \]を考える。伝達関数とブロック線図\[ U(s) \longrightarrow \boxed{G(s) = \frac{1}{ms^2 + ds + k}} \longrightarrow Y(s)\]
係数を適当にとり(物理的なイメージは無し)、伝達関数が\[ G(s) = \frac{4}{s^2 + 3s + 2} \]と具体的に与えられた場合、このシステムの応答を計算する
単位インパルス応答(unit impulse response)
入力が単位インパルス関数。\( U(s) = \mathcal L\left[ \delta(t) \right] = 1 \)\[ \begin{align} Y(s) &= G(s)U(s) \\ &= G(s)\cdot 1 \\ &= G(s) \\ &= \frac{4}{s^2 + 3s + 2} \end{align} \]
単位ステップ応答(unit step response)
(教科書によっては、ステップ応答はインディシャル応答とも言う)
入力が単位ステップ関数。\( U(s) = \mathcal L[1] = \frac{1}{s} \)\[ Y(s) = G(s)U(S) = \frac{4}{s^2 + 3s + 2}\cdot\frac{1}{s} \]
逆ラプラス変換(inverse Laplace transform)
(ラプラス逆変換とも)\[ x(t) = \mathcal L^{-1}\left[ X(s) \right] \]
※計算せず、ラプラス変換表を参照してラプラス変換対を調べる
部分分数展開(partial fraction expansion)
(部分分数分解とも)
※手計算する場合には、「Heaviside の展開定理」を使うと(係数比較法よりも)簡単に係数が求められる
例)\( Y(s) = \frac{4}{s^2 + 3s + 2} \)
| Maxima | Octave |
|---|
(%i1) partfrac(4/(s^2 + 3*s + 2), s);
\[ {{4}\over{s+1}}-{{4}\over{s+2}} \] |
octave:1> [r,p,k] = residue([4], [1 3 2])
r =
4
-4
p =
-1
-2
k = [](0x0)
|
留数(residue)。residue() 関数の戻り値の意味:\( \frac{r_1}{s - p_1} + \frac{r_2}{s-p_2} + \cdots + \frac{r_n}{s-p_n} + k(s) \)
答え\[ y(t) = 4e^{-t} - 4e^{-2t} \xleftarrow{\mathcal L^{-1}} Y(s) = {{4}\over{s+1}}-{{4}\over{s+2}} = \frac{4}{s^2 + 3s + 2} \]
Maxima による逆ラプラス変換
| Maxima |
|---|
(%i1) ilt(4/(s^2 + 3*s + 2), s, t);
\[ 4\,e^ {- t }-4\,e^ {- 2\,t } \] |
例)\( Y(s) = \frac{4}{s^2 + 3s + 2}\frac{1}{s} \)
| Maxima | Octave |
|---|
(%i1) partfrac((4/(s^2 + 3*s + 2))*(1/s), s);
\[ {{2}\over{s+2}}-{{4}\over{s+1}}+{{2}\over{s}} \] |
octave:1> [r,p,k] = residue([4], conv([1 3 2], [1 0]))
r =
2.0000
-4.0000
2.0000
p =
0
-1
-2
k = [](0x0)
|
答え\[ y(t) = 2e^{-2t} - 4e^{-t} + 2 \xleftarrow{\mathcal L^{-1}} Y(s) = {{2}\over{s+2}}-{{4}\over{s+1}}+{{2}\over{s}} = \frac{4}{s^2 + 3s + 2}\frac{1}{s} \]
Maxima による逆ラプラス変換
| Maxima |
|---|
(%i1) ilt((4/(s^2 + 3*s + 2))*(1/s), s, t);
\[ -4\,e^ {- t }+2\,e^ {- 2\,t }+2 \] |
インパルス応答とステップ応答のシミュレーション
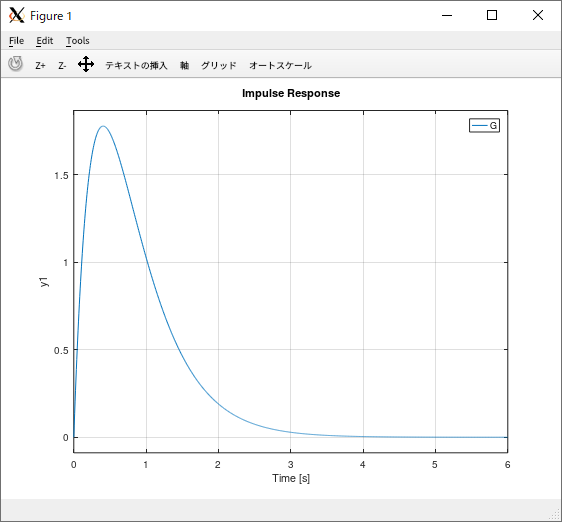
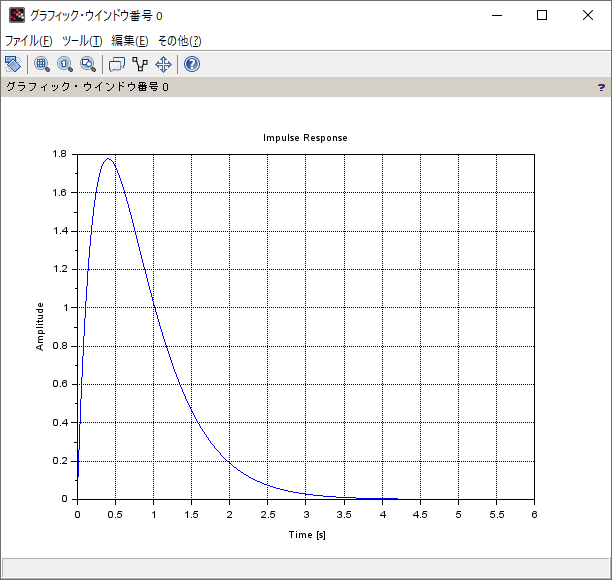
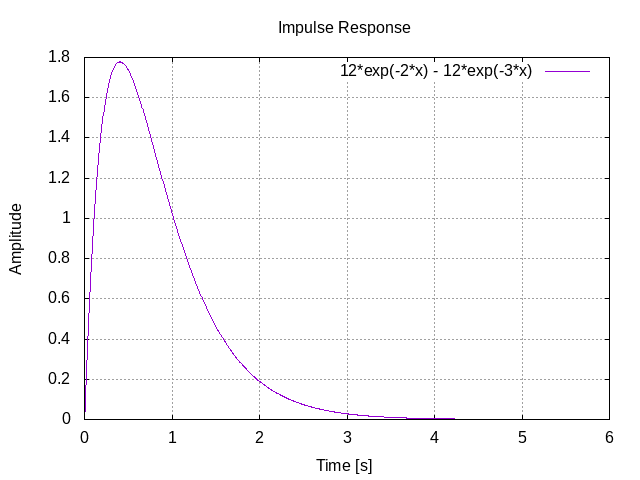
与えられている伝達関数\[ G(s) = \frac{12}{s^2 + 5s + 6} \]に対し、インパルス応答とステップ応答を求める
インパルス応答
| Octave | Scilab |
|---|
octave:1> pkg load control
octave:2> G = tf([12], [1 5 6])
Transfer function 'G' from input 'u1' to output ...
12
y1: -------------
s^2 + 5 s + 6
Continuous-time model.
octave:3> impulse(G, linspace(0, 6, 1024))
|
--> t = linspace(0, 6, 1024);
--> G = 12/(%s^2 + 5*(%s) + 6)
G =
12
---------
6 +5s +s²
--> y = csim('impulse', t, syslin('c', G));
--> plot(t, y); xgrid(); xtitle('Impulse Response', 'Time [s]', 'Amplitude')
|
実行結果
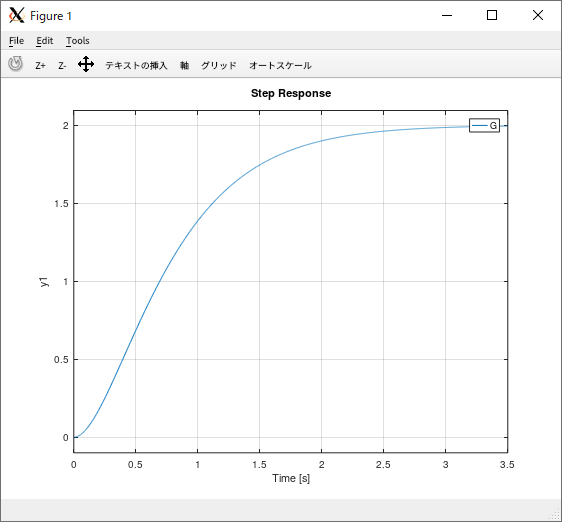
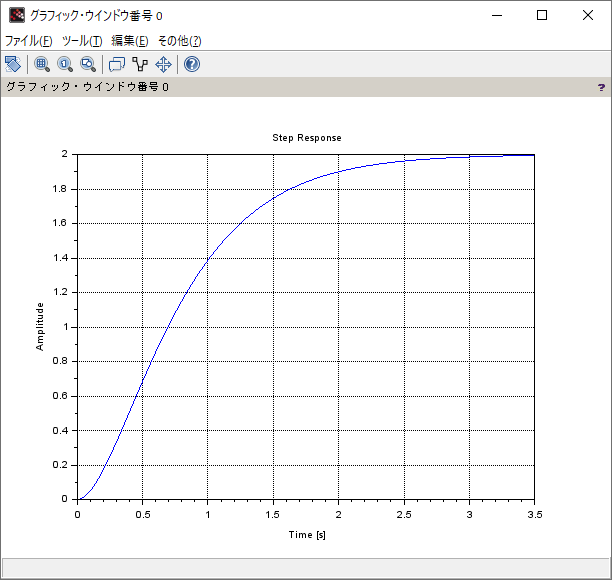
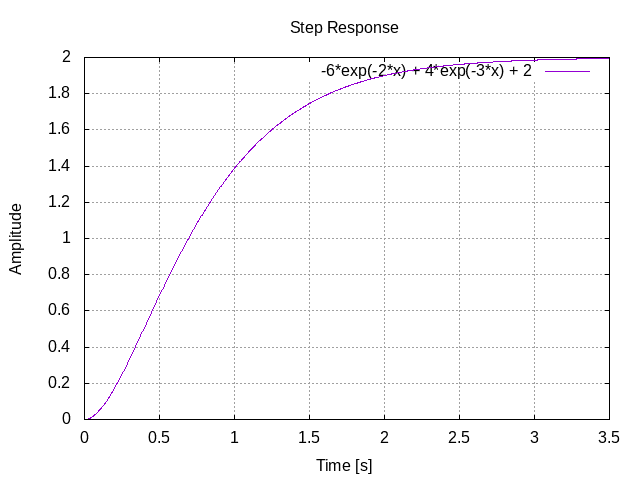
ステップ応答
| Octave(つづき) | Scilab(つづき) |
|---|
octave:4> step(G, linspace(0, 3.5, 1024))
|
--> clf()
--> t = linspace(0, 3.5, 1024);
--> y = csim('step', t, syslin('c', G));
--> plot(t, y); xgrid(); xtitle('Step Response', 'Time [s]', 'Amplitude')
|
実行結果
解析的に求めた結果との比較
| Maxima |
|---|
(%i1) ilt((12/(s^2 + 5*s + 6))*1, s, t);
\[ 12\,e^ {- 2\,t }-12\,e^ {- 3\,t } \](%i2) fortran(%);
12*exp(-2*t)-12*exp(-3*t)
(%o2) done
(%i3) ilt((12/(s^2 + 5*s + 6))*(1/s), s, t);
\[ -6\,e^ {- 2\,t }+4\,e^ {- 3\,t }+2 \](%i4) fortran(%);
(-6*exp(-2*t))+4*exp(-3*t)+2
(%o4) done
|
(Maxima の fortran() 関数で計算結果をプログラミング言語の式に変換。「%」は、直前のコマンドの実行結果を表す)
グラフツールによるプロット
| gnuplot |
|---|
gnuplot> set terminal png size 640,480
Terminal type is now 'png'
Options are 'nocrop enhanced size 640,480 font "arial,12.0" '
gnuplot> set output 'fig_impulse_response.png'
gnuplot> set title 'Impulse Response'
gnuplot> set xlabel 'Time [s]'
gnuplot> set ylabel 'Amplitude'
gnuplot> set grid
gnuplot> set xrange [0:6]
gnuplot> set sample 1024
gnuplot> plot 12*exp(-2*x) - 12*exp(-3*x)
gnuplot> set output 'fig_step_response.png'
gnuplot> set title 'Step Response'
gnuplot> set xrange [0:3.5]
gnuplot> plot -6*exp(-2*x) + 4*exp(-3*x) + 2
|
実行結果
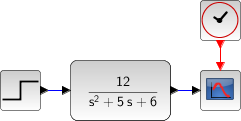
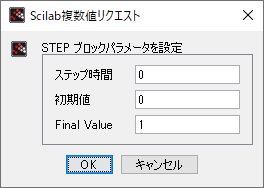
Xcos によるステップ応答のシミュレーション
Xcos では、伝達関数をそのまま扱うことができる
考えているシステムのブロック線図\[ u = 1 \longrightarrow \boxed{ \frac{12}{s^2 + 5s + 6} } \longrightarrow y \]
Xcos プログラム
各パレットの設定
シミュレーションの設定
「シミュレーション」メニュー → 「設定」
 |
シミュレーション結果
過渡応答(transient response)
1次遅れ要素
(first order lag element) |
1階線形微分方程式で表現される\[ T\frac{dy(t)}{dt} + y(t) = Ku(t) \]
- \( T \) : 時定数(time constant)
- \( K \) : 定常ゲイン(steady state gain)
伝達関数\[ G(s) = \frac{Y(s)}{U(s)} = \frac{K}{Ts + 1} \]
ステップ応答\[ Y(s) = \frac{K}{s(Ts + 1)} = \frac{K}{s} - \frac{KT}{Ts + 1} \xrightarrow{\mathcal L^{-1}} y(t) = K(1 - e^{-t/T}) \]
|
積分要素
(integral process) |
伝達関数\[ G(s) = \frac{K}{s} \]
ステップ応答\[ Y(s) = \frac{K}{s^2} \xrightarrow{\mathcal L^{-1}} y(t) = Kt \]
|
2次遅れ要素
(second order lag element) |
2階線形微分方程式で表現される\[ \tau^2\frac{d^2y(t)}{dt^2} + 2\zeta\tau\frac{dy(t)}{dt} + y(t) = Ku(t) \]
- \( \tau \) : 時定数(time constant)
- \( \zeta \) : 減衰係数(damping factor)、減衰比(damping ratio)
- \( K \) : 定常ゲイン(steady state gain)
伝達関数\[ G(s) = \frac{Y(s)}{U(s)} = \frac{K}{\tau^2s^2 + 2\zeta\tau s + 1} \]
伝達関数の分母多項式 \( = 0 \) として得られる方程式\[ \tau s^2 + 2\zeta\tau s + 1 = 0 \]を特性方程式(characteristic equation)と呼ぶ。特性方程式の根(特性根(characteristic root)と呼ぶ)\[ p_1 = \frac{-\zeta + \sqrt{\zeta^2 - 1}}{\tau},\ p_2 = \frac{-\zeta - \sqrt{\zeta^2 - 1}}{\tau} \]を極(pole)と呼ぶ。(以下、教科書の式より)
\( \zeta > 1 \) のとき
(overdamping process) |
伝達関数\[ G(s) = \frac{K}{\tau^2(s - p_1)(s - p_2)} = \frac{K}{(T_1 s + 1)(T_2 s + 1)} \]ステップ応答\[ y(t) = K\left( 1 - \frac{T_1}{T_1 - T_2}e^{-t/T_1} + \frac{T_2}{T_1 - T_2}e^{-t/T_2} \right) \] |
\( \zeta = 1 \) のとき
(critical damping process) |
伝達関数\[ G(s) = \frac{K}{(\tau s + 1)^2} \]ステップ応答\[ y(t) = K\left\{ 1 - \left( 1 + \frac{t}{\tau} \right)e^{-t/\tau} \right\} \] |
\( 0 < \zeta < 1 \) のとき
(underdamping process) |
伝達関数\[ Y(s) = \frac{K}{s(\tau^2 s^2 + 2\zeta\tau s + 1)} \](ステップ応答は伝達関数を逆ラプラス変換する)《省略》 |
(\( \zeta = 0 \) のとき:持続振動)
|
むだ時間要素
(delay process/dead time process) |
次式のような時間的な遅れを持つプロセス\[ c_o(t) = c_i(t - L) \]
- \( L \) : むだ時間(dead time)
伝達関数\[ G(s) = \frac{C_o(s)}{C_i(s)} = e^{-Ls}\]
ステップ応答\[ y(t) = u(t - L) \]
(「伝達関数 \( e^{-Ls} \) は時間を \( L \) だけ遅らせる演算子である」と考える)
|
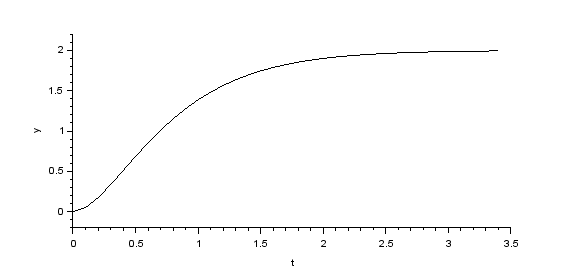
1次遅れ+むだ時間要素
(first order plus time delay; FOPTD) |
ブロック線図\[ U \longrightarrow \boxed{\frac{K}{Ts + 1}} \longrightarrow \boxed{e^{-Ls}} \longrightarrow Y\]
伝達関数\[ P(s) = \frac{K}{Ts + 1}e^{-Ls} \]
ステップ応答\[ y(t) = Ku^*(1 - e^{-(t - L)/T}) \]
|
(逆応答(inverse response)について)《積み残し》
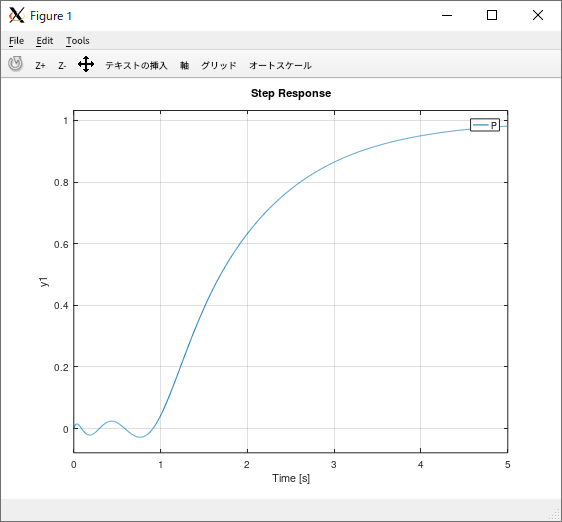
Xcos による「1次遅れ+むだ時間」シミュレーション
Xcos プログラム
パレットの設定
シミュレーション結果
パデ近似(Padé approximation)
むだ時間要素 \( e^{-Ls}\) を有理関数で近似(むだ時間 1.0 [s] 、次数4の例)
| Octave |
|---|
octave:1> pkg load control
octave:2> [num,den] = padecoef(1, 4)
num =
1.0000 -20.0000 180.0000 -840.0000 1680.0000
den =
1.0000 20.0000 180.0000 840.0000 1680.0000
octave:3> D = tf(num, den)
Transfer function 'D' from input 'u1' to output ...
s^4 - 20 s^3 + 180 s^2 - 840 s + 1680
y1: -------------------------------------
s^4 + 20 s^3 + 180 s^2 + 840 s + 1680
Continuous-time model.
octave:4> G = tf(1, [1 1])
Transfer function 'G' from input 'u1' to output ...
1
y1: -----
s + 1
Continuous-time model.
octave:5> P = D*G
Transfer function 'P' from input 'u1' to output ...
s^4 - 20 s^3 + 180 s^2 - 840 s + 1680
y1: -------------------------------------------------
s^5 + 21 s^4 + 200 s^3 + 1020 s^2 + 2520 s + 1680
Continuous-time model.
octave:6> step(P, linspace(0, 5, 1024))
|
実行結果
(※高次遅れ要素とむだ時間要素を区別することは難しい)
1次遅れ系のステップ応答の評価
プログラム
| Scilab |
|---|
K = 1; T = 1;
P = syslin('c', K/(T*(%s) + 1));
t = linspace(0, 4, 1024);
y = csim('step', t, P);
clf()
plot2d(t, y, axesflag=1)
xgrid(), xtitle('1st-order system', 't/T', 'y/K')
plot(t, (K/T)*t, '-.b')
plot(t, K*ones(t), '-.b')
mtlb_axis([0, 4, 0, 1.2])
t = [1 3];
y = csim('step', t, P);
scatter(t, y);
plot([0, t(1)], [y(1), y(1)], '--r')
plot([0, t(2)], [y(2), y(2)], '--r')
|
実行結果
(横軸 \(t/T\)、縦軸 \( y/K \) として無次元化)
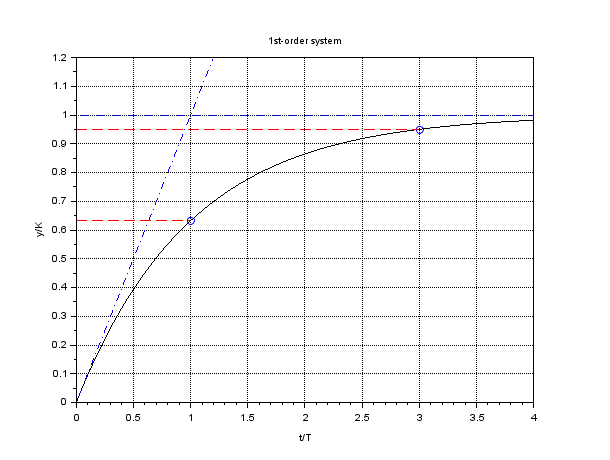 |
時刻 \( t = T \)(時定数)で出力が目標値の(およそ)63.2%(\( = 100(1 - e^{-1})\))に達する
\( T \)、\( 2T \)、\( 3T \) の時点を計算。プログラムと実行結果
| Octave |
|---|
pkg load control
P = tf(1, [1 1]);
y = step(P, [0 1 2 3]);
disp(y(2:4));
|
0.63212
0.86466
0.95021
|
2次遅れ系のステップ応答の評価
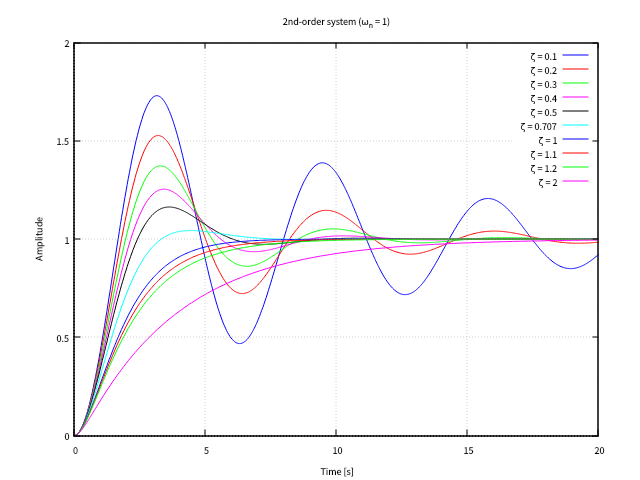
固有周波数(natural frequency) \( \omega_n \) を用いた伝達関数の一般形\[ G(s) = \frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2} \](\( \omega_n \) : 固有周波数(固有角周波数)、\( \zeta \) : 減衰係数)
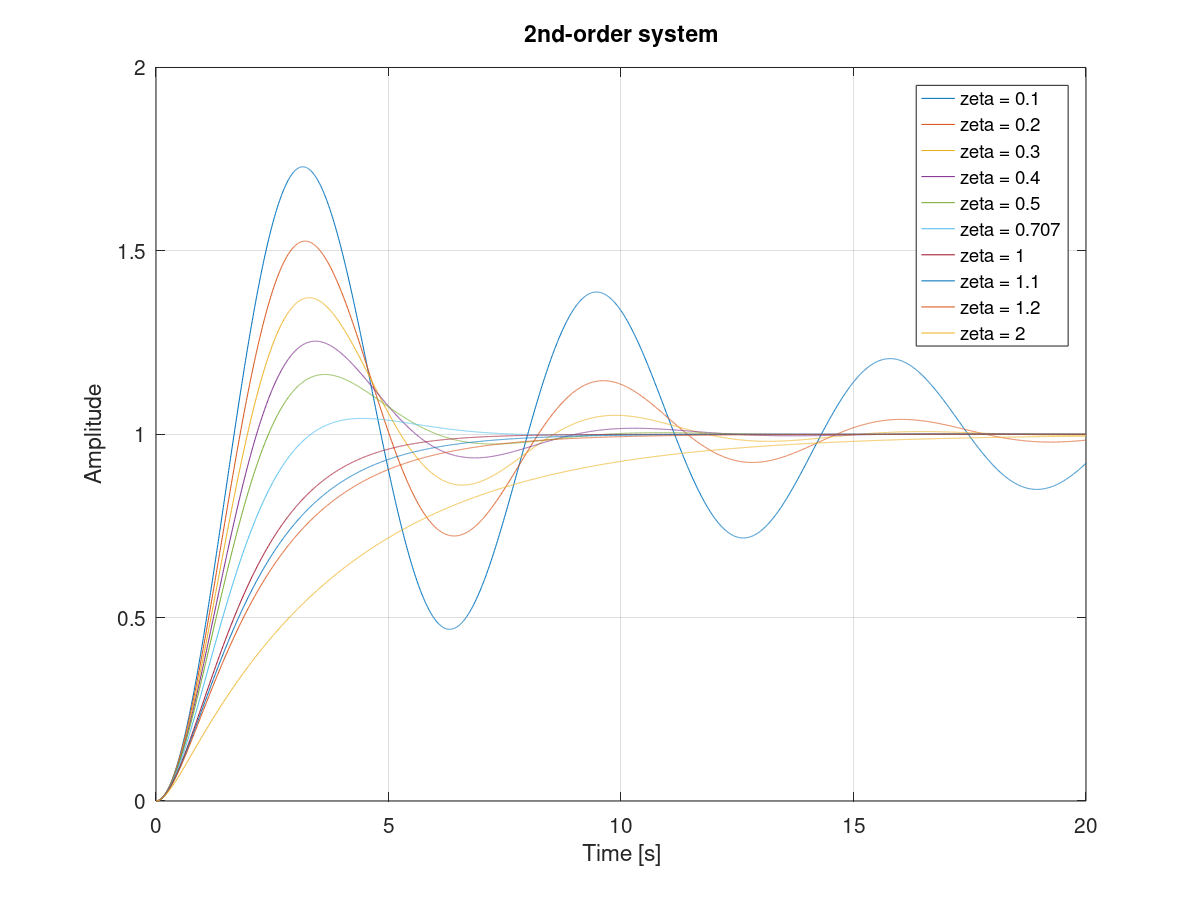
ステップ応答の計算プログラム(\( \omega_n = 1 \))
| Octave |
|---|
pkg load control
t = linspace(0, 20, 2048);
omega_n = 1;
for zeta = [0.1 0.2 0.3 0.4 0.5 0.707 1 1.1 1.2 2]
G = tf(omega_n^2, [1 2*zeta*omega_n omega_n^2]);
y = step(G, t);
plot(t, y)
hold on
end
grid on
legend('zeta = 0.1', 'zeta = 0.2', 'zeta = 0.3', 'zeta = 0.4', 'zeta = 0.5', 'zeta = 0.707', 'zeta = 1', 'zeta = 1.1', 'zeta = 1.2', 'zeta = 2')
title('2nd-order system'), xlabel('Time [s]'), ylabel('Amplitude')
|
実行結果
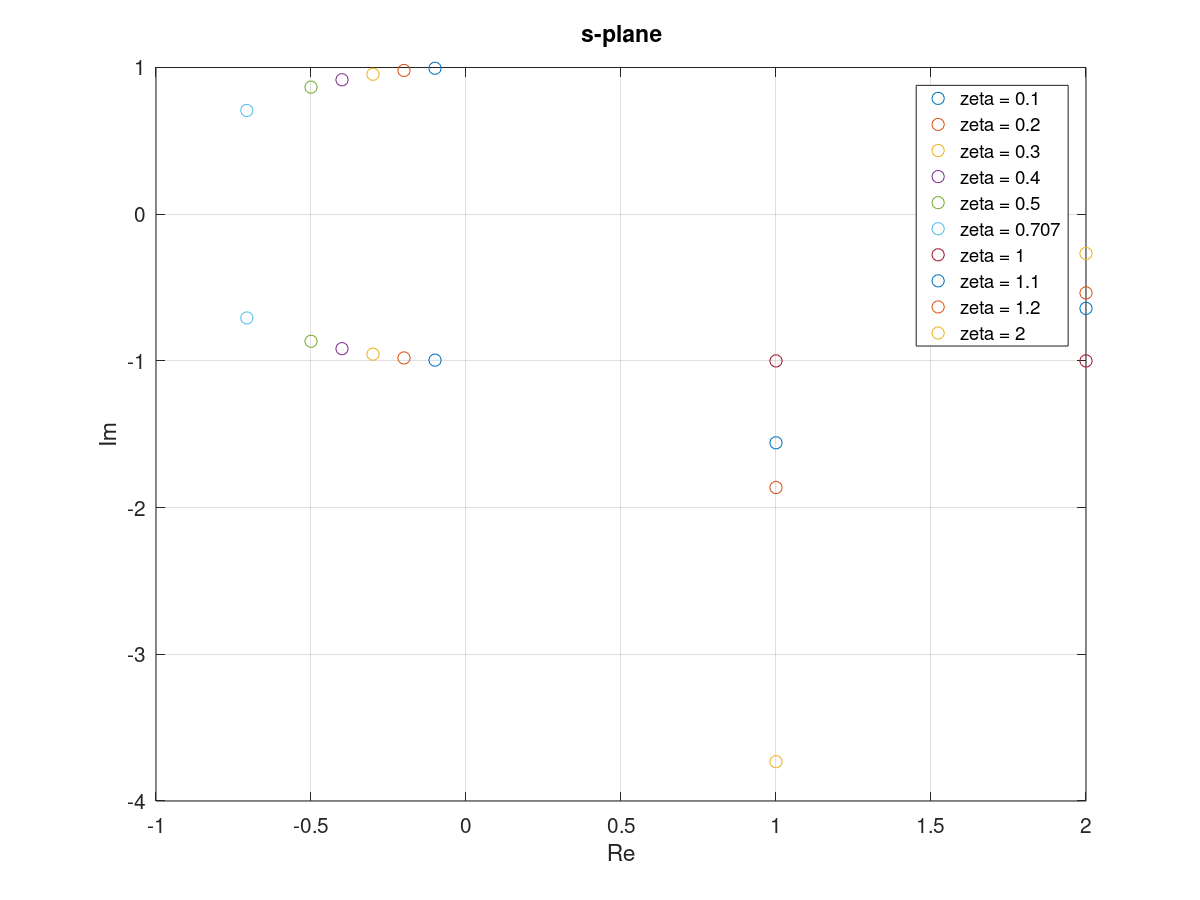
複素平面上(\( s \) 領域)で極(pole)の位置を確認
| Octave(つづき) |
|---|
clf
for zeta = [0.1 0.2 0.3 0.4 0.5 0.707 1 1.1 1.2 2]
plot(roots([1 2*zeta*omega_n omega_n^2]), 'o')
hold on
end
grid on
legend('zeta = 0.1', 'zeta = 0.2', 'zeta = 0.3', 'zeta = 0.4', 'zeta = 0.5', 'zeta = 0.707', 'zeta = 1', 'zeta = 1.1', 'zeta = 1.2', 'zeta = 2')
title('s-plane'), xlabel('Re'), ylabel('Im')
|
実行結果
2次遅れ系の性質
極は
| Maxima |
|---|
(%i1) solve(s^2 + 2*\\zeta*\\omega[n]*s + \\omega[n] = 0, s);
\[ \left[ s=-\sqrt{{\it \zeta}^2\,{\it \omega}_{n}^2-{\it \omega}_{n}}
-{\it \zeta}\,{\it \omega}_{n} , s=\sqrt{{\it \zeta}^2\,{\it \omega}
_{n}^2-{\it \omega}_{n}}-{\it \zeta}\,{\it \omega}_{n} \right] \] |
で与えられる
ステップ応答は\[ f(t) = \mathcal\ L^{-1}\left[ \frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2} \frac{1}{s} \right] \]で求められる
減衰係数 \( \zeta \) の値で場合分け
固有周波数 \( \omega_n = 1 \) として求める
| Maxima |
|---|
過制動、過減衰 \( \zeta > 1\)
(overdamping) | (%i1) G(\\zeta) := \\omega_n^2/(s^2 + 2*\\zeta*\\omega_n*s + \\omega_n^2);
2
\omega_n
(%o1) G(\zeta) := -----------------------------------
2 2
s + 2 \zeta \omega_n s + \omega_n
(%i2) \\omega_n: 1;
(%o2) 1
(%i3) U: 1/s;
1
(%o3) -
s
(%i4) assume(\\zeta > 1);
(%o4) [\zeta > 1]
(%i5) ilt(G(\\zeta)*U, s, t);
\[ e^ {- {\it \zeta}\,t }\,\left(-{{{\it \zeta}\,\sinh \left(\sqrt{
{\it \zeta}^2-1}\,t\right)}\over{\sqrt{{\it \zeta}^2-1}}}-\cosh
\left(\sqrt{{\it \zeta}^2-1}\,t\right)\right)+1 \](%i6) forget(\\zeta > 1);
(%o6) [\zeta > 1]
|
|---|
臨界制動、臨界減衰 \( \zeta = 1\)
(critical damping) | (%i7) assume(equal(\\zeta, 1));
(%o7) [equal(\zeta, 1)]
(%i8) ilt(G(\\zeta)*U, s, t);
\[ \left(-{\it \zeta}\,t-1\right)\,e^ {- {\it \zeta}\,t }+1 \](%i9) forget(equal(\\zeta, 1));
(%o9) [equal(\zeta, 1)]
|
|---|
不足制動 \( 0 < \zeta < 1\)
(underdamping) | (%i10) assume(0 < \\zeta, \\zeta < 1);
(%o10) [\zeta > 0, \zeta < 1]
(%i11) ilt(G(\\zeta)*U, s, t);
\[ e^ {- {\it \zeta}\,t }\,\left(-{{{\it \zeta}\,\sin \left(\sqrt{1-
{\it \zeta}^2}\,t\right)}\over{\sqrt{1-{\it \zeta}^2}}}-\cos \left(
\sqrt{1-{\it \zeta}^2}\,t\right)\right)+1 \](%i12) forget(0 < \\zeta, \\zeta < 1);
(%o12) [\zeta > 0, \zeta < 1]
|
|---|
\( \zeta \) の値が \( 0 < \zeta < 1\) の範囲において、得られた逆ラプラス変換の式に三角関数が含まれていることから、ステップ応答が振動的な挙動となること分かる(減衰振動)
得られた(Maxima による記号計算で求めた)一般解の式に対して、\( \zeta \) に具体的な値を代入して応答のグラフを描画
| Maxima |
|---|
(%i1) \\omega_n: 1$
(%i2) G(\\zeta) := \\omega_n^2/(s^2 + 2*\\zeta*\\omega_n*s + \\omega_n^2)$
(%i3) U: 1/s$
(%i4) assume(\\zeta > 1)$
(%i5) define(f_od(\\zeta, t)/* overdamping */, ilt(G(\\zeta)*U, s, t))$
(%i6) forget(\\zeta > 1)$ assume(equal(\\zeta, 1))$
(%i8) define(f_cd(\\zeta, t)/* critical damping */, ilt(G(\\zeta)*U, s, t))$
(%i9) forget(equal(\\zeta, 1))$ assume(0 < \\zeta, \\zeta < 1)$
(%i11) define(f_ud(\\zeta, t)/* underdamping */, ilt(G(\\zeta)*U, s, t))$
(%i12) my_f: [f_ud(0.1, t), f_ud(0.2, t), f_ud(0.3, t), f_ud(0.4, t), f_ud(0.5, t), f_ud(0.707, t), f_cd(1, t), f_od(1.1, t), f_od(1.2, t), f_od( 2, t)]$
(%i13) my_legend: [legend, "{/Symbol z} = 0.1", "{/Symbol z} = 0.2", "{/Symbol z} = 0.3", "{/Symbol z} = 0.4", "{/Symbol z} = 0.5", "{/Symbol z} = 0.707", "{/Symbol z} = 1", "{/Symbol z} = 1.1", "{/Symbol z} = 1.2", "{/Symbol z} = 2"]$
(%i14) plot2d(my_f, [t, 0, 20], [y, 0, 2], [xlabel, "Time [s]"], [ylabel, "Amplitude"], [title, "2nd-order system ({/Symbol w}_n = 1)"], my_legend, grid2d);
|
実行結果
ラウスの安定判別法(Routh criteria)
(※手計算の方法は教科書などを参照)《省略》
特性方程式\[ s^4 + 2s^3 + 3s^2 + 4s + 5 = 0 \]をもつシステムの安定性を調べる(例には、物理的なイメージ無し)
ラウス表(Routh table)を作成する
| Scilab |
|---|
--> cp = %s^4 + 2*(%s)^3 + 3*(%s)^2 + 4*(%s) + 5 // characteristic polynomial
cp =
5 +4s +3s² +2s³ +s⁴
--> [rt, num] = routh_t(cp) // Routh table
rt =
1. 3. 5.
2. 4. 0.
1. 5. 0.
-6. 0. 0.
5. 0. 0.
num =
2.
|
ラウス表(の第1列)のラウス数列(Routh series)に着目する
| Scilab |
|---|
--> rs = rt(:,1) // Routh series
rs =
1.
2.
1.
-6.
5.
|
システムが安定であるための必要十分条件は、ラウス数列の要素がすべて同符号であること。この例では、符号が「1 → -6」と「-6 → 5」の2回変化している(システムは不安定)
不安定根の数は、ラウス数列における正負の符号変化の数に等しい
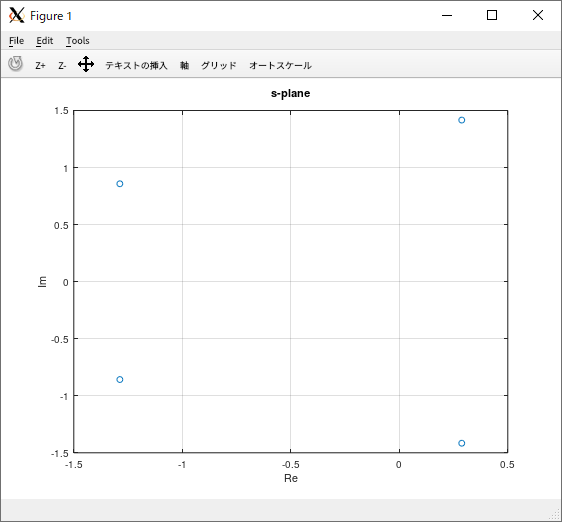
| Octave |
|---|
octave:1> roots([1 2 3 4 5])
ans =
-1.28782 + 0.85790i
-1.28782 - 0.85790i
0.28782 + 1.41609i
0.28782 - 1.41609i
octave:2> plot(ans, 'o'), title('s-plane'), xlabel('Re'), ylabel('Im'), grid on
|
(Octave では、変数「ans」に直前の実行結果が格納される)
確認結果(複素平面の右半平面にある2つの根が不安定根)
(BIBO 安定(bounded input, bounded output stability)について)《積み残し》
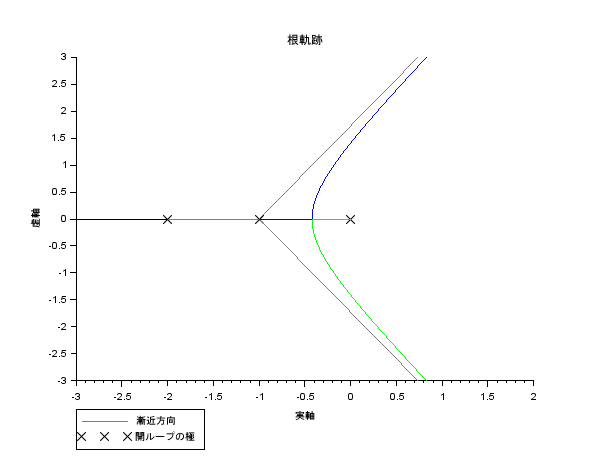
根軌跡(root locus)
(根軌跡法、根軌跡解析)
一巡伝達関数が\[ L(s) = \frac{K}{s(s + 1)(s + 2)} \]であるフィードバック制御系
 |
- \( L \) : 一巡伝達関数(open-loop transfer function)
|
(比例制御システム)を考える
閉ループ伝達関数(closed-loop transfer function)
| Maxima |
|---|
(%i1) L: K/(s*(s + 1)*(s + 2));
K
(%o1) -----------------
s (s + 1) (s + 2)
(%i2) ratsimp(L/(1 + L));
K
(%o2) -------------------
3 2
s + 3 s + 2 s + K
|
特性方程式\[ s^3 + 3s^2 + 2s + K = 0 \]
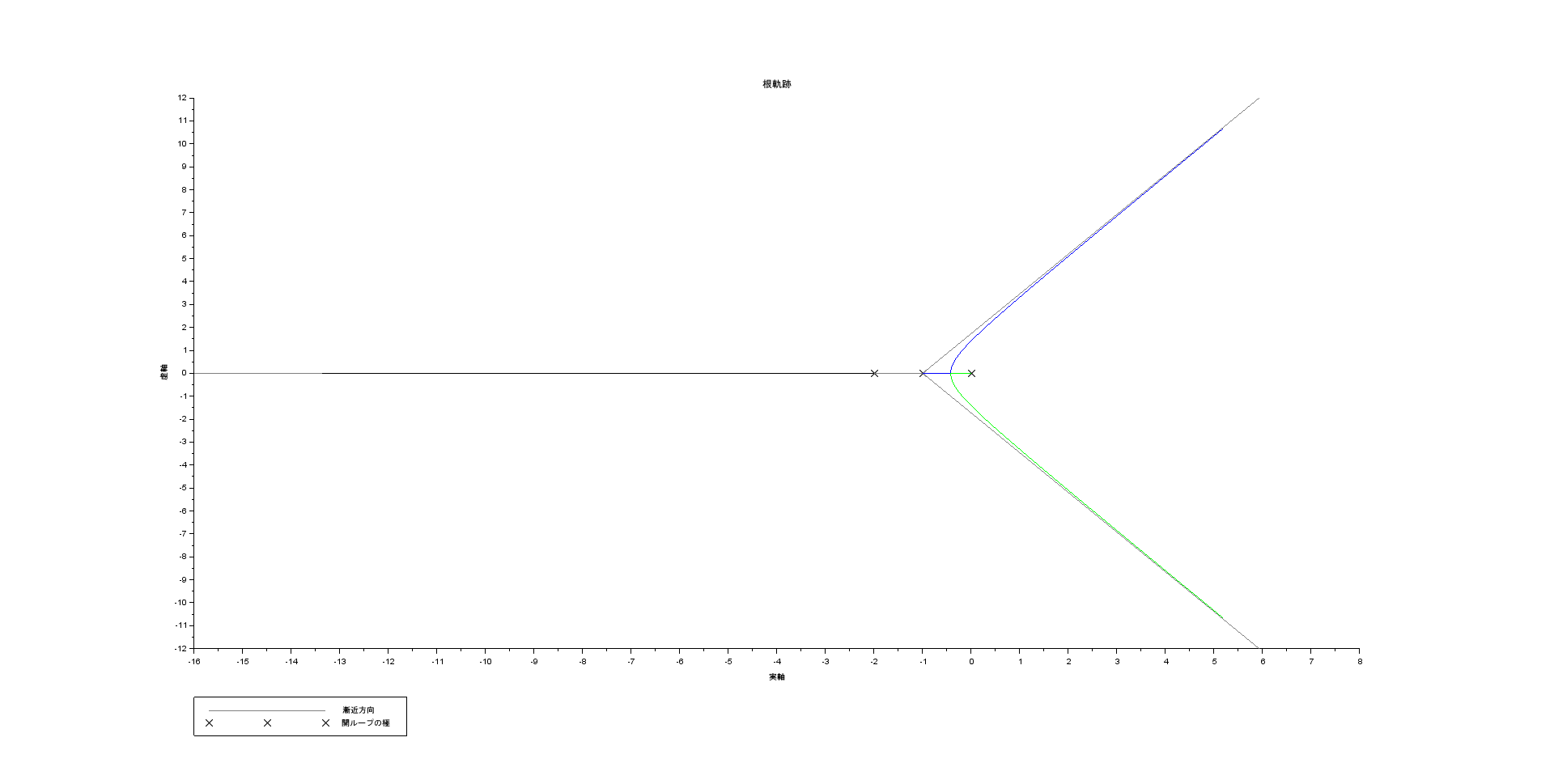
根軌跡(ゲイン \( K \) を \( 0 \) から \( \infty \) まで変化させたときの特性根の軌跡)を描く(ゲインのみが異なるシステムの根軌跡は同じになる)
Scilab の evans() 関数を利用
| Scilab |
|---|
--> num = 1; den = %s*(%s + 1)*(%s + 2);
--> L = syslin('c', num/den)
L =
1
-----------
2s +3s² +s³
--> evans(L)
--> mtlb_axis([-3 2 -3 3]);
--> kpure(num/den)
ans =
6.0000000
|
Scilab で根軌跡を描画
表示範囲を調整
また、Scilab では、kpure() 関数で「安定限界ゲイン」を求めることもできる
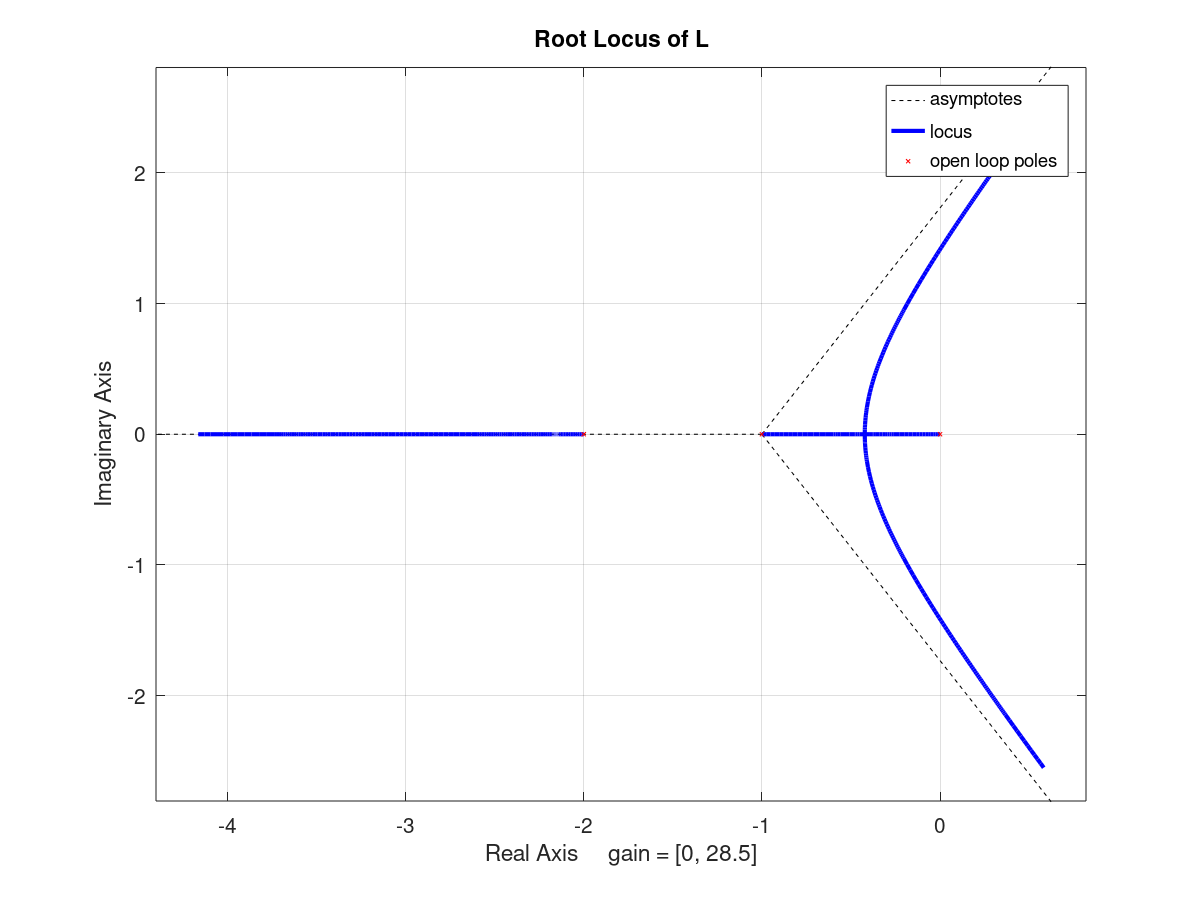
同じシステムについて、Octave の rlocus() 関数を利用して根軌跡を描画
| Octave |
|---|
octave:1> pkg load control
octave:2> L = tf(1, [1 0])*tf(1, [1 1])*tf(1, [1 2])
Transfer function 'L' from input 'u1' to output ...
1
y1: -----------------
s^3 + 3 s^2 + 2 s
Continuous-time model.
octave:3> rlocus(L)
|
Octave で描画した根軌跡
(詳細はメカトロニクスの教科書などを参照)
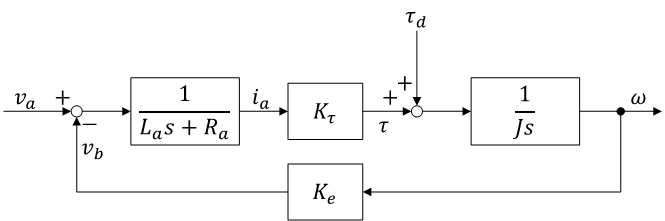
DC motor の等価回路
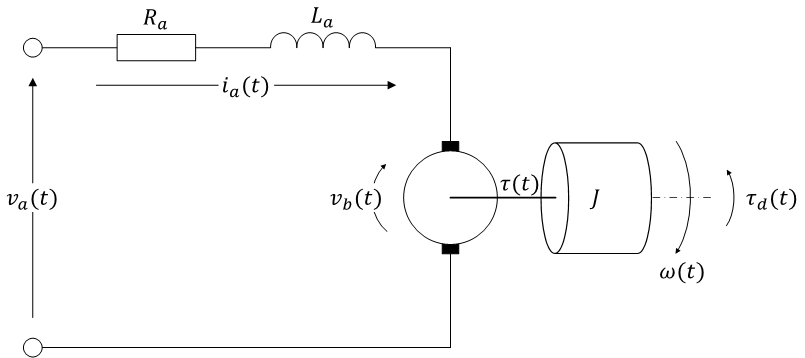 |
- 電機子(armature)回路
- \( v_a \) : 端子電圧
- \( R_a \) : 電機子抵抗
- \( L_a \) : 電機子インダクタンス(\( L_a \) の値は小さく \( 0 \) と仮定できることが多い)
- \( v_b \) : 逆起電力
(motor に流れる電流 \( i_a \)(電機子電流)に比例(\( K_\tau i_a \))したトルク \(\tau\) が発生する )
- 機械系
- \( \tau \) : トルク
- \( J \) : 慣性モーメント
- \( \omega \) : 角速度
- \( \tau_d\) : 外乱トルク(負荷トルク)
(ここでは、粘性抵抗、ばね項は考えない)「⇒ 粘性摩擦を考慮する場合」
(motor が回転すると角速度に比例(\( K_e\omega \))した逆起電力 \( v_b \) が発生する)
|
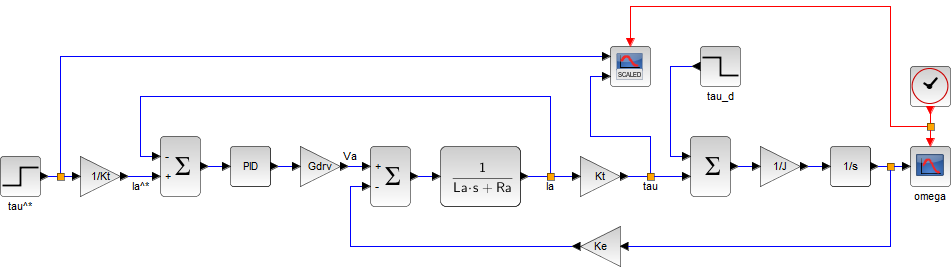
入力を電圧 \( v_a\)、出力を角速度 \( \omega \) として伝達関数を求める
DC motor のブロック線図(導出は教科書など)
(出力 \( \omega \) をさらに積分 \( \boxed{\frac{1}{s}} \) すれば角度 \( \theta \) となる)
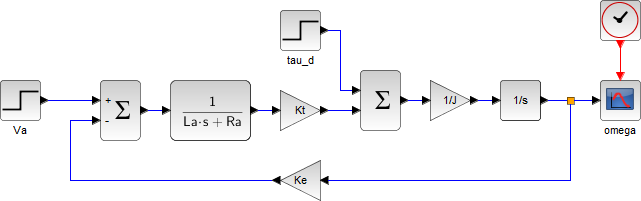
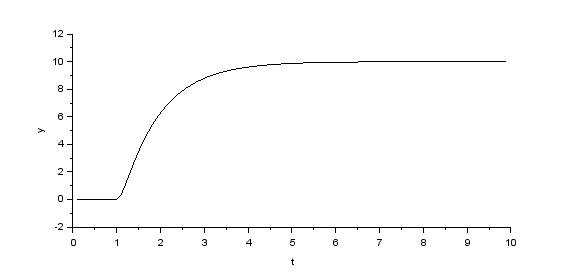
Xcos による DC motor のモデリング(演習)
各定数の値は適当。インダクタンスは小さいとする。\( K_\tau \) と \( K_e \) は、同じ値になる(フレミングの左手の法則と右手の法則)
| Scilab |
|---|
--> Ra = 1; La = 0.1; J = 1; Kt = 1; Ke = Kt;
--> tau_d = 0;
--> Va = 10;
|
(Xcos のプログラムはこちら)
シミュレーション結果
| \( \omega \) |
|---|
 |
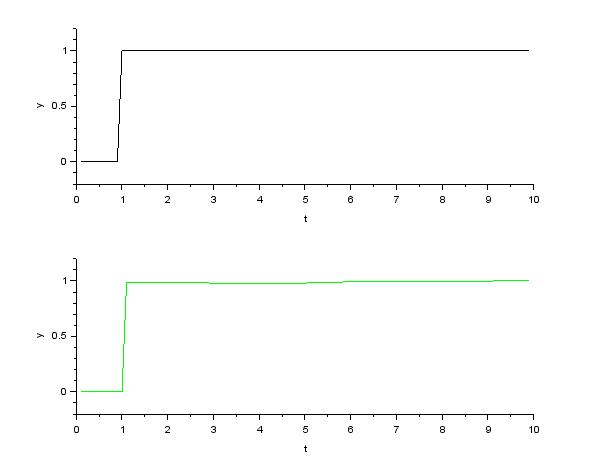
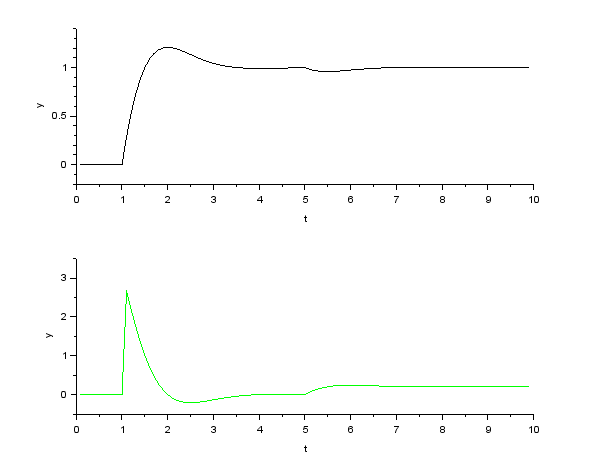
電流フィードバック制御、トルク制御(PI 制御)
| Scilab |
|---|
--> clear
--> Ra = 1; La = 0.1; J = 1; Kt = 1; Ke = Kt;
--> tau_d = -1;
--> tau_ast = 1;
--> Gdrv = 10;
--> Gc = 6; Gci = 5;
|
(Xcos のプログラムはこちら)
シミュレーション結果
| \( \tau^*,\ \tau \) | \( \omega \) |
|---|
 |
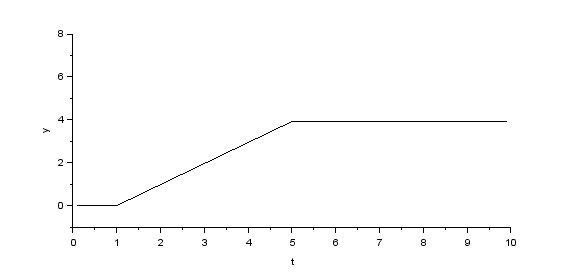 |
速度制御(PI 制御)
| Scilab |
|---|
--> clear
--> Ra = 1; La = 0.1; J = 1; Kt = 1; Ke = Kt;
--> tau_d = -0.2;
--> Gdrv = 10;
--> Gc = 6; Gci = 5;
--> Kp = 3.2; Ki = 5;
--> omega_ast = 1;
|
(Xcos のプログラムはこちら)
(Xcos で「スーパーブロック」(サブシステム)が上手く作れなかったため、階層化していない)
 |
シミュレーション結果
| \( \omega,\ \tau \) |
|---|
 |
(制御パラメタの \( K_p \)、\( K_i \) は試行錯誤で決定)
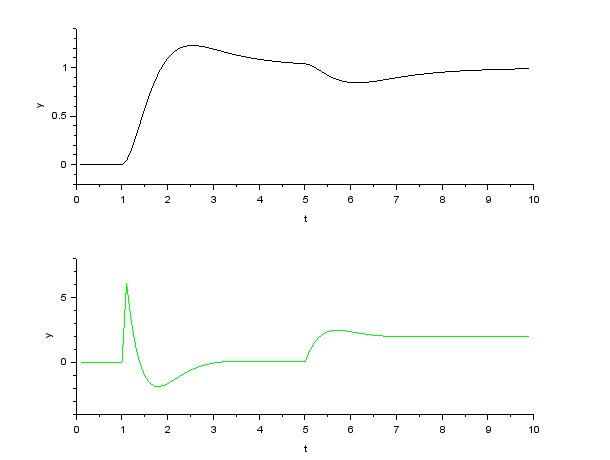
角度制御(PID 制御)
| Scilab |
|---|
--> clear
--> Ra = 1; La = 0.1; J = 1; Kt = 1; Ke = Kt;
--> tau_d = -2;
--> Gdrv = 10;
--> Gc = 6; Gci = 5;
--> Kp = 10; Ki = 5; Kd = 5;
--> theta_ast = 1;
|
(Xcos のプログラムはこちら)
(Xcos で「スーパーブロック」(サブシステム)が上手く作れなかったため、階層化していない)
 |
シミュレーション結果
| \( \theta,\ \tau \) |
|---|
 |
(制御パラメタの \( K_p \)、\( K_i \)、\( K_d \) は試行錯誤で決定)
(最終値の定理と初期値の定理)《省略》
(カスケード制御(cascade control)について)《省略》
(プロパー(proper)、厳密にプロパー(strictly proper)、インプロパー(improper)についてと近似微分)《省略》
極配置法(pole assignment method)
→ 現代制御理論
システム同定
《積み残し》
PID 制御のパラメータチューニング
(限界感度法、ステップ応答法、IMC 法(内部モデル制御(internal model control; IMC))など)《積み残し》
周波数応答
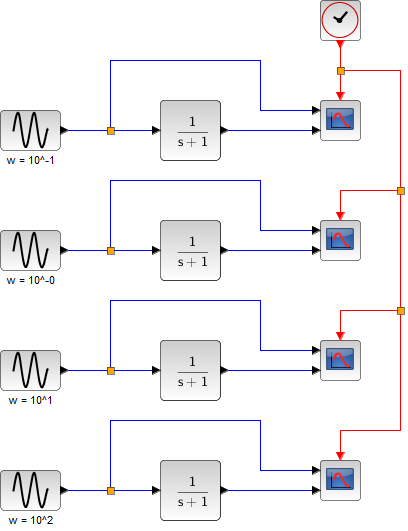
正弦波入力に対する応答の比較(伝達関数は \( \frac{1}{Ts + 1}\)(1次遅れ系)、\( T \) は \( 1 \))
Xcos によるシミュレーション
シミュレーション結果の応答波形(グラフ上段が入力波形、下段が出力波形)
| \( \omega = 10^{-1} \) | 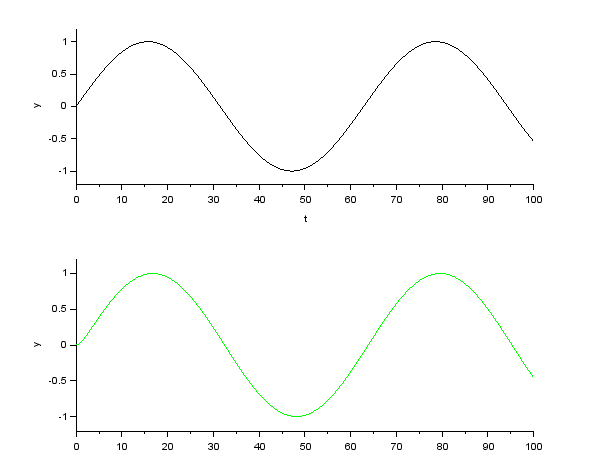 |
|---|
| \( \omega = 10^0 \) | 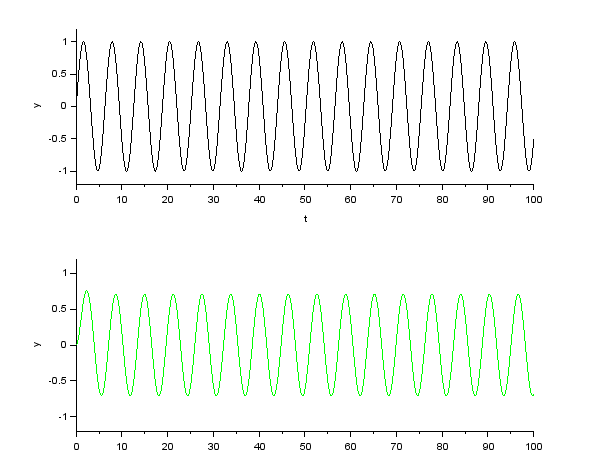 |
|---|
| \( \omega = 10^1 \) | 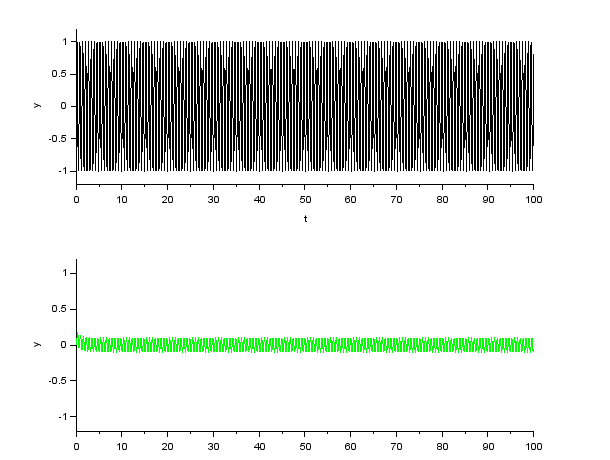 |
|---|
| \( \omega = 10^2 \) | 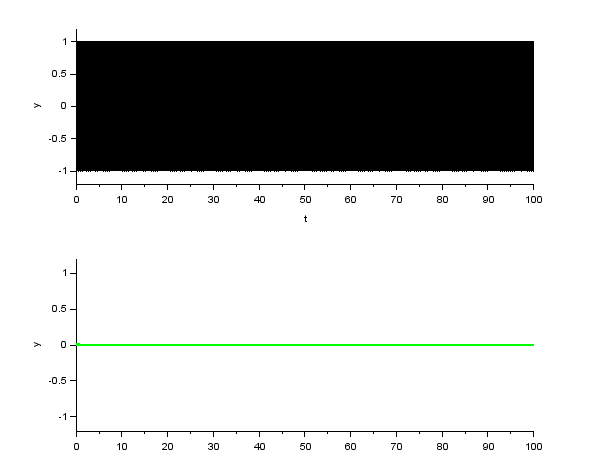 |
|---|
(Xcos のプログラムはこちら)
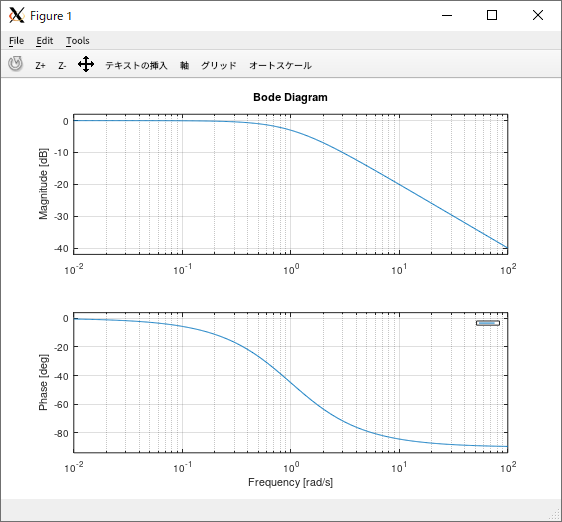
同じシステムについて Bode 線図(Bode diagram)を描画
| Octave |
|---|
octave:1> pkg load control
octave:2> bode(tf(1, [1 1]))
|
実行結果
(Bode 線図の手書きなどによる折れ線近似の方法については教科書などを参照)《省略》
デシベル(dB; decibel)(の復習)
電圧や電流などの比を表す場合には、電力 \( P \) の比と相違ないようにする
電力は\[ P = \frac{V^2}{R} = I^2 R \]であるから\[ \begin{align} 10\log_{10} \frac{P_1}{P_2} &= 10\log \frac{V_1^2/R}{V_2^2/R} = 10\log \frac{V_1^2}{V_2^2} = 10\log \left(\frac{V_1}{V_2}\right)^2 = 20\log\frac{V_1}{V_2} \\ &= 10\log\frac{I_1^2 R}{I_2^2 R} = 10\log\frac{I_1^2}{I_2^2} = 10\log\left(\frac{I_1}{I_2}\right)^2 = 20\log\frac{I_1}{I_2} \end{align} \]となる(\( V_1,\ I_1 \) は測定値、\( V_2,\ I_2 \) は基準値)
よく使われるデシベル値
対応数値表
| dB | 電圧・電流比(ゲインなど) |
|---|
| -60 | \( 0.001 \) |
| -40 | \( 0.01 \) |
| -30 | \( 1/\sqrt{10^3} \approx 0.0316 \) |
| -20 | \( 1/10 = 0.1 \) |
| -10 | \( 1/\sqrt{10} \approx 0.316 \)(約x0.3) |
| -6 | \( \approx 1/2 = 0.5 \) |
| -3 | \( \approx 1/\sqrt 2 \approx 0.7 \) |
| 0 | \( 1 \) |
| 3 | \( \approx \sqrt 2 \approx 1.4 \) |
| 6 | \( \approx 2 \) |
| 10 | \( \sqrt{10} \approx 3.16 \) (約x3) |
| 20 | \( 10 \) |
| 30 | \( \sqrt{10^3} \approx 31.6 \) |
| 40 | \( 100 \) |
| 60 | \( 1000 \) |
(正負の dB 値は「逆数」の関係)
2次遅れ系の Bode 線図と Nyquist 線図
(ナイキスト線図は、ベクトル軌跡(vector locus)とも)
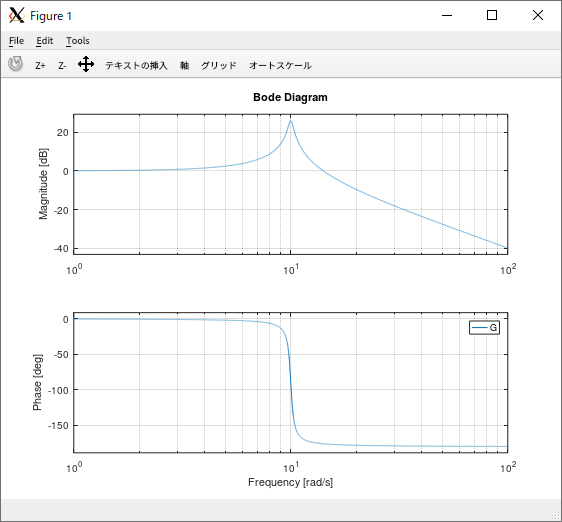
伝達関数 \( G(s) = \omega_n^2/(s^2 + 2\zeta\omega_n s + \omega_n^2) \)
| Octave |
|---|
octave:1> pkg load control
octave:2> omega_n = 10; zeta = 0.025;
octave:3> G = tf([omega_n^2], [1, 2*zeta*omega_n, omega_n^2])
Transfer function 'G' from input 'u1' to output ...
100
y1: -----------------
s^2 + 0.5 s + 100
Continuous-time model.
octave:4> figure(1); clf(1); bode(G, logspace(0, 2, 4096))
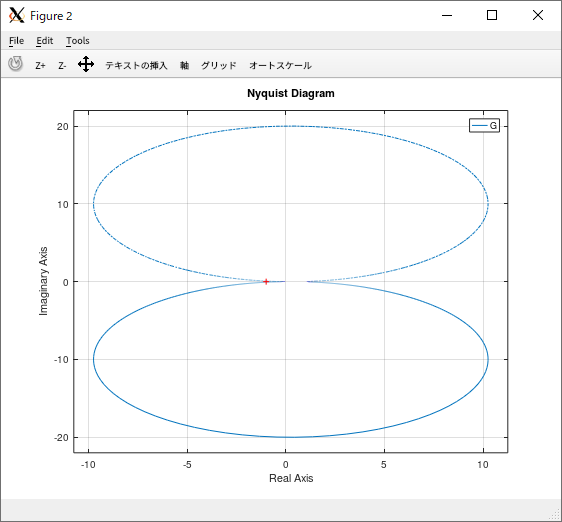
octave:5> figure(2); clf(2); nyquist(G, logspace(0, 2, 4096))
|
描画結果
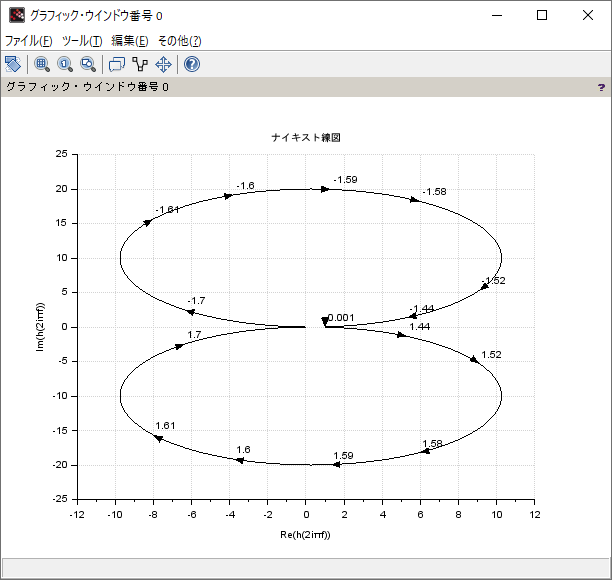
同じ伝達関数を Scilab の nyquist() 関数を使って描画
| Scilab |
|---|
--> omega_n = 10; zeta = 0.025;
--> G = syslin('c', omega_n^2/(%s^2 + 2*zeta*omega_n*(%s) + omega_n^2))
G =
100
-------------
100 +0.5s +s²
--> nyquist(G)
|
描画結果
(ゲイン余裕(gain margin)と位相余裕(phase margin)について)《省略》
(ナイキストの安定判別法)《省略》
周波数特性に基づく制御系設計
《積み残し》
教科書
© 2021 Tadakazu Nagai