- \( m \) : 質量
- \( k \) : ばね定数
- \( d \) : ダンパー係数(粘性摩擦係数)
永井 忠一 2022.7.31
質量、ばね、ダンパーからなる力学系
 |
|
運動方程式(力のつりあい)\[ \begin{align} m\ddot{x} + d\dot{x} + kx &= f \\ \ddot{x} &= -\frac{d}{m}\dot{x} - \frac{k}{m}x + \frac{1}{m}f \end{align} \]
位置(変位)と速度を選ぶ\[ \boldsymbol{x}(t) = \begin{pmatrix} x \\ \dot{x} \end{pmatrix} \](状態変数の各要素は独立であることが必要)
状態方程式\[ \frac{d}{dt}\boldsymbol{x}(t) = \begin{pmatrix} \dot{x} \\ \ddot{x} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{d}{m} \end{pmatrix}\begin{pmatrix} x \\ \dot{x} \end{pmatrix} + \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix}f \](行列微分方程式。2階の線形微分方程式が、ベクトル \( \boldsymbol{x}(t) \) に関する1階の微分方程式として書ける)
出力方程式(観測方程式とも)\[ \boldsymbol y(t) = \begin{pmatrix} 1 & 0 \end{pmatrix}\begin{pmatrix} x \\ \dot x \end{pmatrix} \](出力方程式は、代数方程式)
状態方程式と出力方程式をあわせて\[ \left\{ \begin{align} \dot{\boldsymbol x}(t) &= \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{d}{m} \end{pmatrix}\boldsymbol x(t) + \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix}f \\ \boldsymbol y(t) &= \begin{pmatrix} 1 & 0 \end{pmatrix}\boldsymbol x(t) \end{align} \right. \]状態空間表現\[ \boldsymbol u(t) \longrightarrow \boxed{\boldsymbol x(t)} \longrightarrow \boldsymbol y(t) \]入力(古典制御では操作量)\( \boldsymbol u(t) \in \mathbb R^p \)、出力(古典制御では制御量)\( \boldsymbol y(t) \in \mathbb R^q \)。そして、(システムの内部)状態 \( \boldsymbol x(t) \in \mathbb R^n \)
(cf. 古典制御(伝達関数)による表現)
n 次元の状態変数 \( \boldsymbol x \) を持つため、n 次元システムとも呼ばれる\[ \boldsymbol x(t) = \begin{bmatrix} x_1(t) \\ x_2(t) \\ \vdots \\ x_n(t) \end{bmatrix} \in \mathbb R^n,\quad \boldsymbol u(t) = \begin{bmatrix} u_1(t) \\ u_2(t) \\ \vdots \\ u_p(t) \end{bmatrix} \in \mathbb R^p,\quad \boldsymbol y(t) = \begin{bmatrix} y_1(t) \\ y_2(t) \\ \vdots \\ y_q(t) \end{bmatrix} \in \mathbb R^q \]
状態空間表現の一般形\[ \left\{ \begin{align} \dot{\boldsymbol x}(t) &= \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \\ \boldsymbol y(t) &= \mathbf C\boldsymbol x(t) + \mathbf D\boldsymbol u(t) \end{align} \right. \]システム行列 \( \mathbf A \in \mathbb R^{n\times n} \)、入力行列 \( \mathbf B \in \mathbb R^{n\times p} \)。出力行列 \( \mathbf C \in \mathbb R^{q\times n} \)、それから \( \mathbf D \in \mathbb R^{q\times p} \)
(システム \( \mathbf \Sigma \) と呼ぶこともある)システム \( (\mathbf A,\, \mathbf B,\, \mathbf C,\, \mathbf D) \)\[ \begin{bmatrix} \mathbf A \in \mathbb R^{n\times n} & \mathbf B \in \mathbb R^{n\times p} \\ \mathbf C \in \mathbb R^{q\times n} & \mathbf D \in \mathbb R^{q\times p} \end{bmatrix} \]
\( \mathbf D\boldsymbol u(t) \) は直達項。入力 \( \boldsymbol u(t) \) が、出力 \( \boldsymbol y(t) \) へダイナミクスを経由しないで現れる(機械系の例では、機構学や静力学)\[ \boldsymbol u(t) \longrightarrow \boxed{\mathbf D} \longrightarrow \boldsymbol y(t) \]\( \mathbf D = \mathbf 0 \) の場合\[ \left\{ \begin{align} \dot{\boldsymbol x}(t) &= \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \\ \boldsymbol y(t) &= \mathbf C\boldsymbol x(t) \end{align} \right. \]
状態空間表現によって表されるシステムのブロック線図
(数学)
行列指数関数指数関数 \( e^{at} \) のマクローリン展開(\( t = 0 \) まわりのテイラー展開)\[ e^{at} = 1 + \frac{1}{1!}at + \frac{2}{2!}a^2t^2 + \frac{3}{3!}a^3t^3 + \cdots = \sum_{k=0}^{\infty}\frac{1}{k!}a^kt^k \] 行列指数関数 \( e^{\mathbf At} \)\[ e^{\mathbf At} = \mathbf I + \frac{1}{1!}\mathbf At + \frac{2}{2!}\mathbf A^2t^2 + \frac{3}{3!}\mathbf A^3t^3 + \cdots = \sum_{k=0}^{\infty}\frac{1}{k!}\mathbf A^kt^k \](スカラー変数 \( a \) を n×n 行列 \( \mathbf A\) にする。\( e^{\mathbf At} \) は n×n 行列になる) 行列指数関数は以下の(指数関数としての)性質を満たす
(制御では)\( e^{\mathbf At} \) を状態遷移行列と呼ぶ(状態遷移行列 \( e^{\mathbf At} \) を掛けると、時刻 \( t_0 \) の状態 \( \boldsymbol x(t_0) \) から時刻 \( t \) の状態 \( \boldsymbol x(t) \) を求めることができる) ラプラス変換ベクトル関数や行列のラプラス変換は\[ \boldsymbol X(s) = \mathcal L\left[ \boldsymbol x(t) \right] = \begin{bmatrix} \mathcal L\left[ x_1(t) \right] \\ \mathcal L\left[ x_2(t) \right] \\ \vdots \\ \mathcal L\left[ x_n(t) \right] \end{bmatrix} = \begin{bmatrix} X_1(s) \\ X_2(s) \\ \vdots \\ X_n(s) \end{bmatrix} \]各要素をラプラス変換する(定義) (cf. スカラー関数のラプラス変換)ベクトル関数のラプラス変換の例\[ \begin{align} \mathcal L\left[ \dot{\boldsymbol x}(t) \right] = \begin{bmatrix} \mathcal L\left[ \dot x_1(t) \right] \\ \mathcal L\left[ \dot x_2(t) \right] \\ \vdots \\ \mathcal L\left[ \dot x_n(t) \right] \end{bmatrix} &= \begin{bmatrix} sX_1(s) - x_1(0) \\ sX_2(s) - x_2(0) \\ \vdots \\ sX_n(s) - x_n(0) \end{bmatrix} \\ &= \begin{bmatrix} sX_1(s) \\ sX_2(s) \\ \vdots \\ sX_n(s) \end{bmatrix} - \begin{bmatrix} x_1(0) \\ x_2(0) \\ \vdots \\ x_n(0) \end{bmatrix} \\ &= s\begin{bmatrix} X_1(s) \\ X_2(s) \\ \vdots \\ X_n(s) \end{bmatrix} - \begin{bmatrix} x_1(0) \\ x_2(0) \\ \vdots \\ x_n(0) \end{bmatrix} \\ &= s\boldsymbol X(s) - \boldsymbol x(0) \end{align} \] |
\( \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \) の解\[ \boldsymbol x(t) = e^{\mathbf A(t - t_0)}\boldsymbol x(t_0) + \int_{t_0}^{t}e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \]
確認のため、上記の式を時間 \( t \) で微分
| Maxima |
|---|
|
|
\[ {{d}\over{d\,t}}\,x\left(t\right)=B\cdot u\left(t\right)+\int_{ t_{0}}^{t}{\left(A\,e^{A\cdot \left(t-{\it \tau}\right)}\right) \cdot B\cdot u\left({\it \tau}\right)\;d{\it \tau}}+\left(A\,e^{A \cdot \left(t-t_{0}\right)}\right)\cdot x\left(t_{0}\right) \] |
Maxima の記号計算結果を、手作業で式を整理\[ \begin{align} \dot{\boldsymbol x}(t) &= \mathbf A e^{\mathbf A(t - t_0)}\boldsymbol x(t_0) + \int_{t_0}^{t}\mathbf A e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau + \mathbf B\boldsymbol u(t) \\ &= \mathbf A e^{\mathbf A(t - t_0)}\boldsymbol x(t_0) + \mathbf A\int_{t_0}^{t}e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau + \mathbf B\boldsymbol u(t) \\ &= \mathbf A\left\{ e^{\mathbf A(t - t_0)}\boldsymbol x(t_0) + \int_{t_0}^{t}e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \right\} + \mathbf B\boldsymbol u(t) \\ &= \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \end{align}\](∴ \( \boldsymbol x(t) \) が、状態方程式の解となっている)
\( t_0 = 0 \) ならば(時刻 \( t_0 \) が \( 0 \) の場合の式の形)\[ \boldsymbol x(t) = e^{\mathbf A t}\boldsymbol x_0 + \int_{0}^{t}e^{\mathbf A(t - \tau)}\mathbf B u(\tau)\, d\tau \]
(線形なので、重ね合わせの理が成り立つ。右辺第1項は自由応答(初期値応答)、第2項は外力(制御では入力)に対する応答の項。右辺第2項は、状態遷移行列と \( \mathbf B\boldsymbol u \)(入力)の畳み込み積分となる)
状態方程式の解\[ \begin{align} \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \quad \xrightarrow{\mathcal L} \quad s\boldsymbol X(s) - \boldsymbol x_0 &= \mathbf A\boldsymbol X(s) + \mathbf B\boldsymbol U(s) \\ s\boldsymbol X(s) - \mathbf A\boldsymbol X(s) &= \boldsymbol x_0 + \mathbf B\boldsymbol U(s) \\ s\mathbf I\boldsymbol X(s) - \mathbf A\boldsymbol X(s) &= \boldsymbol x_0 + \mathbf B\boldsymbol U(s) \\ (s\mathbf I - \mathbf A)\boldsymbol X(s) &= \boldsymbol x_0 + \mathbf B\boldsymbol U(s) \\ \boldsymbol x(t) = e^{\mathbf A t}\boldsymbol x_0 + \int_0^t e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \quad \xleftarrow{\mathcal L^{-1}} \quad \boldsymbol X(s) &= (s\mathbf I - \mathbf A)^{-1}\boldsymbol x_0 + (s\mathbf I - \mathbf A)^{-1}\mathbf B\boldsymbol U(s) \end{align} \]
状態方程式をラプラス変換\[ \begin{align} \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \quad \xrightarrow{\mathcal L} \quad s\boldsymbol X(s) - \boldsymbol x_0 &= \mathbf A\boldsymbol X(s) + \mathbf B\boldsymbol U(s) \\ s\boldsymbol X(s) - \mathbf A\boldsymbol X(s) &= \boldsymbol x_0 + \mathbf B\boldsymbol U(s) \\ s\mathbf I\boldsymbol X(s) - \mathbf A\boldsymbol X(s) &= \boldsymbol x_0 + \mathbf B\boldsymbol U(s) \\ \boxed{(s\mathbf I - \mathbf A)}\boldsymbol X(s) &= \boldsymbol x_0 + \mathbf B\boldsymbol U(s) \\ \boldsymbol X(s) &= \boxed{(s\mathbf I - \mathbf A)^{-1}}\boldsymbol x_0 + \boxed{(s\mathbf I - \mathbf A)^{-1}}\mathbf B\boldsymbol U(s) \end{align} \](もし、\( (s\mathbf I - \mathbf A) \) が逆行列を持つならば)\( s \) 領域で、\( \boldsymbol X(s) \) について解くことができる
時間領域の解。右辺第1項\[ \boldsymbol x(t) = \boxed{e^{\mathbf A t}\boldsymbol x_0} + \int_0^t e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \quad \xleftarrow{\mathcal L^{-1}} \quad \boldsymbol X(s) = \boxed{(s\mathbf I - \mathbf A)^{-1}\boldsymbol x_0} + (s\mathbf I - \mathbf A)^{-1}\mathbf B\boldsymbol U(s) \]の逆ラプラス変換\[ e^{\mathbf A t} = \mathcal L^{-1}\left[ (s\mathbf I - \mathbf A)^{-1} \right] \](cf. (スカラー関数の)指数関数のラプラス逆変換)
右辺第2項\[ \boldsymbol x(t) = e^{\mathbf A t}\boldsymbol x_0 + \boxed{\int_0^t e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau} \quad \xleftarrow{\mathcal L^{-1}} \quad \boldsymbol X(s) = (s\mathbf I - \mathbf A)^{-1}\boldsymbol x_0 + \boxed{(s\mathbf I - \mathbf A)^{-1}\mathbf B\boldsymbol U(s)} \]の逆ラプラス変換\[ \begin{align} \int_0^t e^{\mathbf A(t -\tau)}\mathbf B\boldsymbol u(\tau)\, d\tau &= \mathcal L^{-1}\left[ (s\mathbf I - \boldsymbol A)^{-1}\mathbf B\boldsymbol U(s) \right] \\ &= \mathcal L^{-1}\left[ \left( (s\mathbf I - \boldsymbol A)^{-1} \right) \left( \mathbf B\boldsymbol U(s) \right) \right] \\ &= \mathcal L^{-1}\left[ \mathcal L\left[ e^{\mathbf A t}\right]\mathcal L\left[ \mathbf B\boldsymbol u(t) \right] \right] \end{align} \](2つのラプラス変換を掛け合わせたものの逆ラプラス変換は、畳み込み積分)
\[ \therefore ~ \boldsymbol x(t) = e^{\mathbf A t}\boldsymbol x_0 + \int_0^t e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \]
出力方程式(観測方程式)の解(\( \boldsymbol x(t) \) に行列 \( \mathbf C \) を(左から)掛けたもの)\[ \begin{align} \boldsymbol x(t) &= e^{\mathbf A t}\boldsymbol x_0 + \int_0^t e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \\ \boldsymbol y(t) = \mathbf C\boldsymbol x(t) &= \mathbf C e^{\mathbf A t}\boldsymbol x_0 + \int_0^t \mathbf C e^{\mathbf A(t - \tau)}\mathbf B\boldsymbol u(\tau)\, d\tau \end{align} \]
(直達項がある場合には\[ \boldsymbol y(t) = \mathbf Ce^{\mathbf At}\boldsymbol x_0 + \int_0^t\mathbf Ce^{\mathbf A(t-\tau)}\mathbf B\boldsymbol u(\tau)\, d\tau + \mathbf D\boldsymbol u(t) \]となる)
無限級数展開、逆ラプラス変換により求められる(式再掲載)\[ \begin{align} e^{\mathbf{A}t} &= \mathbf{I} + \frac{1}{1!}\mathbf{A}t + \frac{1}{2!}\mathbf{A}^{2}t^2 + \frac{1}{3!}\mathbf{A}^{3}t^{3} + \cdots = \sum_{k = 0}^{\infty}\frac{1}{k!}\mathbf{A}^{k}t^{k} \\ e^{\mathbf{A}t} &= \mathcal{L}^{-1}\left[ (s\mathbf{I} - \mathbf{A})^{-1} \right] \end{align} \]
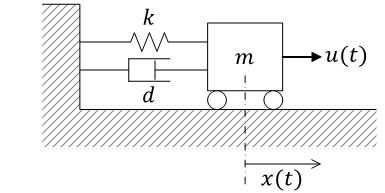
(上記システムにパラメータと初期値をあたえて時間応答を求める。)システム
 |
\[ \begin{gather} m = 1, \quad k = 5, \quad d = 6 \\ \mathbf A = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{d}{m} \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -5 & -6 \end{pmatrix}, \quad \mathbf B = \begin{pmatrix} 0 \\ \frac{1}{m} \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \end{gather}\] |
状態方程式\[ \begin{gather} \dot{\boldsymbol x}(t) = \begin{pmatrix} 0 & 1 \\ -5 & -6 \end{pmatrix}\boldsymbol x(t) + \begin{pmatrix} 0 \\ 1 \end{pmatrix}u(t) \\ \boldsymbol x(0) = \boldsymbol x_0 = \begin{pmatrix} 2 \\ 0 \end{pmatrix}, \quad u = 1, \quad t \ge 0 \end{gather} \]
状態変数\[ \boldsymbol x(t) = \begin{pmatrix} x_1 = x(t) \\ x_2 = \dot x(t) \end{pmatrix} \]
(状態変数 \( \boldsymbol x(t) \) は直接観測できるものとする。つまり、\( \boldsymbol y(t) = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\boldsymbol x(t) \))
Maxima による記号計算
| Maxima |
|---|
|
|
\[ e^{\mathbf A t}=\begin{pmatrix} {{5\,e^ {- t }}\over{4}}-{{e^ {- 5\,t }}\over{4}}&{{e^ {- t }}\over{ 4}}-{{e^ {- 5\,t }}\over{4}}\cr {{5\,e^ {- 5\,t }}\over{4}}-{{5\,e ^ {- t }}\over{4}}&{{5\,e^ {- 5\,t }}\over{4}}-{{e^ {- t }}\over{4}} \cr \end{pmatrix} \] |
|
|
\[ \boldsymbol x\left(t\right)= \begin{pmatrix} {{e^ {- 5 \,t }\,\left(4\,e^{5\,t}+45\,e^{4\,t}-9\right)}\over{20}}\cr -{{e ^ {- 5\,t }\,\left(9\,e^{4\,t}-9\right)}\over{4}}\cr \end{pmatrix} \] |
状態方程式の解のグラフ
| Maxima(つづき) |
|---|
|
|
| Octave |
|
手計算による再計算。状態遷移行列\[ e^{\mathbf At} = \mathcal L^{-1}\left[ (s\mathbf I - \mathbf A)^{-1} \right] = \begin{pmatrix} -\frac{1}{4}e^{-5t} + \frac{5}{4}e^{-t} & -\frac{1}{4}e^{-5t} + \frac{1}{4}e^{-t} \\ \frac{5}{4}e^{-5t} - \frac{5}{4}e^{-t} & \frac{5}{4}e^{-5t} - \frac{1}{4}e^{-t} \end{pmatrix} \] 状態方程式の解\[ \begin{align} \boldsymbol x(t) &= e^{\mathbf A t}\boldsymbol x_0 + \int_0^t e^{\mathbf A(t - \tau)}\mathbf B u(\tau)\, d\tau \\ &= \begin{bmatrix} -\frac{1}{4}e^{-5t} + \frac{5}{4}e^{-t} & -\frac{1}{4}e^{-5t} + \frac{1}{4}e^{-t} \\ \frac{5}{4}e^{-5t} - \frac{5}{4}e^{-t} & \frac{5}{4}e^{-5t} - \frac{1}{4}e^{-t} \end{bmatrix}\begin{pmatrix} 2 \\ 0 \end{pmatrix} + \int_0^t\begin{bmatrix} -\frac{1}{4}e^{-5(t - \tau)} + \frac{5}{4}e^{-(t - \tau)} & -\frac{1}{4}e^{-5(t - \tau)} + \frac{1}{4}e^{-(t - \tau)} \\ \frac{5}{4}e^{-5(t - \tau)} - \frac{5}{4}e^{-(t - \tau)} & \frac{5}{4}e^{-5(t - \tau)} - \frac{1}{4}e^{-(t - \tau)} \end{bmatrix}\begin{pmatrix} 0 \\ 1 \end{pmatrix}\, d\tau \\ &= \begin{bmatrix} -\frac{1}{2}e^{-5t} + \frac{5}{2}e^{-t} \\ \frac{5}{2}e^{-5t} - \frac{5}{2}e^{-t} \end{bmatrix} + \int_0^t\begin{bmatrix} -\frac{1}{4}e^{-5(t - \tau)} + \frac{1}{4}e^{-(t - \tau)} \\ \frac{5}{4}e^{-5(t - \tau)} - \frac{1}{4}e^{-(t - \tau)} \end{bmatrix}\, d\tau \\ &= \begin{bmatrix} -\frac{1}{2}e^{-5t} + \frac{5}{2}e^{-t} \\ \frac{5}{2}e^{-5t} - \frac{5}{2}e^{-t} \end{bmatrix} + \begin{bmatrix} -\frac{1}{20}e^{-5(t - t)} + \frac{1}{4}e^{-(t - t)} \\ \frac{1}{4}e^{-5(t - t)} - \frac{1}{4}e^{-(t - t)} \end{bmatrix} - \begin{bmatrix} -\frac{1}{20}e^{-5t} + \frac{1}{4}e^{-t} \\ \frac{1}{4}e^{-5t} - \frac{1}{4}e^{-t} \end{bmatrix} \\ &= \begin{bmatrix} -\frac{1}{2}e^{-5t} + \frac{5}{2}e^{-t} \\ \frac{5}{2}e^{-5t} - \frac{5}{2}e^{-t} \end{bmatrix} + \begin{bmatrix} -\frac{1}{20}e^0 + \frac{1}{4}e^0 \\ \frac{1}{4}e^0 - \frac{1}{4}e^0 \end{bmatrix} - \begin{bmatrix} -\frac{1}{20}e^{-5t} + \frac{1}{4}e^{-t} \\ \frac{1}{4}e^{-5t} - \frac{1}{4}e^{-t} \end{bmatrix} \\ &= \begin{bmatrix} -\frac{1}{2}e^{-5t} + \frac{5}{2}e^{-t} \\ \frac{5}{2}e^{-5t} - \frac{5}{2}e^{-t} \end{bmatrix} + \begin{bmatrix} -\frac{1}{20} + \frac{1}{4} \\ \frac{1}{4} - \frac{1}{4} \end{bmatrix} - \begin{bmatrix} -\frac{1}{20}e^{-5t} + \frac{1}{4}e^{-t} \\ \frac{1}{4}e^{-5t} - \frac{1}{4}e^{-t} \end{bmatrix} \\ &= \begin{bmatrix} -\frac{1}{2}e^{-5t} + \frac{5}{2}e^{-t} \\ \frac{5}{2}e^{-5t} - \frac{5}{2}e^{-t} \end{bmatrix} + \begin{bmatrix} \frac{1}{5} \\ 0 \end{bmatrix} - \begin{bmatrix} -\frac{1}{20}e^{-5t} + \frac{1}{4}e^{-t} \\ \frac{1}{4}e^{-5t} - \frac{1}{4}e^{-t} \end{bmatrix} \\ &= \begin{bmatrix} -\frac{9}{20}e^{-5t} + \frac{9}{4}e^{-t} + \frac{1}{5} \\ \frac{9}{4}e^{-5t} - \frac{9}{4}e^{-t} \end{bmatrix} \end{align} \]Maxima の答えと検算
| Maxima |
|---|
|
lsim() 関数による状態方程式の解
| Octave | |
|---|---|
| |

Octave の control パッケージのインストール(私の環境では Linux apt)
| Linux apt |
|---|
|
上記システムの状態変数\[ \boldsymbol x(t) = \begin{pmatrix} x_1(t) = x(t) \\ x_2(t) = \dot x(t) \end{pmatrix} \]の初期値 \( \boldsymbol x_0 \) を乱数で適当に決定して、状態方程式の解を可視化(相図)
 |
状態変数の初期値 \( \boldsymbol x_0 \) を変数のままとした状態方程式の解を求めて描画
| Maxima | Python |
|---|---|
|
|
|
(Maxima の fortran() 関数と、グラフ描画に Python を利用。アニメーションの作成には ImageMagick)
(定義は教科書など)
\( \mathbf A \) 行列と \( \mathbf B\) 行列を使って(\( \mathbf A \in \mathbb R^{n\times n} \)、\( \mathbf B \in \mathbb R^{n\times p} \))、可制御性行列\[ \mathbf M_\mathrm C = \begin{bmatrix} \mathbf B & \mathbf A\mathbf B & \mathbf A^2\mathbf B & \cdots & \mathbf A^{n-1}\mathbf B \end{bmatrix} \in \mathbb R^{n\times np} \]を作る。可制御性行列 \( \mathbf M_\mathrm C \) が逆行列を持つならば(正則行列(rank(\( \mathbf M_\mathrm C \)) = n (フルランク、ランク落ちしていない)、行列式 ≠ 0))、そのシステムは可制御
(証明は教科書など)
行列 \( \mathbf A \in \mathbb R^{n\times n} \) と行列 \( \mathbf C \in \mathbb R^{q\times n} \) を使って、可観測性行列\[ \mathbf M_\mathrm O = \begin{bmatrix} \mathbf C \\ \mathbf C\mathbf A \\ \mathbf C\mathbf A^2 \\ \vdots \\ \mathbf C\mathbf A^{n-1} \end{bmatrix} \in \mathbb R^{nq\times n} \]を作る。可観測性行列 \( \mathbf M_\mathrm O \) が逆行列を持つならば、そのシステムは可観測
(証明は教科書など)
システム\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \begin{pmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{d}{m} \end{pmatrix}\boldsymbol x(t) + \begin{pmatrix} 0 \\ 1 \end{pmatrix}u(t) \\ & y(t) = \begin{pmatrix} 1 & 0 \end{pmatrix}\boldsymbol x(t) \end{align} \right. \]の可制御性と可観測性の判定
| Maxima | |
|---|---|
|
|
(具体的なパラメータを与えた)システム\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \begin{pmatrix} 0 & 1 \\ -5 & -6 \end{pmatrix}\boldsymbol x(t) + \begin{pmatrix} 0 \\ 1 \end{pmatrix}u(t) \\ & y(t) = \begin{pmatrix} 1 & 0 \end{pmatrix}\boldsymbol x(t) \end{align} \right. \]の可制御性と可観測性の判定
| Octave | |
|---|---|
|
|
(Octave の control パッケージにある ctrb() 関数、obsv() 関数を使って、可制御性行列 \( \mathbf M_\mathrm C \) と可観測性行列 \( \mathbf M_\mathrm O \) を求める)
| Octave |
|---|
|
(同値変換とも)
状態空間表現\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \\ & \boldsymbol y(t) = \mathbf C\boldsymbol x(t) + \mathbf D\boldsymbol u(t) \end{align} \right. \]
正則行列 \( \mathbf T \) により、状態変数 \( \boldsymbol x(t) \) を1次変換(正則変換、座標変換)。新たな状態変数\[ \boldsymbol x(t) = \mathbf T\boldsymbol z(t) \]を定義(正則行列(逆行列を持つ)\( \boldsymbol z(t) = \mathbf T^{-1}\boldsymbol x(t) \))
状態方程式に代入して式を整理\[ \begin{align} \dot{\boldsymbol x}(t) &= \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \\ \frac{d}{dt}\left\{ \mathbf T\boldsymbol z(t) \right\} &= \mathbf A\mathbf T\boldsymbol z(t) + \mathbf B\boldsymbol u(t) \\ \mathbf T\frac{d}{dt}\boldsymbol z(t) &= \mathbf A\mathbf T\boldsymbol z(t) + \mathbf B\boldsymbol u(t) \\ \dot{\boldsymbol z}(t) &= \mathbf T^{-1}\mathbf A\mathbf T\boldsymbol z(t) + \mathbf T^{-1}\mathbf B\boldsymbol u(t) \end{align} \]
出力方程式に代入\[ \begin{align} \boldsymbol y(t) &= \mathbf C\boldsymbol x(t) + \mathbf D\boldsymbol u(t) \\ \boldsymbol y(t) &= \mathbf C\mathbf T\boldsymbol z(t) + \mathbf D\boldsymbol u(t) \end{align} \]
状態変数 \( \boldsymbol z(t) \) についての状態空間表現\[ \left\{ \begin{align} & \dot{\boldsymbol z}(t) = \boxed{\mathbf T^{-1}\mathbf A\mathbf T}\boldsymbol z(t) + \boxed{\mathbf T^{-1}\mathbf B}\boldsymbol u(t) \\ & \boldsymbol y(t) = \boxed{\mathbf C\mathbf T}\boldsymbol z(t) + \mathbf D\boldsymbol u(t) \end{align} \right. \]
得られた新たな状態空間表現\[ \left\{ \begin{align} & \dot{\boldsymbol z}(t) = \bar{\mathbf A}\boldsymbol z(t) + \bar{\mathbf B} \boldsymbol u(t) \\ & \boldsymbol y(t) = \bar{\mathbf C}\boldsymbol z(t) + \mathbf D\boldsymbol u(t) \end{align} \right. \]ここで、\[ \bar{\mathbf A} = \mathbf T^{-1}\mathbf A\mathbf T, \quad \bar{\mathbf B} = \mathbf T^{-1}\mathbf B, \quad \bar{\mathbf C} = \mathbf C\mathbf T \]
(以下、詳細は教科書など)
上記のシステムを対角正準形に変換して、可制御性と可観測性を調べる
| Maxima |
|---|
|
(\( \mathbf A \) 行列を対角化して)求めた新たな状態空間表現\[ \left\{ \begin{align} & \dot{\boldsymbol z}(t) = \begin{pmatrix} -1 & 0 \\ 0 & -5 \end{pmatrix}\boldsymbol z(t) + \begin{pmatrix} \frac{1}{4} \\ -\frac{1}{4} \end{pmatrix}u(t) \\ & y(t) = \begin{pmatrix} 1 & 1 \end{pmatrix}\boldsymbol z(t) \end{align} \right. \]より、システムは可制御で可観測
(\( \bar{\mathbf B} = \begin{pmatrix} \frac{1}{4} \\ -\frac{1}{4} \end{pmatrix} \) の要素のすべてが 0 でないため可制御。\( \bar{\mathbf C} = \begin{pmatrix} 1 & 1 \end{pmatrix} \) の要素のすべてが 0 でないため可観測)
(∵ 対角正準形で表現した場合、\( \bar{\mathbf B} \) 行列の要素に 0 があると、入力をどのように選んでも、(そのモードの)システムの状態に入力が伝わらない。また、\( \bar{\mathbf C} \) 行列の要素に 0 があると、(そのモードの)システムの状態は出力に現れない)(証明、詳細は教科書など)
システムが可制御であり、かつ、可観測であるならば、伝達関数の極と状態空間表現のシステム行列(状態方程式の \( \mathbf A \) 行列)の固有値は一致する(結論のみ)
よって、状態方程式の \( \mathbf A \) 行列の固有値の実部がすべて負ならば、システムは安定
(Maxima の eigenvalues() 関数、Octave の eig() 関数による、\( \mathbf A \) 行列の固有値の計算による)安定性判別
| Maxima | Octave |
|---|---|
|
|
∴ システムは安定
伝達関数(式を前方参照)\[ G(s) = \frac{Y(s)}{U(s)} = \mathbf c^\mathsf T(s\mathbf I - \mathbf A)^{-1}\mathbf b = \frac{\mathbf c^\mathsf T\, \mathrm{adj}(s\mathbf I - \mathbf A)\, \mathbf b}{| s\mathbf I - \mathbf A |} \](adj() は余因子行列。逆行列は、余因子行列を使って \( \boxed{ A^{-1} = \frac{1}{| A |}\mathrm{adj}(A) } \))
(伝達関数の極は、(特性方程式)\( | s\mathbf I - \mathbf A | = 0 \) の解。また、\( \mathbf c^\mathsf T\, \mathrm{adj}(s\mathbf I - \mathbf A)\, \mathbf b = 0 \) の解が零点)
(Maxima の ncharpoly() 関数、Octave の poly() 関数を使用して、Maxima の solve() 関数、Octave の roots() 関数により特性方程式の解を求める)
| Maxima | Octave |
|---|---|
|
|
(∴ システムは安定)
伝達関数から状態空間表現を求める(実現問題
(正準形
システムが可制御であれば、等価変換により、可制御正準形に変換することができる(結論のみ。詳細は教科書など)
伝達関数\[ G(s) = \frac{1}{s^2 + 6s + 5} \]状態空間表現(\(\mathbf A,\, \mathbf B,\,\mathbf C,\,\mathbf D \) 行列)
| Octave |
|---|
|
(Octave の control パッケージの tf() 関数と ss() 関数、ssdata() 関数を使用)
特性方程式は伝達関数より\[ s^2 + 6s + 5 = 0 \]
変換行列を\[ \mathbf T = \mathbf M_\mathrm C\mathbf S \]と選ぶ
(特性方程式の一般形)\[ | s\mathbf I - \mathbf A| = s^n + a_{n-1}s^{n-1} + \cdots + a_1 s+ a_0 = 0 \]ここで、行列 \( \mathbf S \) は\[ \mathbf S = \begin{bmatrix} a_1 & a_2 & a_3 & \cdots & a_{n-1} & 1 \\ a_2 & a_3 & \cdots & a_{n-1} & 1 & 0 \\ a_3 & \cdots & a_{n-1} & 1 & 0 & 0 \\ \vdots & a_{n-1} & 1 & 0 & 0 & 0 \\ a_{n-1} & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \end{bmatrix} \]と定義する(\( |\mathbf S| \ne 0 \) となり \( \mathbf S \) は正則行列)
| Maxima | Octave |
|---|---|
|
|
可制御正準形に変換された \( \bar{\mathbf A},\, \bar{\mathbf B},\, \bar{\mathbf C} \) 行列\[ \bar{\mathbf A} = \begin{bmatrix} 0 & 1 \\ -5 & -6 \end{bmatrix}, \quad \bar{\mathbf B} = \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \quad \bar{\mathbf C} = \begin{bmatrix} 1 & 0 \end{bmatrix} \](\( \bar{\mathbf A} \) の形の行列は「コンパニオン行列」と呼ばれる(また、\( \bar{\mathbf A}^\mathsf T \) の形も、同じく「コンパニオン行列」と呼ばれる))
システムが可観測であれば、等価変換により、可観測正準形に変換することができる(結論のみ。詳細は教科書など)
変換行列を\[ \mathbf T^{-1} = \mathbf S\mathbf M_\mathrm O \]と選ぶ
| Maxima | Octave |
|---|---|
|
|
(プログラム中 \( \mathbf T^{-1} \) の変数名は「Tinv」)
可観測正準形に変換された \( \bar{\mathbf A},\, \bar{\mathbf B},\, \bar{\mathbf C} \) 行列\[ \bar{\mathbf A} = \begin{bmatrix} 0 & -5 \\ 1 & -6 \end{bmatrix}, \quad \bar{\mathbf B} = \begin{bmatrix} 1 \\ 0 \end{bmatrix}, \quad \bar{\mathbf C} = \begin{bmatrix} 0 & 1 \end{bmatrix} \]
(あたえられた伝達関数 \( G(s) \) に対する実現が(状態空間表現が)可制御かつ可観測なとき、最小実現という。可制御でないとき、もしくは可観測ではないときは、システムの内部で極零相殺が起きている。最小実現とは、最も少ない状態変数の次元数で表現できているという意味)
Octave の control パッケージの minreal() 関数を用いて、既約ではない伝達関数(約分されていない伝達関数)\[ G(s) = \frac{s + 1}{s^3 + 7s^2 + 11s + 5} \]から、既約な伝達関数(約分された伝達関数)を求める
| Octave |
|---|
|
(記号計算ソフトウェアを用いて、上記の計算を確認)
| Maxima | Python SymPy |
|---|---|
|
|
(Python では、「**」はべき乗の演算子)
既約な伝達関数\[ G(s) = \frac{1}{s^{2} + 6 s + 5} \]
Python の SymPy ライブラリのインストール(私の環境では Linux apt)
| Linux apt |
|---|
|
状態空間表現から伝達関数を求める。1入力1出力システム\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \boldsymbol bu(t) \\ & y(t) = \boldsymbol c^\mathsf T\boldsymbol x(t) + du(t) \end{align} \right. \]を、初期値をすべて 0 としてラプラス変換
状態方程式\[ \begin{align} \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \boldsymbol bu(t) \quad \xrightarrow{\mathcal L} \quad s\boldsymbol X(s) &= \mathbf A\boldsymbol X(s) + \boldsymbol bU(s) \\ s\boldsymbol X(s) - \mathbf A\boldsymbol X(s) &= \boldsymbol bU(s) \\ s\mathbf I\boldsymbol X(s) - \mathbf A\boldsymbol X(s) &= \boldsymbol bU(s) \\ (s\mathbf I - \mathbf A)\boldsymbol X(s) &= \boldsymbol bU(s) \\ \boldsymbol X(s) &= (s\mathbf I - \mathbf A)^{-1}\boldsymbol bU(s) \end{align} \](\( (s\mathbf I - \mathbf A) \) が正則ならば(逆行列を持つなら)\( \boldsymbol X(s) \) について解くことができる)
出力方程式\[ y(t) = \boldsymbol c^\mathsf T\boldsymbol x(t) + du(t) \quad \xrightarrow{\mathcal L} \quad Y(s) = \boldsymbol c^\mathsf T\boldsymbol X(s) + dU(s) \](代数方程式)
式 \( \boxed{ Y(s) = \boldsymbol c^\mathsf T\boldsymbol X(s) + dU(s) } \) に \( \boxed{ \boldsymbol X(s) = (s\mathbf I - \mathbf A)^{-1}\boldsymbol bU(s) } \) を代入して式を変形\[ \begin{align} Y(s) &= \boldsymbol c^\mathsf T(s\mathbf I - \mathbf A)^{-1}\boldsymbol bU(s) + dU(s) \\ Y(s) &= \left(\boldsymbol c^\mathsf T(s\mathbf I - \mathbf A)^{-1}\boldsymbol b + d \right)U(s) \\ \frac{Y(s)}{U(s)} &= \boldsymbol c^\mathsf T(s\mathbf I - \mathbf A)^{-1}\boldsymbol b + d \end{align} \]
伝達関数の定義は、入力のラプラス変換分の出力のラプラス変換\[ G(s) = \frac{Y(s)}{U(s)} = \boldsymbol c^\mathsf T(s\mathbf I - \mathbf A)^{-1}\boldsymbol b + d \](伝達関数はスカラー)
(上記の公式にしたがって、)システム\[ \mathbf A = \begin{bmatrix} 0 & 1 \\ -5 & -6 \end{bmatrix}, \quad \boldsymbol b = \begin{bmatrix} 0 \\ 1 \end{bmatrix}, \quad \boldsymbol c^\mathsf T = \begin{bmatrix} 1 & 0 \end{bmatrix}, \quad d = 0 \]の伝達関数を求める(プログラム中 \( \boldsymbol c^\mathsf T \) の変数名は「c」)
| Maxima |
|---|
|
同じシステムの伝達関数を、Octave の control パッケージの ss() 関数と tf() 関数を用いて求める
| Octave |
|---|
|
求まった伝達関数\[ G(s) = \frac{1}{s^2 + 6 s + 5} \](伝達関数は一意に定まる)
状態変数 \( \boldsymbol x(t) \) が直接観測できるとする\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \boldsymbol b u(t) \\ & u(t) = -\boldsymbol f\boldsymbol x(t) \end{align} \right.\]ここで、\( \boldsymbol f \) は状態フィードバックゲイン(\( \boldsymbol f \) は行ベクトル)
ブロック線図
 |
閉ループ系\[ \begin{align} \dot{\boldsymbol x}(t) &= \mathbf A\boldsymbol x(t) + \boldsymbol b u(t) \\ \dot{\boldsymbol x}(t) &= \mathbf A\boldsymbol x(t) - \boldsymbol b\boldsymbol f\boldsymbol x(t) \\ \dot{\boldsymbol x}(t) &= (\mathbf A - \boldsymbol b\boldsymbol f)\boldsymbol x(t) \end{align}\]解\[ \boldsymbol x(t) = e^{(\mathbf A - \boldsymbol b\boldsymbol f)t}\boldsymbol x(0) \]
(ほかの計算方法については、教科書など)
アッカーマン
システム(システムは可制御)\[ \mathbf A = \begin{bmatrix} 0 & 1 \\ -5 & -6 \end{bmatrix}, \quad \boldsymbol b = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \] の固有値(極)が \( -7\pm 2j \) となるような状態フィードバックゲイン \( \boldsymbol f \) を求める
| Octave |
|---|
|
状態フィードバックゲイン\[ \boldsymbol f = \begin{pmatrix} 48 & 8 \end{pmatrix} \]
(検算)
| Octave(つづき) |
|---|
|
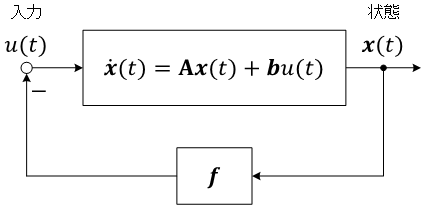
システムの時間応答を、初期値を \( \boldsymbol x_0 = \begin{pmatrix} 1 \\ 0\end{pmatrix} \) として、自由応答(\( u(t) = 0 \))と状態フィードバック制御を行った場合とで比較
| Octave | |
|---|---|
|
|
シミュレーションのためには、Octave の expm() 関数(行列指数関数)を使用して、状態遷移行列を(ラプラス変換せずに)そのまま計算。実行結果
状態変数 \( x_1 \) は位置、\( x_2 \) は速度。グラフの急峻さから、状態フィードバック制御を行ってシステムの極を \( -7\pm 2j \) へ移動するには、システムへの大きな入力が必要になることがわかる
システムの応答の速さと操作量(システムへの入力)との間にはトレードオフの関係がある(最適レギュレータ問題
2次形式
評価関数\[ J = \frac{1}{2}\int_0^\infty\left\{ \boldsymbol x^{\mathsf T}(t)\mathbf Q\boldsymbol x(t) + \boldsymbol u^{\mathsf T}(t)\mathbf R\boldsymbol u(t) \right\}\, dt \](\( J \) はスカラー)
ここで、\( \mathbf Q,\, \mathbf R \) は重み係数行列。\( \mathbf Q \) は \( n\times n \) の半正定対称行列、\( \mathbf R \) は \( p\times p \) の正定対称行列
(\( J \) を最小にする)最適制御は\[ \boldsymbol u(t) = -\mathbf F\boldsymbol x(t) = -\mathbf R^{-1}\mathbf B^{\mathsf T}\mathbf P\boldsymbol x(t) \]で与えられる。状態フィードバックゲインは\[ \begin{align} -\mathbf F\boldsymbol x(t) &= -\mathbf R^{-1}\mathbf B^{\mathsf T}\mathbf P\boldsymbol x(t) \\ \mathbf F &= \mathbf R^{-1}\mathbf B^{\mathsf T}\mathbf P \end{align} \]となる
\( \mathbf P \) は(\( \mathbf P \) 以外はすべて既知)、リカッチ代数方程式
\( \mathbf P \) は \( n\times n \) の正定対称行列になる(式の導出、解き方については、教科書など)
(正定行列、半正定行列については、線形代数)
Octave の control パッケージの lqr() 関数を使用。重みを変更しながらシミュレーション
| Octave | |
|---|---|
|
|
実行結果
| 重み \( Q_{11} = \{ 1, 10, 100, 1000 \} \) | 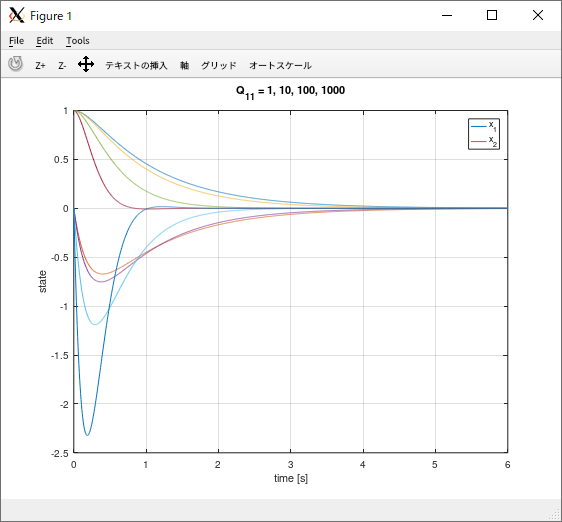 |
|---|---|
| 重み \( Q_{22} = \{ 1, 10, 100, 1000 \} \) | 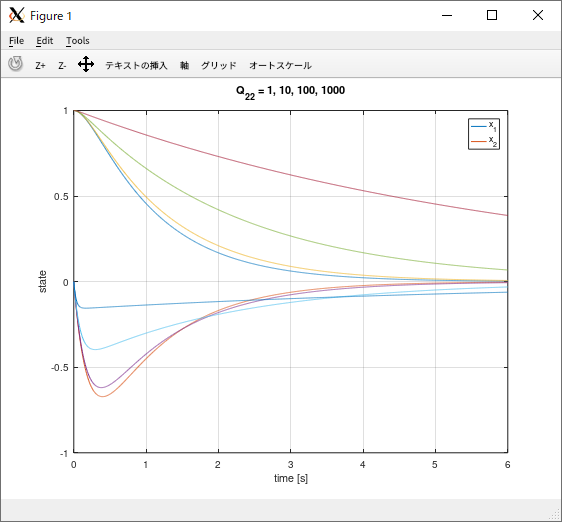 |
| 重み \( R = \{ 1, 0.1, 0.01, 0.001 \} \) | 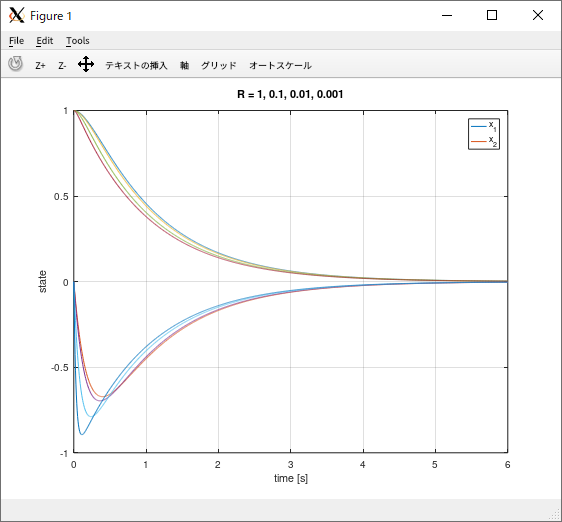 |
\( \mathbf Q \) と \( \mathbf R \) は設計者が決定して与える。通常、(対角成分がすべて正の値の)対角行列を使うことが多い
(レギュレーターでは、定常的な外乱がある場合に、状態変数が 0 にならない)
外乱を抑制し、かつ、目標値 \( r(t) \) に出力 \( y(t)\) を定常偏差
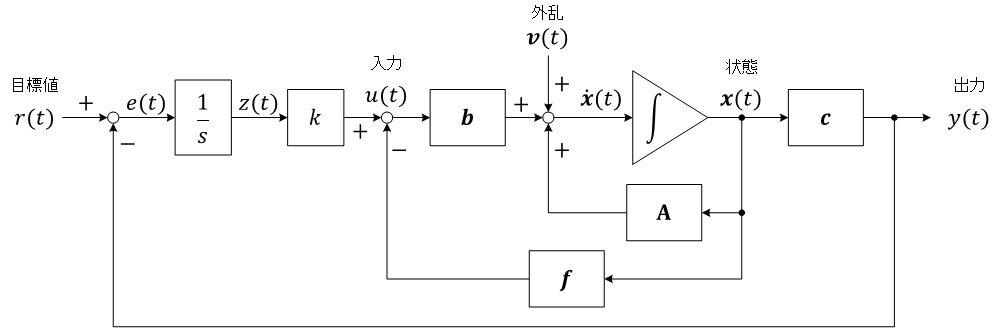
(図で、\( \boxed{ \frac{1}{s} } \) は積分器。\( \boldsymbol c \) と \( \boldsymbol f \) は行ベクトル)
(内部モデル原理
状態フィードバック制御 + 積分制御(I 制御)\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \boldsymbol b u(t) + \boldsymbol v(t) \\ & y(t) = \boldsymbol c\boldsymbol x(t) \end{align} \right. \]\[ \left\{ \begin{align} & u(t) = -\boldsymbol f\boldsymbol x(t) + k z(t) \\ & \dot z(t) = e(t) = r(t) - y(t) \end{align} \right. \]
\( \boldsymbol v(t) \) は外乱。\( k \) は積分ゲイン
状態方程式\[ \begin{bmatrix} \dot{\boldsymbol x}(t) \\ \dot z(t) \end{bmatrix} = \begin{bmatrix} \mathbf A & 0 \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} \boldsymbol b \\ 0 \end{bmatrix}u(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \]
\( \begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} \) は拡大系の状態変数
拡大系に対する、状態フィードバック制御\[ u(t) = -\begin{bmatrix} \boldsymbol f & -k \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} \]
拡大系が可制御であると仮定して、状態フィードバック制御\[ u(t) = -\begin{bmatrix} \boldsymbol f^* & -k^* \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} \]を考える。\( \boldsymbol f^* \) と \( k^* \) はシステムが漸近安定になるように適切に決定されたフィードバックゲイン
閉ループ系\[ \begin{align} \begin{bmatrix} \dot{\boldsymbol x}(t) \\ \dot z(t) \end{bmatrix} &= \begin{bmatrix} \mathbf A & 0 \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} \boldsymbol b \\ 0 \end{bmatrix}\left\{ -\begin{bmatrix} \boldsymbol f^* & -k^* \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} \right\} + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ &= \begin{bmatrix} \mathbf A & 0 \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} \boldsymbol b \\ 0 \end{bmatrix}\begin{bmatrix} -\boldsymbol f^* & k^* \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ &= \begin{bmatrix} \mathbf A & 0 \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} -\boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ 0 & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ &= \begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix} + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \end{align} \]
\( \boldsymbol v(t) \) と \( r(t) \) はステップ信号とする
システムは内部安定
t → ∞ で\[ \begin{bmatrix} \boldsymbol 0 \\ 0 \end{bmatrix} = \begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(\infty) \\ z(\infty) \end{bmatrix} + \begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \]が成り立つ
(行列 \( \begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix} \) は安定なので(そのように \( \boldsymbol f^* \) と \( k^* \) を決定している)、すべての固有値の実部は負(≠ 0)のため逆行列を持つ \( \boxed{ |\mathbf A| = \lambda_1\lambda_2\cdots\lambda_n } \))\[ \begin{align} \begin{bmatrix} \boldsymbol 0 \\ 0 \end{bmatrix} &= \begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(\infty) \\ z(\infty) \end{bmatrix} + \begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \\ -\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(\infty) \\ z(\infty) \end{bmatrix} &= \begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \\ \begin{bmatrix} \boldsymbol x(\infty) \\ z(\infty) \end{bmatrix} &= -\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}^{-1}\begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \end{align} \]
拡大系の偏差\[ \begin{align} e(\infty) &= r_0 - y(\infty) \\ &= r_0 - \bar{\boldsymbol c}\bar{\boldsymbol x}(\infty) \\ &= r_0 - \begin{bmatrix} \boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \boldsymbol x(\infty) \\ z(\infty) \end{bmatrix} \\ &= r_0 - \begin{bmatrix} \boldsymbol c & 0 \end{bmatrix}\left\{ -\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}^{-1}\begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \right\} \\ &= r_0 + \begin{bmatrix} \boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}^{-1}\begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \\ &= r_0 + \left\{ \begin{bmatrix} 0 & -1 \end{bmatrix}\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix} \right\}\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}^{-1}\begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \\ &= r_0 + \begin{bmatrix} 0 & -1 \end{bmatrix}\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix}^{-1}\begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \\ &= r_0 + \begin{bmatrix} 0 & -1 \end{bmatrix}\begin{bmatrix} \boldsymbol v_0 \\ r_0 \end{bmatrix} \\ &= r_0 -r_0 \\ &= 0 \end{align} \](式変形のテクニック \( \boxed{ \begin{bmatrix} 0 & -1 \end{bmatrix}\begin{bmatrix} \mathbf A - \boldsymbol b\boldsymbol f^* & \boldsymbol b k^* \\ -\boldsymbol c & 0 \end{bmatrix} = \begin{bmatrix} \boldsymbol c & 0 \end{bmatrix} } \))
偏差 \(e(\infty) = 0 \) となるので \( y(\infty) = r_0 \)(∴ サーボ制御を達成)
ここで\[ \begin{gather} \bar{\boldsymbol x}(t) = \begin{bmatrix} \boldsymbol x(t) \\ z(t) \end{bmatrix}, \quad \bar{\mathbf A} = \begin{bmatrix} \mathbf A & 0 \\ -\boldsymbol c & 0 \end{bmatrix}, \quad \bar{\boldsymbol b} = \begin{bmatrix} \boldsymbol b \\ 0 \end{bmatrix}, \quad \bar{\boldsymbol f} = \begin{bmatrix} \boldsymbol f & -k \end{bmatrix} \end{gather} \]と置きなおして、行列の形で再度式を整理
拡大系の状態フィードバック制御\[ \left\{ \begin{align} & \dot{\bar{\boldsymbol x}}(t) = \bar{\mathbf A}\bar{\boldsymbol x}(t) + \bar{\boldsymbol b}u(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ & u(t) = -\bar{\boldsymbol f}\bar{\boldsymbol x}(t) \end{align} \right. \]閉ループ系 \[ \dot{\bar{\boldsymbol x}}(t) = (\bar{\mathbf A} - \bar{\boldsymbol b}\bar{\boldsymbol f})\bar{\boldsymbol x}(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \]
システム\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \begin{pmatrix} 0 & 1 \\ -5 & -6 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix}u(t) + \boldsymbol v(t) \\ & y(t) = \begin{pmatrix} 1 & 0 \end{pmatrix}\boldsymbol x(t) \end{align} \right. \]
\( \boldsymbol v(t) = \boldsymbol 0 \) として、拡大系を構成\[ \begin{bmatrix} \dot x_1(t) \\ \dot x_2(t) \\ \dot z(t) \end{bmatrix} = \begin{pmatrix} 0 & 1 & 0 \\ -5 & -6 & 0 \\ -1 & 0 & 0 \end{pmatrix}\begin{bmatrix} x_1(t) \\ x_2(t) \\ z(t) \end{bmatrix} + \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}u(t) \]
変数を置きなおして\[ \begin{gather} \dot{\bar{\boldsymbol x}}(t) = \bar{\mathbf A}\bar{\boldsymbol x}(t) + \bar{\boldsymbol b}u(t) \\ \bar{\mathbf A} = \begin{pmatrix} 0 & 1 & 0 \\ -5 & -6 & 0 \\ -1 & 0 & 0 \end{pmatrix}, \quad \bar{\boldsymbol b} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \end{gather} \]
拡大系の状態フィードバック制御\[ u(t) = -\begin{pmatrix} f_1 & f_2 & -k \end{pmatrix}\bar{\boldsymbol x}(t) \]
閉ループ系の固有値(極)を -3 の3重根とする、状態フィードバックゲイン
| Octave |
|---|
|
(※acker() 関数、place() 関数については、Octave の control パッケージのドキュメントを参照)
状態フィードバックゲイン\[ \begin{gather} \bar{\boldsymbol f} = \begin{bmatrix} f_1 & f_2 & -k \end{bmatrix} = \begin{pmatrix} 22 & 3 & -27 \end{pmatrix} \\ \boldsymbol f = \begin{pmatrix} 22 & 3 \end{pmatrix}, \quad k = 27 \end{gather}\]
ステップ状の目標値 \( r(t) = \begin{cases} r_0 & (t \ge 0) \\ 0 & (t \lt 0) \end{cases} \) と外乱 \( \boldsymbol v(t) = \begin{cases} \boldsymbol v_0 & (t \ge 0) \\ 0 & (t \lt 0) \end{cases} \) (定値外乱)に対して、定常偏差が残らないことを確認
閉ループ系\[ \begin{align} \dot{\bar{\boldsymbol x}}(t) &= (\bar{\mathbf A} - \bar{\boldsymbol b}\bar{\boldsymbol f})\bar{\boldsymbol x}(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ &= \left\{ \begin{pmatrix} 0 & 1 & 0 \\ -5 & -6 & 0 \\ -1 & 0 & 0 \end{pmatrix} - \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\begin{pmatrix} 22 & 3 & -27 \end{pmatrix} \right\}\bar{\boldsymbol x}(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ &= \left\{ \begin{pmatrix} 0 & 1 & 0 \\ -5 & -6 & 0 \\ -1 & 0 & 0 \end{pmatrix} - \begin{pmatrix} 0 & 0 & 0 \\ 22 & 3 & -27 \\ 0 & 0 & 0 \end{pmatrix} \right\}\bar{\boldsymbol x}(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \\ &= \begin{pmatrix} 0 & 1 & 0 \\ -27 & -9 & 27 \\ -1 & 0 & 0 \end{pmatrix}\bar{\boldsymbol x}(t) + \begin{bmatrix} \boldsymbol v(t) \\ r(t) \end{bmatrix} \end{align} \]
(上記と同様に)\( \dot{\bar{\boldsymbol x}}(\infty) = \boldsymbol 0 \)\[ \begin{align} \dot{\bar{\boldsymbol x}}(\infty) &= \begin{pmatrix} 0 & 1 & 0 \\ -27 & -9 & 27 \\ -1 & 0 & 0 \end{pmatrix}\bar{\boldsymbol x}(\infty) + \begin{bmatrix} \boldsymbol v(\infty) \\ r(\infty) \end{bmatrix} \\ \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix} &= \begin{pmatrix} 0 & 1 & 0 \\ -27 & -9 & 27 \\ -1 & 0 & 0 \end{pmatrix}\begin{bmatrix} x_1(\infty) \\ x_2(\infty) \\ z(\infty) \end{bmatrix} + \begin{bmatrix} v_1(\infty) \\ v_2(\infty) \\ r(\infty) \end{bmatrix} \\ -\begin{pmatrix} 0 & 1 & 0 \\ -27 & -9 & 27 \\ -1 & 0 & 0 \end{pmatrix}\begin{bmatrix} x_1(\infty) \\ x_2(\infty) \\ z(\infty) \end{bmatrix} &= \begin{bmatrix} v_1(\infty) \\ v_2(\infty) \\ r(\infty) \end{bmatrix} \\ \begin{bmatrix} x_1(\infty) \\ x_2(\infty) \\ z(\infty) \end{bmatrix} &= -\begin{pmatrix} 0 & 1 & 0 \\ -27 & -9 & 27 \\ -1 & 0 & 0 \end{pmatrix}^{-1}\begin{bmatrix} v_1(\infty) \\ v_2(\infty) \\ r(\infty) \end{bmatrix} \\ \begin{bmatrix} x_1(\infty) \\ x_2(\infty) \\ z(\infty) \end{bmatrix} &= -\begin{pmatrix} 0 & 0 & -1 \\ 1 & 0 & 0 \\ \frac{1}{3} & \frac{1}{27} & -1 \end{pmatrix}\begin{bmatrix} v_1(\infty) \\ v_2(\infty) \\ r(\infty) \end{bmatrix} \\ \begin{bmatrix} x_1(\infty) \\ x_2(\infty) \\ z(\infty) \end{bmatrix} &= \begin{pmatrix} 0 & 0 & 1 \\ -1 & 0 & 0 \\ -\frac{1}{3} & -\frac{1}{27} & 1 \end{pmatrix}\begin{bmatrix} v_1(\infty) \\ v_2(\infty) \\ r(\infty) \end{bmatrix} \\ \begin{bmatrix} x_1(\infty) \\ x_2(\infty) \\ z(\infty) \end{bmatrix} &= \begin{bmatrix} r(\infty) \\ -v_1(\infty) \\ -\frac{1}{3}v_1(\infty) - \frac{1}{27}v_2(\infty) + r(\infty) \end{bmatrix} \end{align} \]
(状態変数 \( x_1 \) は位置)\[ \therefore\, x_1(\infty) = r(\infty) \]
(直接観測することのできない、)状態変数 \( \boldsymbol x(t) \) を推定する(状態観測器)
(制御対象)システム\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \mathbf B\boldsymbol u(t) \\ & \boldsymbol y(t) = \mathbf C\boldsymbol x(t) \end{align} \right. \]
システムが可観測であれば、直接観測できない状態変数 \( \boldsymbol x(t) \) を推定できる。推定された状態変数を \( \hat{\boldsymbol x}(t) \) (\( \boldsymbol x(t) \) と \( \hat{\boldsymbol x}(t) \) は、同じ次元のベクトル)
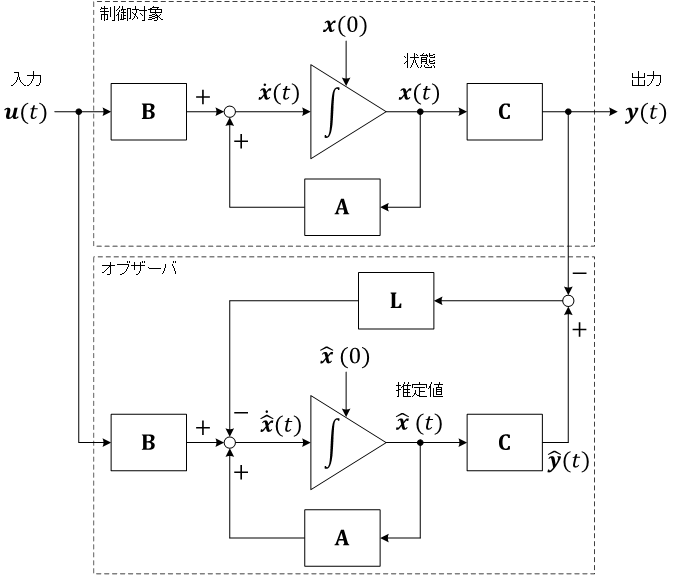
図で、\( \mathbf L \) はオブザーバゲイン。\( \boldsymbol x(0) \) と \( \hat{\boldsymbol x}(0) \) は状態変数の初期値
オブザーバ\[ \left\{ \begin{align} & \dot{\hat{\boldsymbol x}}(t) = \mathbf A\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) - \mathbf L\left( \hat{\boldsymbol y}(t) - \boldsymbol y(t) \right) \\ & \hat{\boldsymbol y}(t) = \mathbf C\hat{\boldsymbol x}(t) \end{align} \right. \]
\( \hat{\boldsymbol x}(t) \) と \( \boldsymbol x(t) \) が一致することを確認\[ \boldsymbol \eta(t) = \hat{\boldsymbol x}(t) - \boldsymbol x(t) \]と置く
(両辺を微分。オブザーバの式から制御対象のシステムの式を引く)\[ \begin{align} \boldsymbol \eta(t) &= \hat{\boldsymbol x}(t) - \boldsymbol x(t) \\ \dot{\boldsymbol \eta}(t) &= \dot{\hat{\boldsymbol x}}(t) - \dot{\boldsymbol x}(t) \\ &= \mathbf A\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) - \mathbf L\left( \hat{\boldsymbol y}(t) - \boldsymbol y(t) \right) - \mathbf A\boldsymbol x(t) - \mathbf B\boldsymbol u(t) \\ &= \mathbf A\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) - \mathbf L\left( \mathbf C\hat{\boldsymbol x}(t) - \mathbf C\boldsymbol x(t) \right) - \mathbf A\boldsymbol x(t) - \mathbf B\boldsymbol u(t) \\ &= \mathbf A\hat{\boldsymbol x}(t) - \mathbf A\boldsymbol x(t) - \mathbf L\left( \mathbf C\hat{\boldsymbol x}(t) - \mathbf C\boldsymbol x(t) \right) \\ &= \mathbf A\left( \hat{\boldsymbol x}(t) - \boldsymbol x(t) \right) - \mathbf L\mathbf C\left( \hat{\boldsymbol x}(t) - \boldsymbol x(t) \right) \\ &= \mathbf A\boldsymbol \eta(t) - \mathbf L\mathbf C\boldsymbol \eta(t) \\ &= (\mathbf A - \mathbf L\mathbf C)\boldsymbol \eta(t) \end{align} \]
推定誤差\[ \dot{\boldsymbol \eta}(t) = (\mathbf A - \mathbf L\mathbf C)\boldsymbol \eta(t) \]
(cf. 状態方程式の解)自由応答\[ \begin{gather} \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) \\ \boldsymbol x(t) = e^{\mathbf At}\boldsymbol x(0) \end{gather} \]
同様に解く\[ \boldsymbol \eta(t) = e^{(\mathbf A - \mathbf L\mathbf C)t}\boldsymbol \eta(0) \]となる
(ここで\[ \boldsymbol \eta(0) = \hat{\boldsymbol x}(0) - \boldsymbol x(0) \]で \( \boldsymbol \eta(0) \) は未知)
もし、漸近安定(行列 \( \boxed{ (\mathbf A - \mathbf L\mathbf C) } \) のすべての固有値の実部が負)ならば\[ \lim_{t \to \infty}\boldsymbol\eta(t) = \boldsymbol 0 \]となり\[ \therefore\, \hat{\boldsymbol x}(\infty) = \boldsymbol x(\infty) \]
(行列 \( \boxed{ (\mathbf A - \mathbf L\mathbf C) } \) の固有値をオブザーバの極)
システム\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \begin{pmatrix} 0 & 1 \\ -5 & -6 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix}u(t) \\ & y(t) = \begin{pmatrix} 1 & 0 \end{pmatrix}\boldsymbol x(t) \end{align} \right. \]
オブザーバの極(\( \mathbf A - \mathbf L\mathbf C \) の固有値)を \( -7,\, -8 \) に配置
(可制御性と可観測性の双対性
\( \mathbf A^\mathsf T \rightarrow \mathbf A^*,\, \mathbf C^\mathsf T \rightarrow \mathbf B^* \) と置き換え、状態フィードバック制御による極配置と同様に解く
| Octave |
|---|
|
オブザーバゲイン\[ \mathbf L = \begin{pmatrix} 9 \\ -3 \end{pmatrix} \]
(制御対象のシステムの極に対して、オブザーバの極を適切に配置する → 教科書など)
(オブザーバゲイン \( \mathbf L \) と状態フィードバックゲイン \( \mathbf F \) とは、独立に設計できる → 教科書など)
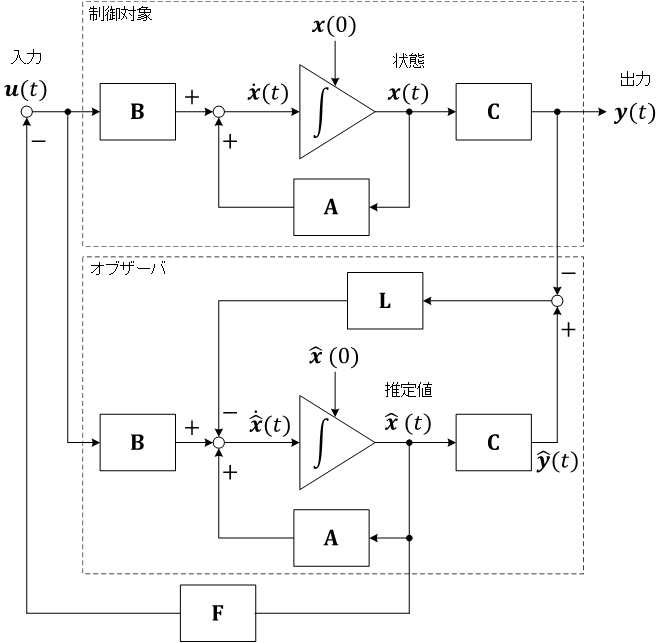
オブザーバを用いた状態フィードバック制御\[ \left\{ \begin{align} & \boldsymbol u(t) = -\mathbf F\hat{\boldsymbol x}(t) \\ & \dot{\hat{\boldsymbol x}}(t) = \left( \mathbf A - \mathbf L\mathbf C \right)\hat{\boldsymbol x}(t) + \mathbf L\boldsymbol y(t) + \mathbf B\boldsymbol u(t) \end{align} \right. \]
(オブザーバの式)\[ \boxed{ \begin{align} \dot{\hat{\boldsymbol x}}(t) &= \mathbf A\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) - \mathbf L\left( \hat{\boldsymbol y}(t) - \boldsymbol y(t) \right) \\ &= \mathbf A\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) - \mathbf L\left( \mathbf C\hat{\boldsymbol x}(t) - \boldsymbol y(t) \right) \\ &= \mathbf A\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) - \mathbf L\mathbf C\hat{\boldsymbol x}(t) + \mathbf L\boldsymbol y(t) \\ &= \left\{ \mathbf A\hat{\boldsymbol x}(t) - \mathbf L\mathbf C\hat{\boldsymbol x}(t) \right\} + \mathbf B\boldsymbol u(t) + \mathbf L\boldsymbol y(t) \\ &= \left( \mathbf A - \mathbf L\mathbf C \right)\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) + \mathbf L\boldsymbol y(t) \end{align} }\]
オブザーバと状態フィードバック制御の併合系
(制御対象の状態方程式\[ \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) - \mathbf B\mathbf F\hat{\boldsymbol x}(t) \]と、オブザーバの式\[ \boxed{ \begin{align} \dot{\hat{\boldsymbol x}}(t) &= \left( \mathbf A - \mathbf L\mathbf C \right)\hat{\boldsymbol x}(t) + \mathbf B\boldsymbol u(t) + \mathbf L\boldsymbol y(t) \\ &= \left( \mathbf A - \mathbf L\mathbf C \right)\hat{\boldsymbol x}(t) - \mathbf B\mathbf F\hat{\boldsymbol x}(t) + \mathbf L\mathbf C\boldsymbol x(t) \\ &= \left( \mathbf A - \mathbf L\mathbf C - \mathbf B\mathbf F \right)\hat{\boldsymbol x}(t) + \mathbf L\mathbf C\boldsymbol x(t) \end{align} } \]とを\[ \left\{ \begin{align} & \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) - \mathbf B\mathbf F\hat{\boldsymbol x}(t) \\ & \dot{\hat{\boldsymbol x}}(t) = \mathbf L\mathbf C\boldsymbol x(t) + \left( \mathbf A - \mathbf L\mathbf C - \mathbf B\mathbf F \right)\hat{\boldsymbol x}(t) \end{align} \right. \]行列の形で再度式を整理)\[ \begin{bmatrix} \dot{\boldsymbol x}(t) \\ \dot{\hat{\boldsymbol x}}(t) \end{bmatrix} = \begin{pmatrix} \mathbf A & -\mathbf B\mathbf F \\ \mathbf L\mathbf C & \mathbf A - \mathbf B\mathbf F - \mathbf L\mathbf C \end{pmatrix}\begin{bmatrix} \boldsymbol x(t) \\ \hat{\boldsymbol x}(t) \end{bmatrix}\]
併合系の固有値(システムの極)が、状態フィードバック制御の閉ループ系の固有値とオブザーバの固有値からなることを確認
(上記の計算結果)
固有値(閉ループシステムの極) : \( -7\pm 2j \)
| Octave |
|---|
|
併合系の設計。状態フィードバック制御の設計とオブザーバの設計とは、独立して設計することができる(詳細や証明は、教科書など)
状態フィードバックゲイン \( \mathbf F \) は、状態変数 \( \boldsymbol x(t) \) がすべて観測できるとして設計
オブザーバが推定した状態変数 \( \hat{\boldsymbol x}(t) \) を用いて状態フィードバック制御を行う
数値解法による、状態方程式の解(数値積分)
システム\[ \begin{gather} \dot{\boldsymbol x}(t) = \mathbf A\boldsymbol x(t) + \mathbf Bu(t) \\ \mathbf A = \begin{bmatrix} 0 & 1 \\ -5 & -6 \end{bmatrix},\quad \mathbf B = \begin{bmatrix} 0 \\ 1 \end{bmatrix} \end{gather} \]の時間応答
状態変数の初期値は \( \boldsymbol x_0 = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \)、入力 \( u(t) \) は矩形波(ここでは、状態変数 \( \boldsymbol x(t) \) は直接観測できるとする)
プログラム
| Octave | Python |
|---|---|
|
|
解(シミュレーション結果)
上記のシステムの解。状態変数の初期値は \( \boldsymbol x_0 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \)、入力は一定値の \( u(t) = 1 \) とする
プログラム(オイラー法)
| Octave |
|---|
|
| Python |
|
(オブザーバの状態変数の初期値は \( \hat{\boldsymbol x}_0 = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \) としている)
実行結果
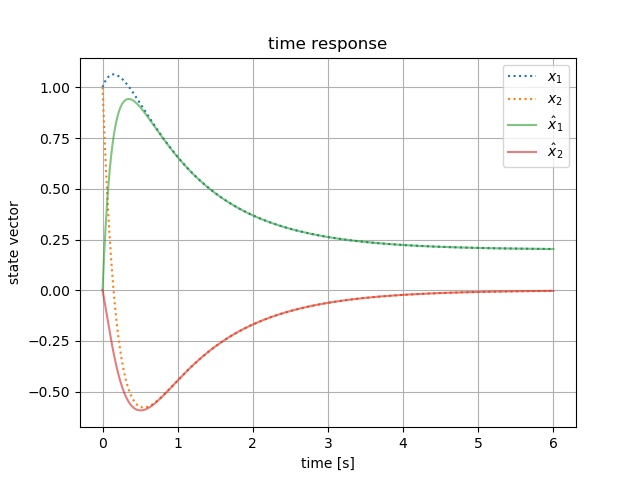
(∴ 設計したオブザーバが状態を推定できていることがわかる)
同じシステムに対して、入力 \( u(t) \) を矩形波とする
プログラム
| Octave | ||
|---|---|---|
|
|
|
シミュレーション結果
考えているシステム(系)
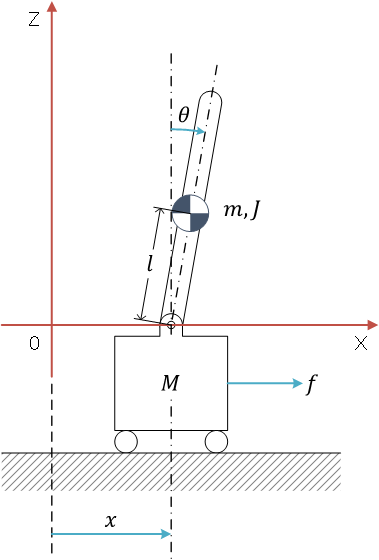 |
(振り子と台車ともに、粘性抵抗係数 \( \mu \) は考慮していない)
(振り子の関節トルク \( \tau \) は発生することができない) |
(解析力学より)ラグランジュの運動方程式\[ \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = Q - \frac{\partial F}{\partial \dot{q}} \]
F は散逸エネルギー(散逸関数)。粘性摩擦を考慮していないので(粘性摩擦係数 \( \mu = 0 \))、散逸エネルギーの項は無い\[ \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = Q \]
Q は一般化力(制御でいえば入力)。q は一般化座標(ベクトル(ベクトルで微分))
L (Lagrangian) は、運動エネルギー(の総和)からポテンシャルエネルギー(の総和)を引いたもの\[ L = T - U \]
振り子の運動エネルギー。振り子の重心の位置\[ x_g = x + l\sin(\theta),\quad z_g = l\cos(\theta) \]重心の速度(位置を微分して速度)\[ \dot{x}_g = \dot{x} + l\dot{\theta}\cos(\theta),\quad \dot{z}_g = l\dot{\theta}\sin(\theta) \]並進運動の運動エネルギー\[ \begin{align} \frac{1}{2}m v^2 &= \frac{1}{2}m\left( \sqrt{{\dot{x}_g}^2 + {\dot{z}_g}^2} \right)^2 \\ &= \frac{1}{2}m\left( {\dot{x}_g}^2 + {\dot{z}_g}^2 \right) \\ &= \frac{1}{2}m\left( \left( \dot{x} + l\dot{\theta}\cos(\theta) \right)^2 + \left( l\dot{\theta}\sin(\theta) \right)^2 \right) \\ &= \frac{1}{2}m\left(\dot{x}^2 + 2\dot{x}l\dot{\theta}\cos(\theta) + \left( l\dot{\theta}\cos(\theta) \right)^2 + \left( l\dot{\theta}\sin(\theta) \right)^2 \right) \\ &= \frac{1}{2}m\left( \dot{x}^2 + 2\dot{x}l\dot{\theta}\cos(\theta) + l^2\dot{\theta}^2\cos^2(\theta) + l^2\dot{\theta}^2\sin^2(\theta) \right) \\ &= \frac{1}{2}m\left( \dot{x}^2 + 2\dot{x}l\dot{\theta}\cos(\theta) + l^2\dot{\theta}^2\left( \cos^2(\theta) + \sin^2(\theta) \right) \right) \\ &= \frac{1}{2}m\left( \dot{x}^2 + 2\dot{x}l\dot{\theta}\cos(\theta) + l^2\dot{\theta}^2 \right) \end{align} \]振り子の回転運動の運動エネルギー\[ \frac{1}{2}J\dot{\theta}^2 \]
運動エネルギーの総和 T\[ \begin{align} T &= \frac{1}{2}M\dot{x}^2 + \frac{1}{2}m\left( \dot{x}^2 + 2\dot{x}l\dot{\theta}\cos\theta + l^2\dot{\theta}^2 \right) + \frac{1}{2}J\dot{\theta}^2 \\ &= \frac{1}{2}M\dot{x}^2 + \frac{1}{2}m\dot{x}^2 + m\dot{x}l\dot{\theta}\cos\theta + \frac{1}{2}m l^2\dot{\theta}^2 + \frac{1}{2}J\dot{\theta}^2 \\ &= \frac{1}{2}(M + m)\dot{x}^2 + m\dot{x}l\dot{\theta}\cos\theta + \frac{1}{2}(ml^2 + J)\dot{\theta}^2 \end{align} \]
ポテンシャルエネルギー U\[ U = mg z_g = mg l\cos\theta \]
ラグランジュ関数 L\[ \begin{align} L &= T - U \\ &= \left( \frac{1}{2}(M + m)\dot{x}^2 + m\dot{x}l\dot{\theta}\cos\theta + \frac{1}{2}(ml^2 + J)\dot{\theta}^2 \right) - mg l\cos\theta \end{align} \]
θ を一般化座標として\[ \frac{\partial L}{\partial\theta} = -m\dot{x}l\dot{\theta}\sin\theta + mgl\sin\theta \]\[ \begin{align} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta}} \right) &= \frac{d}{dt}\left( m\dot{x}l\cos\theta + (ml^2 + J)\dot{\theta} \right) \\ &= \frac{\partial (m\dot{x}l\cos\theta)}{\partial \dot{x}}\frac{d\dot{x}}{d t} + \frac{\partial (m\dot{x}l\cos\theta)}{\partial\theta}\frac{d\theta}{dt} + (ml^2 + J)\ddot{\theta} \\ &= m\ddot{x}l\cos\theta - m\dot{x}l\dot{\theta}\sin\theta + (ml^2 + J)\ddot{\theta} \end{align} \]\[ \begin{align} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{\theta}} \right) - \frac{\partial L}{\partial\theta} &= m\ddot{x}l\cos\theta - m\dot{x}l\dot{\theta}\sin\theta + (ml^2 + J)\ddot{\theta} + m\dot{x}l\dot{\theta}\sin\theta - mgl\sin\theta \\ &= m\ddot{x}l\cos\theta + (ml^2 + J)\ddot{\theta} - mgl\sin\theta \end{align} \]
同様に x を一般化座標として\[ \frac{\partial L}{\partial x} = 0 \]\[ \begin{align} \frac{d}{dt}\left( \frac{\partial L}{\partial \dot x} \right) &= \frac{d}{dt}\left( (M + m)\dot{x} + m l\dot{\theta}\cos\theta \right) \\ &= (M + m)\ddot{x} + \frac{\partial (m l\dot{\theta}\cos\theta)}{\partial \dot{\theta}}\frac{d \dot{\theta}}{dt} + \frac{\partial (m l\dot{\theta}\cos\theta)}{\partial \theta}\frac{d \theta}{dt} \\ &= (M + m)\ddot{x} + m l\ddot{\theta}\cos\theta - m l\dot{\theta}^2\sin\theta \end{align} \]
倒立振子の運動方程式(2本の連立微分方程式)\[ \left\{ \begin{align} & m\ddot{x}l\cos\theta + (ml^2 + J)\ddot{\theta} - mgl\sin\theta = 0 \\ & (M + m)\ddot{x} + m l\ddot{\theta}\cos\theta - m l\dot{\theta}^2\sin\theta = f \end{align} \right. \]
線形化(運動方程式の線形近似)(θ が十分に小さいとき、マクローリン展開の\[ \begin{align} \sin(\theta) &= \theta - \frac{1}{3!}\theta^3 + \frac{1}{5!}\theta^5 - \cdots \approx \theta \\ \cos(\theta) &= 1 - \frac{1}{2!}\theta^2 + \frac{1}{4!}\theta^4 - \cdots \approx 1 \end{align} \]高次の項を無視することができる)\[ \left\{ \begin{align} & m\ddot{x}l + (ml^2 + J)\ddot{\theta} - mgl\theta = 0 \\ & (M + m)\ddot{x} + m l\ddot{\theta} - m l\dot{\theta}^2\theta = f \end{align} \right. \]
さらに、(振り子の角度)\( \theta \approx 0 \) なだけではなく、その角速度 \( \dot\theta \approx 0 \) も成り立っていると仮定すると(2本目の方程式の左辺の第3項を消去できる)\[ \left\{ \begin{align} & m\ddot{x}l + (ml^2 + J)\ddot{\theta} - mgl\theta = 0 \\ & (M + m)\ddot{x} + m l\ddot{\theta} = f \end{align} \right. \]
\( \ddot x \)、\( \ddot\theta \) について連立方程式を解く
| Maxima |
|---|
|
|
\[ \left[ \left[ \ddot{x}=-{{g\,l^2\,m^2\,\theta-f\,l^2\,m-J\,f }\over{\left(M\,l^2+J\right)\,m+J\,M}} , \ddot\theta={{\left(g\,l\, m^2+M\,g\,l\,m\right)\,\theta-f\,l\,m}\over{\left(M\,l^2+J\right) \,m+J\,M}} \right] \right] \] |
もともと2階の微分方程式だったものを、1階の微分方程式として書き直す\[ \left\{ \begin{align} &\frac{d}{dt} x = \dot x \\ &\frac{d}{dt}\theta = \dot\theta \\ &\frac{d}{dt}\dot x \left( = \ddot x \right) = -{{g\,l^2\,m^2\,\theta-f\,l^2\,m-J\,f}\over{\left(M\,l^2+J\right)\,m+J\,M}} \\ &\frac{d}{dt}\dot\theta \left(= \ddot\theta \right) = {{\left(g\,l\,m^2+M\,g\,l\,m\right)\,\theta-f\,l\,m}\over{\left(M\,l^2+J\right)\,m+J\,M}} \end{align} \right. \]
(外力)f はシステムへの入力。変数 f を含む項と含まない項とに分ける\[ \left\{ \begin{align} &\frac{d}{dt} x = \dot x \\ &\frac{d}{dt}\theta = \dot\theta \\ &\frac{d}{dt}\dot x = -{{g\,l^2\,m^2\,\theta}\over{\left(M\,l^2+J\right)\,m+J\,M}} + {{l^2\,m+J}\over{\left(M\,l^2+J\right)\,m+J\,M}}\,f \\ &\frac{d}{dt}\dot\theta = {{\left(g\,l\,m^2+M\,g\,l\,m\right)\,\theta}\over{\left(M\,l^2+J\right)\,m+J\,M}} - {{l\,m}\over{\left(M\,l^2+J\right)\,m+J\,M}}\,f \end{align} \right. \]
θ は変数(振り子の姿勢)\[ \left\{ \begin{align} &\frac{d}{dt} x = \dot x \\ &\frac{d}{dt}\theta = \dot\theta \\ &\frac{d}{dt}\dot x = -{{g\,l^2\,m^2}\over{\left(M\,l^2+J\right)\,m+J\,M}}\,\theta + {{l^2\,m+J}\over{\left(M\,l^2+J\right)\,m+J\,M}}\,f \\ &\frac{d}{dt}\dot\theta = {{g\,l\,m\,\left(m+M\right)}\over{\left(M\,l^2+J\right)\,m+J\,M}}\,\theta - {{l\,m}\over{\left(M\,l^2+J\right)\,m+J\,M}}\,f \end{align} \right. \]
行列の形で連立方程式を整理して、以下の状態方程式を得る\[ \frac{d}{dt} \begin{bmatrix} x \\ \theta \\ \dot{x} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -{{g\,l^2\,m^2}\over{\left(M\,l^2+J\right)\,m+J\,M}} & 0 & 0 \\ 0 & {{g\,l\,m\,\left(m+M\right)}\over{\left(M\,l^2+J\right)\,m+J\,M}} & 0 & 0 \end{bmatrix}\begin{bmatrix} x \\ \theta \\ \dot{x} \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ {{l^2\,m+J}\over{\left(M\,l^2+J\right)\,m+J\,M}} \\ - {{l\,m}\over{\left(M\,l^2+J\right)\,m+J\,M}} \end{bmatrix}f \]
(状態ベクトルとして \( \boldsymbol{x} = \begin{bmatrix} x & \theta & \dot{x} & \dot{\theta} \end{bmatrix}^{\mathsf{T}} \) を選んでいる)
システムの出力は台車の位置 \( x(t) \) と振り子の角速度 \( \dot\theta(t) \)\[ \boldsymbol y(t) = \begin{bmatrix} 1 & 0 & 0 & 1 \end{bmatrix}\boldsymbol x(t) \]として、オブザーバを構成して状態フィードバック制御を行う(→ 併合系)
プログラム
| Octave |
|---|
|
| Python |
|
(制御とシミュレーションには Octave、結果の可視化には Python と ImageMagick を利用)
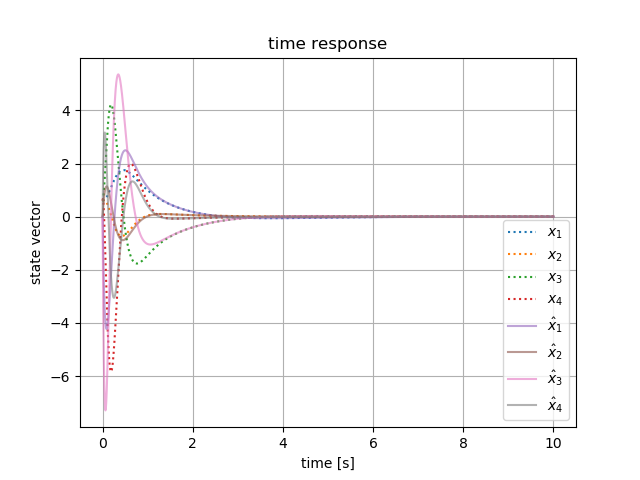 |
 |
(* シミュレーション開始直後に振り子が大きな運動をしているあたりでは、実際の現象とシミュレーションとは一致していないと考えられる(\( \theta \) と \( \dot\theta \) が十分に小さいという仮定をおいて、非線形な微分方程式を線形化しているため))
© 2022 Tadakazu Nagai