ロボット工学

永井 忠一 2018.7.28

座標変換

回転行列。Z軸まわりの回転。

MaximaOctave 
(%i1) RotateZ(angle) := matrix([cos(angle), -sin(angle), 0], [sin(angle), cos(angle), 0], [0, 0, 1]);
                                 [ cos(angle)  - sin(angle)  0 ]
                                 [                             ]
(%o1)          RotateZ(angle) := [ sin(angle)   cos(angle)   0 ]
                                 [                             ]
                                 [     0            0        1 ]
 
RotateZ = inline('[cos(angle) -sin(angle) 0; sin(angle) cos(angle) 0; 0 0 1]');

X軸まわりの回転。

(%i1) RotateX(angle) := matrix([1, 0, 0], [0, cos(angle), -sin(angle)], [0, sin(angle), cos(angle)]);
                                 [ 1      0            0       ]
                                 [                             ]
(%o1)          RotateX(angle) := [ 0  cos(angle)  - sin(angle) ]
                                 [                             ]
                                 [ 0  sin(angle)   cos(angle)  ]
 
RotateX = inline('[1 0 0; 0 cos(angle) -sin(angle); 0 sin(angle) cos(angle)]');

Y軸まわりの回転。

(%i1) RotateY(angle) := matrix([cos(angle), 0, sin(angle)], [0, 1, 0], [-sin(angle), 0, cos(angle)]);
                                 [  cos(angle)   0  sin(angle) ]
                                 [                             ]
(%o1)          RotateY(angle) := [      0        1      0      ]
                                 [                             ]
                                 [ - sin(angle)  0  cos(angle) ]
 
RotateY = inline('[cos(angle) 0 sin(angle); 0 1 0; -sin(angle) 0 cos(angle)]');

同次変換行列(homogeneous transformation matrix)

並進と回転を一つの行列で表現。

Maxima 
(%i1) R: matrix([R_11, R_12, R_13], [R_21, R_22, R_23], [R_31, R_32, R_33]);
                             [ R_11  R_12  R_13 ]
                             [                  ]
(%o1)                        [ R_21  R_22  R_23 ]
                             [                  ]
                             [ R_31  R_32  R_33 ]
(%i2) P: transpose(matrix([x, y, z]));
                                     [ x ]
                                     [   ]
(%o2)                                [ y ]
                                     [   ]
                                     [ z ]
(%i3) T: addrow(addcol(R, P), [0, 0, 0, 1]);
                            [ R_11  R_12  R_13  x ]
                            [                     ]
                            [ R_21  R_22  R_23  y ]
(%o3)                       [                     ]
                            [ R_31  R_32  R_33  z ]
                            [                     ]
                            [  0     0     0    1 ]
MathML
( R 11 R 12 R 13 x R 21 R 22 R 23 y R 31 R 32 R 33 z 0 0 0 1 ) matrix( [R_11, R_12, R_13, x], [R_21, R_22, R_23, y], [R_31, R_32, R_33, z], [0, 0, 0, 1] )

同次変換行列の並進と回転の順序。回転行列に左側から並進の行列を掛けている。

\( \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} R_{11} & R_{12} & R_{13} & 0 \\ R_{21} & R_{22} & R_{23} & 0 \\ R_{31} & R_{32} & R_{33} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}=\begin{bmatrix} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \) 
(%i1) R: addrow(addcol(matrix([R_11, R_12, R_13], [R_21, R_22, R_23], [R_31, R_32, R_33]), [0, 0, 0]), [0, 0, 0, 1]);
                            [ R_11  R_12  R_13  0 ]
                            [                     ]
                            [ R_21  R_22  R_23  0 ]
(%o1)                       [                     ]
                            [ R_31  R_32  R_33  0 ]
                            [                     ]
                            [  0     0     0    1 ]
(%i2) P: addrow(addcol(ident(3), [x, y, z]), [0, 0, 0, 1]);
                                [ 1  0  0  x ]
                                [            ]
                                [ 0  1  0  y ]
(%o2)                           [            ]
                                [ 0  0  1  z ]
                                [            ]
                                [ 0  0  0  1 ]
(%i3) T: P . R;
                            [ R_11  R_12  R_13  x ]
                            [                     ]
                            [ R_21  R_22  R_23  y ]
(%o3)                       [                     ]
                            [ R_31  R_32  R_33  z ]
                            [                     ]
                            [  0     0     0    1 ]

同次変換行列の逆行列。\( (^{A}T_B)^{-1} = {^{B}T_A} \) となる。ATBは座標系Bから座標系Aへの座標変換。（プログラム中の変数名はT_AB, T_BA）

回転行列の逆行列は \( (^{A}R_B)^{-1} = (^{A}R_B)^T \) である。（プログラム中 ARBはR_AB）

\( (^{A}T_B)^{-1}=\left[ \begin{array}{c|c} {^AR_B}^T & {-{^AR_B}^T}{^At_B} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right] \) 
(%i1) R_AB: matrix([R_11, R_12, R_13], [R_21, R_22, R_23], [R_31, R_32, R_33]);
                             [ R_11  R_12  R_13 ]
                             [                  ]
(%o1)                        [ R_21  R_22  R_23 ]
                             [                  ]
                             [ R_31  R_32  R_33 ]
(%i2) P_AB: transpose(matrix([x, y, z]));
                                     [ x ]
                                     [   ]
(%o2)                                [ y ]
                                     [   ]
                                     [ z ]
(%i3) T_AB: addrow(addcol(R_AB, P_AB), [0, 0, 0, 1]);
                            [ R_11  R_12  R_13  x ]
                            [                     ]
                            [ R_21  R_22  R_23  y ]
(%o3)                       [                     ]
                            [ R_31  R_32  R_33  z ]
                            [                     ]
                            [  0     0     0    1 ]
(%i4) R_BA: transpose(R_AB);
                             [ R_11  R_21  R_31 ]
                             [                  ]
(%o4)                        [ R_12  R_22  R_32 ]
                             [                  ]
                             [ R_13  R_23  R_33 ]
(%i5) P_BA: -transpose(R_AB) . P_AB;
                       [ (- z R_31) - y R_21 - x R_11 ]
                       [                              ]
(%o5)                  [ (- z R_32) - y R_22 - x R_12 ]
                       [                              ]
                       [ (- z R_33) - y R_23 - x R_13 ]
(%i6) T_BA: addrow(addcol(R_BA, P_BA), [0, 0, 0, 1]);
              [ R_11  R_21  R_31  (- z R_31) - y R_21 - x R_11 ]
              [                                                ]
              [ R_12  R_22  R_32  (- z R_32) - y R_22 - x R_12 ]
(%o6)         [                                                ]
              [ R_13  R_23  R_33  (- z R_33) - y R_23 - x R_13 ]
              [                                                ]
              [  0     0     0                 1               ]

\( ^AT_B(^AT_B)^{-1}={^AT_B}{^BT_A}=I_4 \) ← 4x4単位行列になる\[ \begin{align} \left[ \begin{array}{c|c} ^AR_B & ^At_B \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right]\left[ \begin{array}{c|c} {^AR_B}^T & {-(^AR_B)^T}{^At_B} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right]&=\left[ \begin{array}{c|c} ^AR_B(^AR_B)^T+{^At_B}\begin{bmatrix} 0 & 0 & 0 \end{bmatrix} & -{^AR_B}{(^AR_B)^T}{^At_B}+{^At_B} \\ \hline \begin{bmatrix} 0 & 0 & 0 \end{bmatrix}{^AR_B}+1\begin{bmatrix} 0 & 0 & 0 \end{bmatrix} & -\begin{bmatrix} 0 & 0 & 0 \end{bmatrix}{(^AR_B)^T}{^At_B}+1 \end{array} \right] \\ &=\left[ \begin{array}{c|c} ^AR_B(^AR_B)^T & -{^AR_B}{(^AR_B)^T}{^At_B}+{^At_B} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right] \\ &=\left[ \begin{array}{c|c} I_3 & -I_3{^At_B}+{^At_B} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right] \\ &=\left[ \begin{array}{c|c} I_3 & -{^At_B}+{^At_B} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right] \\ &=\left[ \begin{array}{c|c} I_3 & \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \\ \hline \begin{array}{ccc} 0 & 0 & 0 \end{array} & 1 \end{array} \right]=I_4 \end{align} \]

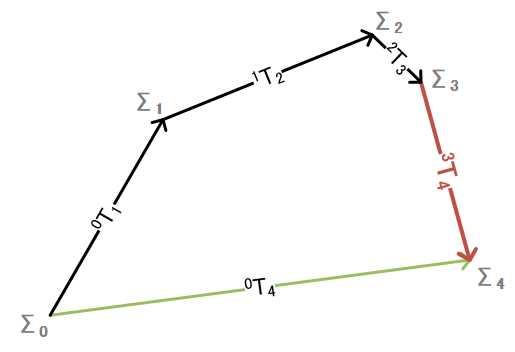
同次変換行列のチェーンルール\[ ^0T_N={^0T_1}{^1T_2}{^2T_3}\cdots{^{N-1}T_N} \]

運動学方程式

座標系 Σ0, Σ1, Σ2, Σ3, Σ4

3T4の表現\[ \begin{align} {^0T_1}{^1T_2}{^2T_3}{^3T_4}&={^0T_4} \\ {^0T_3}{^3T_4}&={^0T_4} \\ {^3T_4}&=\left((^0T_3)^{-1}\right){^0T_4} \end{align} \]

任意軸での回転（Rodrigueの回転公式）

ロドリゲスの回転公式\[ e^{a\times\theta}=I_3+a\times\sin\theta+\left(a\times\right)^2(1-\cos\theta) \]aは単位ベクトルで回転軸を表す。θは回転角度を表す。×は外積を表す

外積の計算の関係式\[ \omega\times p=\begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix}\times\begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix}=\begin{bmatrix} \omega_y p_z-\omega_z p_y \\ \omega_z p_x-\omega_x p_z \\ \omega_x p_y-\omega_y p_x \end{bmatrix}=\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix}\begin{bmatrix} p_x \\ p_y \\ p_z \end{bmatrix} \]

この行列 \( \omega\times=\begin{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \end{bmatrix} \) を歪対称行列(skew symmetric matrix)と呼ぶ

expmは行列の指数関数(普通のexp関数とは違うので注意)\[ {\rm expm}(a\times\theta)={\rm eye}(3)+a\times\sin\theta+\left(a\times\right)^2(1-\cos\theta) \]\[ {\rm expm}\begin{bmatrix} 0 & -a_z\theta & a_y\theta \\ a_z\theta & 0 & -a_x\theta \\ -a_y\theta & a_x\theta & 0 \end{bmatrix}=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}+\begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix}\sin\theta+\left(\begin{bmatrix} 0 & -a_z & a_y \\ a_z & 0 & -a_x \\ -a_y & a_x & 0 \end{bmatrix}\right)^2(1-\cos\theta) \]右辺はe（指数関数）を使わない形式（expm関数が用意されていない場合には右辺の式を使う）

回転軸を \( a=\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}\quad a=\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\quad a=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \) として計算してみる（記号計算）

Maxima
(%i1) ax: matrix([0, 0, 0], [0, 0, -1], [0, 1, 0]);
                                 [ 0  0   0  ]
                                 [           ]
(%o1)                            [ 0  0  - 1 ]
                                 [           ]
                                 [ 0  1   0  ]
(%i2) ident(3) + ax*sin(theta) + ax^^2*(1-cos(theta));
                        [ 1      0            0       ]
                        [                             ]
(%o2)                   [ 0  cos(theta)  - sin(theta) ]
                        [                             ]
                        [ 0  sin(theta)   cos(theta)  ]
 
(%i3) ax: matrix([0, 0, 1], [0, 0, 0], [-1, 0, 0]);
                                 [  0   0  1 ]
                                 [           ]
(%o3)                            [  0   0  0 ]
                                 [           ]
                                 [ - 1  0  0 ]
(%i4) ident(3) + ax*sin(theta) + ax^^2*(1-cos(theta));
                        [  cos(theta)   0  sin(theta) ]
                        [                             ]
(%o4)                   [      0        1      0      ]
                        [                             ]
                        [ - sin(theta)  0  cos(theta) ]
 
(%i5) ax: matrix([0, -1, 0], [1, 0, 0], [0, 0, 0]);
                                 [ 0  - 1  0 ]
                                 [           ]
(%o5)                            [ 1   0   0 ]
                                 [           ]
                                 [ 0   0   0 ]
(%i6) ident(3) + ax*sin(theta) + ax^^2*(1-cos(theta));
                        [ cos(theta)  - sin(theta)  0 ]
                        [                             ]
(%o6)                   [ sin(theta)   cos(theta)   0 ]
                        [                             ]
                        [     0            0        1 ]

（Maximaで行列のべき乗には「^^」演算子を使う）

MATLAB Symbolic Math Toolbox
>> ax = [0 0 0; 0 0 -1; 0 1 0]

ax =

     0     0     0
     0     0    -1
     0     1     0

>> syms theta; simplify(expm(ax*theta))

ans =

[ 1,          0,           0]
[ 0, cos(theta), -sin(theta)]
[ 0, sin(theta),  cos(theta)]
 
>> ax = [0 0 1; 0 0 0; -1 0 0]

ax =

     0     0     1
     0     0     0
    -1     0     0

>> syms theta; simplify(expm(ax*theta))

ans =

[  cos(theta), 0, sin(theta)]
[           0, 1,          0]
[ -sin(theta), 0, cos(theta)]
 
>> ax = [0 -1 0; 1 0 0; 0 0 0]

ax =

     0    -1     0
     1     0     0
     0     0     0

>> syms theta; simplify(expm(ax*theta))

ans =

[ cos(theta), -sin(theta), 0]
[ sin(theta),  cos(theta), 0]
[          0,           0, 1]

それぞれ、X軸まわりの回転行列、Y軸まわりの回転行列、Z軸まわりの回転行列になっている。

Z軸まわりにπ/3（６０度）回転（数値計算で確認）

Octave
octave:1> ax = [0 -1 0; 1 0 0; 0 0 0]
ax =

   0  -1   0
   1   0   0
   0   0   0

octave:2> theta = pi/3;
octave:3> expm(ax*theta)
ans =

   0.50000  -0.86603   0.00000
   0.86603   0.50000   0.00000
   0.00000   0.00000   1.00000
 
octave:4> eye(3) + ax*sin(theta) + ax**2*(1-cos(theta))
ans =

   0.50000  -0.86603   0.00000
   0.86603   0.50000   0.00000
   0.00000   0.00000   1.00000
 
octave:5> [cos(theta) -sin(theta) 0; sin(theta) cos(theta) 0; 0 0 1]
ans =

   0.50000  -0.86603   0.00000
   0.86603   0.50000   0.00000
   0.00000   0.00000   1.00000

回転行列に一致している（expm関数については「octave:1> help expm」などを参照）

クォータニオン(Quaternion)

四元数による回転

運動学

逆運動学(inverse kinematics)を幾何学で解く場合、ピタゴラスの定理、余弦定理、\( \sin(\theta)^2 + \cos(\theta)^2 = 1 \) や \( \tan(\theta) = \sin(\theta) / \cos(\theta) \) などの三角関数の知識を使う。

アークタンジェントの計算にはatan2()関数を使う。atan2()については「octave:1> help atan2」や「$ man 3 atan2」などを参照。

プログラムはOctave。可視化にはuicontrol()関数とグラフィックスオブジェクトハンドルを利用。（ソースコード）

３次元空間内の４自由度ロボットの順運動学と逆運動学。関節変数θ1, θ2, θ3, θ4と手先位置・姿勢x, y, z, αの関係を扱う。逆運動学は幾何学的に解いている。

アームの「くの字」の部分には複数解(multiple solutions)の問題がある。（エルボーダウンか、エルボーアップか。）ここでは適当な評価関数（前の姿勢からの関節変位のSAD）を使って動きが自然になる方を選んでいる。

解が無い（＝アームが届かない）場合や、（この関節構造の場合）解が無限にある（＝原点）という問題があるが、if文で対応している。

ヤコビ行列

順運動学の式を次のように表す。\[ p = f(q) \]

一般の場合を考える。pは手先位置・姿勢。qは関節変数。\[ p = \left( \begin{array}{c} p_{1} \\ p_{2} \\ \vdots \\ p_{n} \end{array} \right), q = \left( \begin{array}{c} q_{1} \\ q_{2} \\ \vdots \\ q_{m} \end{array} \right) \]

冗長な関節構造をとらない場合を考える。たとえば \(n = m = 6\) の通常のロボット。

順運動学の式の両辺を時間で微分すると、速度の関係式が得られる。\[ \dot{p} = \frac{\partial f(q)}{\partial q}\dot{q} \]

偏微分のところがヤコビ行列(Jacobian)である。記号はJを使う。\[ J(q) = \frac{\partial f(q)}{\partial q} = \left( \begin{array}{ccc} \frac{\partial f_{1}(q)}{\partial q_{1}} & \ldots & \frac{\partial f_{1}(q)}{\partial q_{6}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{6}(q)}{\partial q_{1}} & \ldots & \frac{\partial f_{6}(q)}{\partial q_{6}} \end{array} \right) \]

Jは定数行列ではなくqの関数である。qは関節変数なので、ロボットの姿勢によりJ(q)が定まる。J(q)の情報を使うことによって、ロボットの状態を推察することができる。

J(q)を考えるとき、微少時間で成り立つ関係を考えることに相当する。これが、順運動学方程式を時間で微分することの意味である。\[ \dot{p} = J(q)\dot{q} \]\[ \dot{q} = J^{-1}(q)\dot{p} \]

n = m の場合 J(q) は正方行列になる。det J(q) = 0 のとき J-1(q) は存在しない。（行列式が0のとき逆行列は計算できない。）この場合を特異姿勢という。

3DOFマニピュレータのヤコビ行列

3DOF平面マニピュレータ\[ p=f(q),\quad p=\begin{bmatrix} x \\ y \\ \phi \end{bmatrix},\quad q=\begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \end{bmatrix} \]

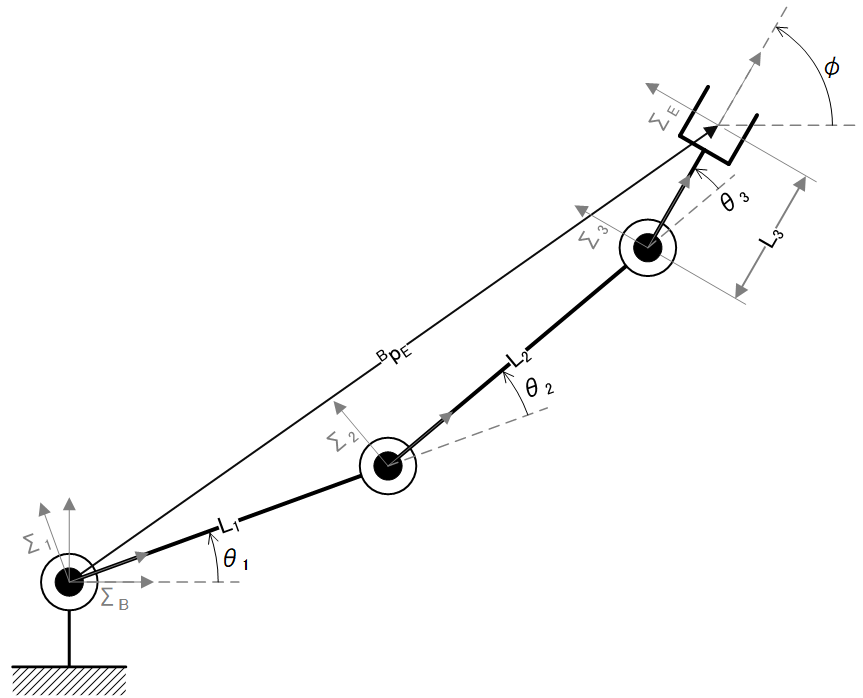
順運動学(F.K.)\[ \begin{align} x &= L_1\cos(\theta_1)+L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) \\ y &= L_1\sin(\theta_1)+L_2\sin(\theta_1+\theta_2)+L_3\sin(\theta_1+\theta_2+\theta_3) \\ \phi &= \theta_1+\theta_2+\theta_3 \end{align} \]

ヤコビ行列\[ J=\begin{bmatrix} \frac{\partial fx}{\partial \theta_1} & \frac{\partial fx}{\partial \theta_2} & \frac{\partial fx}{\partial \theta_3} \\ \frac{\partial fy}{\partial \theta_1} & \frac{\partial fy}{\partial \theta_2} & \frac{\partial fy}{\partial \theta_3} \\ \frac{\partial f\phi}{\partial \theta_1} & \frac{\partial f\phi}{\partial \theta_2} & \frac{\partial f\phi}{\partial \theta_3} \end{bmatrix}=\begin{bmatrix} -L_1\sin(\theta_1)-L_2\sin(\theta_1+\theta_2)-L_3\sin(\theta_1+\theta_2+\theta_3) & -L_2\sin(\theta_1+\theta_2)-L_3\sin(\theta_1+\theta_2+\theta_3) & -L_3\sin(\theta_1+\theta_2+\theta_3) \\ L_1\cos(\theta_1)+L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) & L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) & L_3\cos(\theta_1+\theta_2+\theta_3) \\ 1 & 1 & 1 \end{bmatrix} \]

速度の関係式\[ \dot{p}=J(q)\dot{q} \]

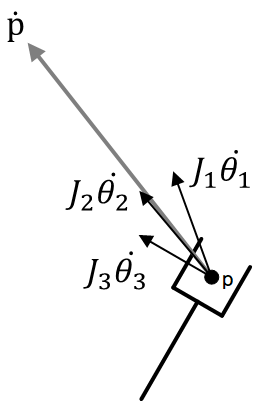
（ヤコビ行列に対してJ1, J2, J3の列ベクトルを定義する）\[ J=\begin{bmatrix} J_1 & J_2 & J_3 \end{bmatrix} \\ \dot p=J_1\dot{\theta_1}+J_2\dot{\theta_2}+J_3\dot{\theta_3} \\ \begin{bmatrix} \dot x \\ \dot y \\ \dot\phi \end{bmatrix}=\begin{bmatrix} -L_1\sin(\theta_1)-L_2\sin(\theta_1+\theta_2)-L_3\sin(\theta_1+\theta_2+\theta_3) \\ L_1\cos(\theta_1)+L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) \\ 1 \end{bmatrix}\dot{\theta_1}+\begin{bmatrix} -L_2\sin(\theta_1+\theta_2)-L_3\sin(\theta_1+\theta_2+\theta_3) \\ L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) \\ 1 \end{bmatrix}\dot{\theta_2}+\begin{bmatrix} -L_3\sin(\theta_1+\theta_2+\theta_3) \\ L_3\cos(\theta_1+\theta_2+\theta_3) \\ 1 \end{bmatrix}\dot{\theta_3} \]

Jの物理的な意味。手先速度\( \begin{bmatrix} \dot x \\ \dot y \end{bmatrix} \)

角速度\( \dot\phi \)

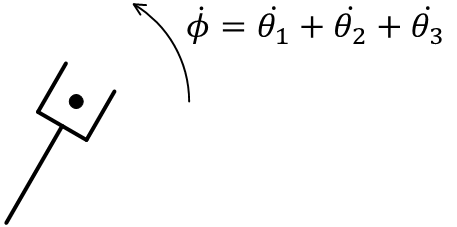
加速度の関係式\[ \ddot p=J(q)\ddot q+\dot J(q)\dot q \]（\( \dot J \)はJの各要素を時間で微分する）

静力学

力が釣り合っている状態での関節トルクτと手先力Fの問題を扱う。

仮想仕事の原理によるつり合いの式と上記の速度の関係式を連立して解くと、手先力Fと関節トルクτの関係が得られる。（式の導出は教科書などを参照。）

静力学関係式(equation of statics)。手先力Fから関節トルクτを求める。\[ \tau = J^{T}(q)F \]

関節トルクからτ手先力Fを求める。\[ F = \left(J^{T}\left(q\right)\right)^{-1}\tau \]

ただし、逆行列が求まるときのみ。特異姿勢の場合にはτからFは求められない。

3DOFマニピュレータの静力学

上記の3DOFマニピュレータがθ1=0, θ2=π/2[rad], θ3=π/2[rad]の姿勢をとるとき、FA, FB, FCの手先力を発生するために必要な関節駆動力τ1, τ2, τ3をそれぞれ求める。ただし、Nはモーメントを表す

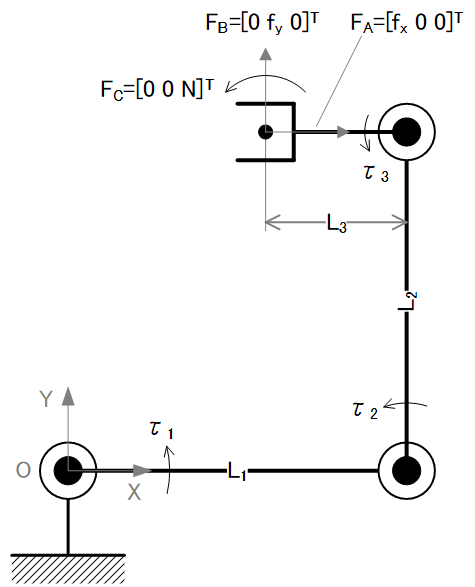
静力学\[ \tau=J^TF,\quad J^T=\begin{bmatrix} -L_1\sin(\theta_1)-L_2\sin(\theta_1+\theta_2)-L_3\sin(\theta_1+\theta_2+\theta_3) & L_1\cos(\theta_1)+L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) & 1 \\ -L_2\sin(\theta_1+\theta_2)-L_3\sin(\theta_1+\theta_2+\theta_3) & L_2\cos(\theta_1+\theta_2)+L_3\cos(\theta_1+\theta_2+\theta_3) & 1 \\ -L_3\sin(\theta_1+\theta_2+\theta_3) & L_3\cos(\theta_1+\theta_2+\theta_3) & 1 \end{bmatrix}\]

関節変数\( \theta=\begin{bmatrix} \theta_1 \\ \theta_2 \\ \theta_3 \end{bmatrix}=\begin{bmatrix} 0 \\ \pi/2 \\ \pi/2 \end{bmatrix} \)（＝ロボットの姿勢）をJTに代入する\[ J^T(\theta)=\begin{bmatrix} -L_2 & L_1-L_3 & 1 \\ -L_2 & -L_3 & 1 \\ 0 & -L_3 & 1 \end{bmatrix} \]

それぞれ\[ \begin{bmatrix} J^T(\theta) \end{bmatrix}\begin{bmatrix} f_x \\ 0 \\ 0 \end{bmatrix}=\begin{bmatrix} -L_2f_x \\ -L_2f_x \\ 0 \end{bmatrix},\quad \begin{bmatrix} J^T(\theta) \end{bmatrix}\begin{bmatrix} 0 \\ f_y \\ 0 \end{bmatrix}=\begin{bmatrix} (L_1-L_3)f_y \\ -L_3 f_y \\ -L_3 f_y \end{bmatrix},\quad \begin{bmatrix} J^T(\theta) \end{bmatrix}\begin{bmatrix} 0 \\ 0 \\ N \end{bmatrix}=\begin{bmatrix} N \\ N \\ N \end{bmatrix} \]となる

平面２自由度ロボットの静力学プログラム

アーム先端の赤いベクトルで手先力を表現。関節トルクは画面左下(Tau1, Tau2)で数値表示。

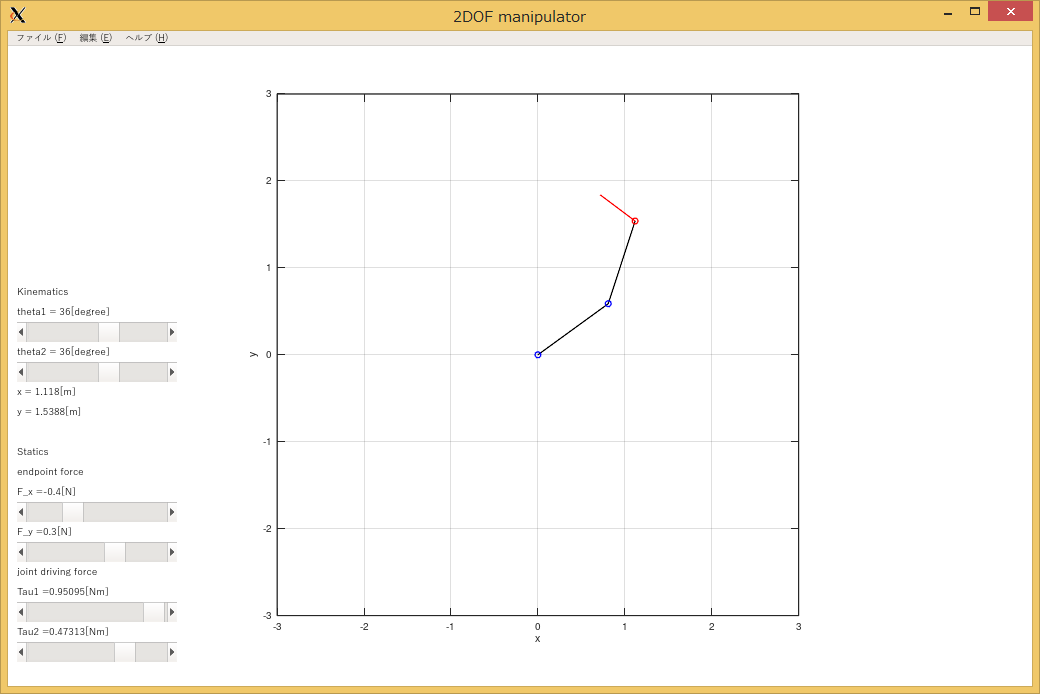
（ソースコード）

直線運動と回転運動

直線運動回転運動
変位 x[m]角度 θ[rad]
速度 v[m/s]角速度 ω[rad/s]
加速度 a[m/s2]角加速度 α[rad/s2]
力 f[N]トルク（モーメント） τ[Nm]
質量 m[kg]慣性モーメント I[kgm2]
粘性摩擦係数 c[N/(m/s)]粘性摩擦係数 cθ[Nm/(rad/s)]
弾性係数 k[N/m]弾性係数 kθ[Nm/rad]

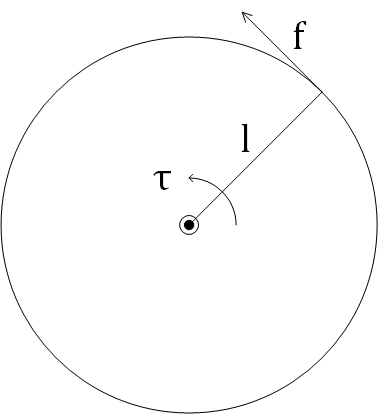
トルク（モーメント）\[ \tau=fl \]

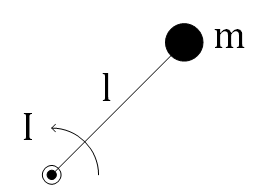
慣性モーメント\[ I=ml^2 \]

（直線運動の）運動方程式\[ ma + cv + kx = m\ddot x + c\dot x + kx = f \]

回転運動の運動方程式\[ I\alpha+c_\theta\omega+k_\theta\theta=I\ddot \theta+c_\theta\dot \theta+k_\theta\theta=\tau \]

平行軸の定理

I0は質量中心(CoM)まわりの慣性モーメント\[ I=I_0+ml^2 \]

慣性テンソル

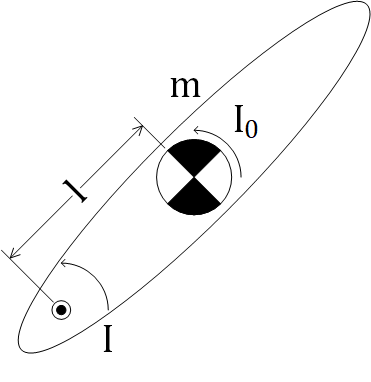
剛体の運動を３次元で記述するために必要になる。角運動量Lと角速度ωの関係は\(L=I\omega\)\[ \begin{bmatrix} L_x \\ L_y \\ L_z \end{bmatrix}=\begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{yx} & I_{yy} & -I_{yz} \\ -I_{zx} & -I_{zy} & I_{zz} \end{bmatrix}\begin{bmatrix} \omega_x \\ \omega_y \\ \omega_z \end{bmatrix} \]行列Iが慣性テンソル。行列の対角要素Ixx, Iyy, Izzが慣性モーメント。非対角要素Ixy=Iyx, Ixz=Izx, Iyz=Izyが慣性乗積

（慣性テンソルは正定対称行列になる）

動力学 (Dynamics)

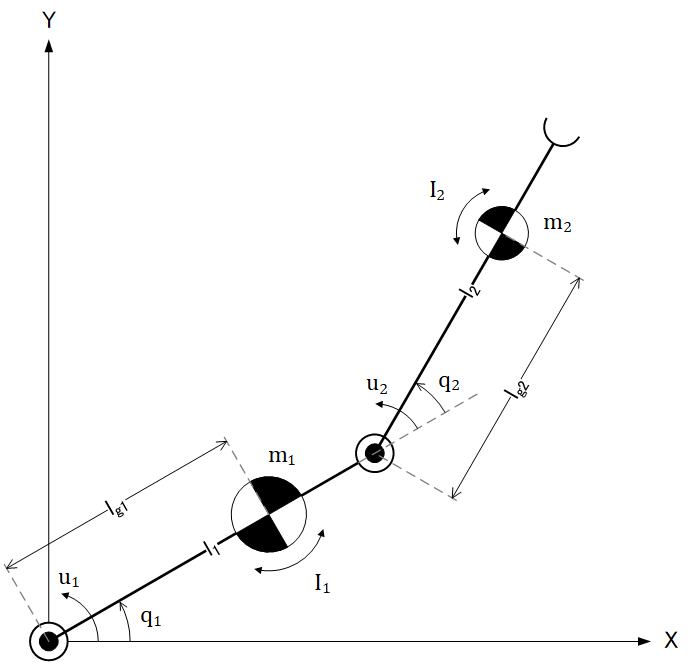
2リンクマニュピレータの運動方程式

  • 一般化座標 q1 q2
  • 一般化力 u1 u2

  • l1, l2: 各リンクの長さ
  • m1, m2: 各リンクの質量
  • I1, I2: 各リンクの質量中心まわりの慣性モーメント
  • lg1, lg2: 各リンクの関節から質量中心までの距離

Lagurangeの運動方程式

（解析力学より。）ラグランジュ法。考えている系(system)のエネルギーに着目する。

一般化座標と一般化力\[ q=\begin{bmatrix} q_1 \\ q_2 \\ \vdots \\ q_n \end{bmatrix},\quad u=\begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix} \]ロボットでは、一般化座標qは関節変数、一般化力uは関節駆動力（ロボットへの入力に相当する）。回転関節を有するロボットならば、関節角度と関節駆動トルク。

運動エネルギーの総和からポテンシャルエネルギーの総和を引いたものがラグラジアン（ラグランジアン）L

\[ L=\sum_{i=1}^{n}{K_i}-\sum_{i=1}^{n}{U_i} \]
  • L: ラグラジアン（ラグランジアン）
  • Ki：運動エネルギー
  • Ui: ポテンシャルエネルギー
  • n: 座標の数（＝ロボットのリンク数）

Lを求めたあと\[ \frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q_i}} \right)-\frac{\partial L}{\partial q_i}=u_i \]を計算することで（機械的に）運動方程式を立てることができる（計算機による記号計算で導出できる）。座標の数nだけ方程式が立つ（→ n本の方程式が出てくる）

（摩擦（粘性摩擦やクーロン摩擦）を考慮する場合には、これに散逸関数の項が加わる）

ラグランジアンLを求める

一般化座標と一般化力\[ q=\begin{bmatrix} \theta_1 \\ \theta_2 \end{bmatrix},\quad u=\begin{bmatrix} \tau_1 \\ \tau_2 \end{bmatrix} \]

位置（運動学）と速度。位置は、関節と手先の位置だけでなく、リンク質量中心の位置も考える。速度は、質量中心位置の速度が必要になる。（位置と速度の関係は、上記のヤコビ行列の速度の関係式より）

MaximaMATLAB Symbolic Math Toolbox
/* kinematics */
xg1: lg1*cos(th1)$
yg1: lg1*sin(th1)$
x1: l1*cos(th1)$
y1: l1*sin(th1)$
xg2: x1 + lg2*cos(th1 + th2)$
yg2: y1 + lg2*sin(th1 + th2)$

/* velocity of CoM */
/* dx1: diff(xg1, th1)*dth1$ */
/* dy1: diff(yg1, th1)*dth1$ */
dx2: diff(xg2, th1)*dth1 + diff(xg2, th2)*dth2$
dy2: diff(yg2, th1)*dth1 + diff(yg2, th2)*dth2$

/* v1: sqrt(dx1^2 + dy1^2)$ */
v2: sqrt(dx2^2 + dy2^2)$
 
% Robot parameter
syms l1 l2 m1 m2 I1 I2 lg1 lg2
syms th1 th2

% kinematics
syms x1 y1 xg1 yg1 xg2 yg2

xg1 = lg1*cos(th1);
yg1 = lg1*sin(th1);
x1 = l1*cos(th1);
y1 = l1*sin(th1);
xg2 = x1 + lg2*cos(th1 + th2);
yg2 = y1 + lg2*sin(th1 + th2);

% velocity of CoM
syms dx1 dy1 dx2 dy2 v1 v2
syms dth1 dth2

%dx1 = diff(xg1, th1)*dth1;
%dy1 = diff(yg1, th1)*dth1;
dx2 = diff(xg2, th1)*dth1 + diff(xg2, th2)*dth2;
dy2 = diff(yg2, th1)*dth1 + diff(yg2, th2)*dth2;

%v1 = sqrt(dx1^2 + dy1^2);
v2 = sqrt(dx2^2 + dy2^2);

速度は、用意されているjacobian()関数を使って求めることもできる。以下、リンク２の質量中心位置速度の例

Maxima（つづき）MATLAB Symbolic Math Toolbox（つづき）
jacobian([xg2, yg2], [th1, th2]) . matrix([dth1], [dth2]);
 
jacobian([xg2, yg2], [th1, th2])*[dth1; dth2]

（Maximaでドット演算子「 . 」は、行列の乗算）

運動エネルギーとポテンシャルエネルギー。運動エネルギーは質点の並進運動と剛体の回転運動の和（\( \frac{1}{2}mv^2 \)と\( \frac{1}{2}I\omega^2 \)を足したもの）。２リンク目の運動エネルギーは、１リンクの影響を込みで考える。

ポテンシャルエネルギー（\( mgh \)）は、基準をどこにとっているかに注意する。（どこから見た高さ\( h \)か。基準はどこにとってもよいが、決めた基準で一貫して計算する）

Maxima（つづき）MATLAB Symbolic Math Toolbox（つづき）
/* energy */
K1: 1/2*(m1*lg1^2 + I1)*dth1^2$
/* K1: 1/2*m1*v1^2 + 1/2*I1*dth1^2$ */
U1: m1*g*yg1$
K2: 1/2*m2*v2^2 + 1/2*I2*(dth1 + dth2)^2$
U2: m2*g*yg2$

K: K1 + K2$
U: U1 + U2$

/* Lagrangian */
L: K - U$
 
% energy
syms K1 U1 K2 U2 K U
syms g

K1 = 1/2*(m1*lg1^2 + I1)*dth1^2;
%K1 = 1/2*m1*v1^2 + 1/2*I1*dth1^2;
U1 = m1*g*yg1;
K2 = 1/2*m2*v2^2 + 1/2*I2*(dth1 + dth2)^2;
U2 = m2*g*yg2;

K = K1 + K2;
U = U1 + U2;

% Lagrangian
syms L

L = K - U;

運動方程式の導出

公式に従い、(\( \frac{\partial L}{\partial q_1} \), \( \frac{\partial L}{\partial q_2} \))、(\( \frac{\partial L}{\partial \dot q_1}\), \( \frac{\partial L}{\partial \dot q_2} \))、(\( \frac{d}{dt} \left( \frac{\partial L}{\partial \dot q_1} \right) \), \( \frac{d}{dt}\left( \frac{\partial L}{\partial \dot q_2} \right) \))を計算する。時間微分は全微分となる

Maxima（つづき）MATLAB Symbolic Math Toolbox（つづき）
/* Lagrange equation */
dLddth1: diff(L, dth1)$
dLddth2: diff(L, dth2)$

/* time derivative */
dt_dLddth1: diff(dLddth1, th1)*dth1 + diff(dLddth1, th2)*dth2 + diff(dLddth1, dth1)*ddth1 + diff(dLddth1, dth2)*ddth2$
dt_dLddth2: diff(dLddth2, th1)*dth1 + diff(dLddth2, th2)*dth2 + diff(dLddth2, dth1)*ddth1 + diff(dLddth2, dth2)*ddth2$

tau1: dt_dLddth1 - diff(L, th1)$
tau2: dt_dLddth2 - diff(L, th2)$

/* debug print */
fortran(ratsimp(tau1))$
fortran(ratsimp(tau2))$
tex(ratsimp(tau1))$
tex(ratsimp(tau2))$
 
% Lagrange equation
syms dLddth1 dLddth2 dt_dLddth1 dt_dLddth2 ddth1 ddth2 tau1 tau2

dLddth1 = diff(L, dth1);
dLddth2 = diff(L, dth2);

% time derivative
dt_dLddth1 = diff(dLddth1, th1)*dth1 + diff(dLddth1, th2)*dth2 + diff(dLddth1, dth1)*ddth1 + diff(dLddth1, dth2)*ddth2;
dt_dLddth2 = diff(dLddth2, th1)*dth1 + diff(dLddth2, th2)*dth2 + diff(dLddth2, dth1)*ddth1 + diff(dLddth2, dth2)*ddth2;

tau1 = dt_dLddth1 - diff(L, th1);
tau2 = dt_dLddth2 - diff(L, th2);

ロボットダイナミクスの一般形

ロボットの運動方程式を整理。２リンクマニピュレータ（２関節ロボット）の場合は２本の式が出てくる。それを行列とベクトルで表現する\[ M(q)\ddot q+h(q,\dot q)+g(q)=\tau \]Hを行列とする一般形で表現する場合もある\[ M(q)\ddot q+H(q,\dot q)\dot q+g(q)=\tau \]

関節の摩擦を考慮する場合には、左辺に\( D(\dot q) \)の項が加わる

Maxima（つづき）MATLAB Symbolic Math Toolbox（つづき）
/* M */
M11: ratsimp(coeff(tau1 - subst(0, ddth1, tau1), ddth1))$
M12: ratsimp(coeff(tau1 - subst(0, ddth2, tau1), ddth2))$
M21: ratsimp(coeff(tau2 - subst(0, ddth1, tau2), ddth1))$
M22: ratsimp(coeff(tau2 - subst(0, ddth2, tau2), ddth2))$

/* g */
g1: ratsimp(sublis([ddth1=0, ddth2=0, dth1=0, dth2=0], tau1))$
g2: ratsimp(sublis([ddth1=0, ddth2=0, dth1=0, dth2=0], tau2))$

/* h */
h1: ratsimp(tau1 - M11*ddth1 - M12*ddth2 - g1)$
h2: ratsimp(tau2 - M21*ddth1 - M22*ddth2 - g2)$

/* debug print */
fortran(M11)$
fortran(M12)$
fortran(M21)$
fortran(M22)$
fortran(h1)$
fortran(h2)$
fortran(g1)$
fortran(g2)$
tex(matrix([M11, M12], [M21, M22]))$
tex(matrix([h1], [h2]))$
tex(matrix([g1], [g2]))$
 
% M
M11 = collect(simplify(tau1 - subs(tau1, ddth1, 0)), ddth1);
M12 = collect(simplify(tau1 - subs(tau1, ddth2, 0)), ddth2);
M21 = collect(simplify(tau2 - subs(tau2, ddth1, 0)), ddth1);
M22 = collect(simplify(tau2 - subs(tau2, ddth2, 0)), ddth2);

% g
g1 = simplify(subs(tau1, {ddth1, ddth2, dth1, dth2}, {0, 0, 0, 0}));
g2 = simplify(subs(tau2, {ddth1, ddth2, dth1, dth2}, {0, 0, 0, 0}));

% h
h1 = simplify(tau1 - M11 - M12 - g1);
h2 = simplify(tau2 - M21 - M22 - g2);

% M
M11 = subs(M11, ddth1, 1);
M12 = subs(M12, ddth2, 1);
M21 = subs(M21, ddth1, 1);
M22 = subs(M22, ddth2, 1);

計算結果

Maxima
\( M(q) \) \[ \pmatrix{{\it lg}_{2}^2\,m_{2}\,\sin ^2\left({\it th}_{2}+ {\it th}_{1}\right)+2\,l_{1}\,{\it lg}_{2}\,m_{2}\,\sin {\it th}_{1} \,\sin \left({\it th}_{2}+{\it th}_{1}\right)+{\it lg}_{2}^2\,m_{2} \,\cos ^2\left({\it th}_{2}+{\it th}_{1}\right)+2\,l_{1}\, {\it lg}_{2}\,m_{2}\,\cos {\it th}_{1}\,\cos \left({\it th}_{2}+ {\it th}_{1}\right)+l_{1}^2\,m_{2}\,\sin ^2{\it th}_{1}+l_{1}^2\, m_{2}\,\cos ^2{\it th}_{1}+{\it lg}_{1}^2\,m_{1}+I_{2}+I_{1}& {\it lg}_{2}^2\,m_{2}\,\sin ^2\left({\it th}_{2}+{\it th}_{1}\right) +l_{1}\,{\it lg}_{2}\,m_{2}\,\sin {\it th}_{1}\,\sin \left( {\it th}_{2}+{\it th}_{1}\right)+{\it lg}_{2}^2\,m_{2}\,\cos ^2 \left({\it th}_{2}+{\it th}_{1}\right)+l_{1}\,{\it lg}_{2}\,m_{2}\, \cos {\it th}_{1}\,\cos \left({\it th}_{2}+{\it th}_{1}\right)+I_{2} \cr {\it lg}_{2}^2\,m_{2}\,\sin ^2\left({\it th}_{2}+{\it th}_{1} \right)+l_{1}\,{\it lg}_{2}\,m_{2}\,\sin {\it th}_{1}\,\sin \left( {\it th}_{2}+{\it th}_{1}\right)+{\it lg}_{2}^2\,m_{2}\,\cos ^2 \left({\it th}_{2}+{\it th}_{1}\right)+l_{1}\,{\it lg}_{2}\,m_{2}\, \cos {\it th}_{1}\,\cos \left({\it th}_{2}+{\it th}_{1}\right)+I_{2} &{\it lg}_{2}^2\,m_{2}\,\sin ^2\left({\it th}_{2}+{\it th}_{1} \right)+{\it lg}_{2}^2\,m_{2}\,\cos ^2\left({\it th}_{2}+ {\it th}_{1}\right)+I_{2}\cr } \]
\( h(q,\dot q) \) \[ \pmatrix{\left(-{\it dth}_{2}^2-2\,{\it dth}_{1}\,{\it dth}_{2} \right)\,l_{1}\,{\it lg}_{2}\,m_{2}\,\cos {\it th}_{1}\,\sin \left( {\it th}_{2}+{\it th}_{1}\right)+\left({\it dth}_{2}^2+2\, {\it dth}_{1}\,{\it dth}_{2}\right)\,l_{1}\,{\it lg}_{2}\,m_{2}\, \sin {\it th}_{1}\,\cos \left({\it th}_{2}+{\it th}_{1}\right)\cr {\it dth}_{1}^2\,l_{1}\,{\it lg}_{2}\,m_{2}\,\cos {\it th}_{1}\, \sin \left({\it th}_{2}+{\it th}_{1}\right)-{\it dth}_{1}^2\,l_{1}\, {\it lg}_{2}\,m_{2}\,\sin {\it th}_{1}\,\cos \left({\it th}_{2}+ {\it th}_{1}\right)\cr } \]
\( g(q) \) \[ \pmatrix{g\,{\it lg}_{2}\,m_{2}\,\cos \left({\it th}_{2}+ {\it th}_{1}\right)+\left(g\,l_{1}\,m_{2}+g\,{\it lg}_{1}\,m_{1} \right)\,\cos {\it th}_{1}\cr g\,{\it lg}_{2}\,m_{2}\,\cos \left( {\it th}_{2}+{\it th}_{1}\right)\cr } \]

（Maximaのratsimp()とSymbolic Math Toolboxのsimplify()の差により式の形が違っている。→ 追記）

MATLAB Symbolic Math Toolbox
\( M(q) \) \[ \begin{bmatrix} m_2*l_1^2 + 2*m_2*\cos(th_2)*l_1*lg_2 + m_1*lg_1^2 + m_2*lg_2^2 + I_1 + I_2 & m_2*lg_2^2 + l_1*m_2*\cos(th_2)*lg_2 + I_2 \\ m_2*lg_2^2 + l_1*m_2*\cos(th_2)*lg_2 + I_2 & m_2*lg_2^2 + I_2 \end{bmatrix} \]
\( h(q,\dot q) \) \[ \begin{bmatrix} -dth_2*l_1*lg_2*m_2*\sin(th_2)*(2*dth_1 + dth_2) \\ dth_1^2*l_1*lg_2*m_2*\sin(th_2) \end{bmatrix} \]
\( g(q) \) \[ \begin{bmatrix} g*m_2*(lg_2*cos(th_1 + th_2) + l_1*cos(th_1)) + g*lg_1*m_1*cos(th_1) \\ g*lg_2*m_2*cos(th_1 + th_2) \end{bmatrix} \]

運動方程式の比較、確認

MATLAB Symbolic Math Toolbox（つづき）
% compare to verify
simplify(M11 - (2*l1*lg2*m2*cos(th2)+lg2^2*m2+l1^2*m2+lg1^2*m1+I2+I1))
simplify(M12 - (l1*lg2*m2*cos(th2)+lg2^2*m2+I2))
simplify(M21 - (l1*lg2*m2*cos(th2)+lg2^2*m2+I2))
simplify(M22 - (lg2^2*m2+I2))

simplify(h1 - (-dth2*(dth2+2*dth1)*l1*lg2*m2*sin(th2)))
simplify(h2 - (dth1^2*l1*lg2*m2*sin(th2)))

simplify(g1 - (g*m2*(lg2*cos(th2+th1)+l1*cos(th1))+g*lg1*m1*cos(th1)))
simplify(g2 - (g*lg2*m2*cos(th2+th1)))
 
% another way
simplify(M11 == (2*l1*lg2*m2*cos(th2)+lg2^2*m2+l1^2*m2+lg1^2*m1+I2+I1))
simplify(M12 == (l1*lg2*m2*cos(th2)+lg2^2*m2+I2))
simplify(M21 == (l1*lg2*m2*cos(th2)+lg2^2*m2+I2))
simplify(M22 == (lg2^2*m2+I2))

simplify(h1 == (-dth2*(dth2+2*dth1)*l1*lg2*m2*sin(th2)))
simplify(h2 == (dth1^2*l1*lg2*m2*sin(th2)))

simplify(g1 == (g*m2*(lg2*cos(th2+th1)+l1*cos(th1))+g*lg1*m1*cos(th1)))
simplify(g2 == (g*lg2*m2*cos(th2+th1)))

同様にして、教科書などにある運動方程式と比較して確認。（座標系のとり方が違うと同じ運動方程式にならないので、他人（ひと）の運動方程式を見るときには注意）

得られた運動方程式\[ \begin{bmatrix} m_2 l_1^2 + 2 m_2 \cos(\theta_2) l_1 l_{g2} + m_1 l_{g1}^2 + m_2 l_{g2}^2 + I_1 + I_2 & m_2 l_{g2}^2 + l_1 m_2 \cos(\theta_2) l_{g2} + I_2 \\ m_2 l_{g2}^2 + l_1 m_2 \cos(\theta_2) l_{g2} + I_2 & m_2 l_{g2}^2 + I_2 \end{bmatrix} \begin{bmatrix} \ddot\theta_1 \\ \ddot\theta_2 \end{bmatrix} + \begin{bmatrix} -\dot\theta_2 l_1 l_{g2} m_2 \sin(\theta_2) (2 \dot\theta_1 + \dot\theta_2) \\ \dot\theta_1^2 l_1 l_{g2} m_2 \sin(\theta_2) \end{bmatrix} + \begin{bmatrix} g m_2 (l_{g2} \cos(\theta_1 + \theta_2) + l_1 \cos(\theta_1)) + g l_{g1} m_1 \cos(\theta_1) \\ g l_{g2} m_2 \cos(\theta_1 + \theta_2) \end{bmatrix} = \begin{bmatrix} \tau_1 \\ \tau_2 \end{bmatrix} \]角加速度に関連した項、角速度に関連した項、重力加速度gを含んだ項の３つに整理できている。（ratsimp()よりsimplify()の方が簡素な式が出てくるので、Symbolic Math Toolboxで生成した式を採用 → 追記）

使用したソフトウェアのバージョン

Maximaによる運動方程式の簡略化《追記》

Maximaでは、三角関数縮小のためのtrigreduce()関数が別途用意されている

Maxima（再掲載）
/* kinematics */
xg1: lg1*cos(th1)$
yg1: lg1*sin(th1)$
x1: l1*cos(th1)$
y1: l1*sin(th1)$
xg2: x1 + lg2*cos(th1 + th2)$
yg2: y1 + lg2*sin(th1 + th2)$

/* velocity of CoM */
/* dx1: diff(xg1, th1)*dth1$ */
/* dy1: diff(yg1, th1)*dth1$ */
dx2: diff(xg2, th1)*dth1 + diff(xg2, th2)*dth2$
dy2: diff(yg2, th1)*dth1 + diff(yg2, th2)*dth2$

/* v1: sqrt(dx1^2 + dy1^2)$ */
v2: sqrt(dx2^2 + dy2^2)$

/* energy */
K1: 1/2*(m1*lg1^2 + I1)*dth1^2$
/* K1: 1/2*m1*v1^2 + 1/2*I1*dth1^2$ */
U1: m1*g*yg1$
K2: 1/2*m2*v2^2 + 1/2*I2*(dth1 + dth2)^2$
U2: m2*g*yg2$

K: K1 + K2$
U: U1 + U2$

/* Lagrangian */
L: K - U$

/* Lagrange equation */
dLddth1: diff(L, dth1)$
dLddth2: diff(L, dth2)$

/* time derivative */
dt_dLddth1: diff(dLddth1, th1)*dth1 + diff(dLddth1, th2)*dth2 + diff(dLddth1, dth1)*ddth1 + diff(dLddth1, dth2)*ddth2$
dt_dLddth2: diff(dLddth2, th1)*dth1 + diff(dLddth2, th2)*dth2 + diff(dLddth2, dth1)*ddth1 + diff(dLddth2, dth2)*ddth2$

tau1: dt_dLddth1 - diff(L, th1)$
tau2: dt_dLddth2 - diff(L, th2)$

ratsimp()関数ではなく、trigreduce()関数を用いて書き直す

Maxima（つづき）
/* M */
M11: trigreduce(coeff(tau1 - subst(0, ddth1, tau1), ddth1))$
M12: trigreduce(coeff(tau1 - subst(0, ddth2, tau1), ddth2))$
M21: trigreduce(coeff(tau2 - subst(0, ddth1, tau2), ddth1))$
M22: trigreduce(coeff(tau2 - subst(0, ddth2, tau2), ddth2))$

/* g */
g1: trigreduce(sublis([ddth1=0, ddth2=0, dth1=0, dth2=0], tau1))$
g2: trigreduce(sublis([ddth1=0, ddth2=0, dth1=0, dth2=0], tau2))$

/* h */
h1: trigreduce(tau1 - M11*ddth1 - M12*ddth2 - g1)$
h2: trigreduce(tau2 - M21*ddth1 - M22*ddth2 - g2)$

/* debug print */
tex(matrix([M11, M12], [M21, M22]))$
tex(matrix([h1], [h2]))$
tex(matrix([g1], [g2]))$

Maximaで再計算した、計算結果

Maxima（再計算）
\( M(q) \) \[\pmatrix{{\it I_2}+{\it I_1}+2\,{\it l_1}\,{\it lg_2}\,{\it m_2}\, \cos {\it th_2}+\left({\it l_1}^2+{\it lg_2}^2\right)\,{\it m_2}+ {\it lg_1}^2\,{\it m_1}&{\it I_2}+{\it l_1}\,{\it lg_2}\,{\it m_2}\, \cos {\it th_2}+{\it lg_2}^2\,{\it m_2}\cr {\it I_2}+{\it l_1}\, {\it lg_2}\,{\it m_2}\,\cos {\it th_2}+{\it lg_2}^2\,{\it m_2}& {\it I_2}+{\it lg_2}^2\,{\it m_2}\cr }\]
\( h(q,\dot q) \) \[\pmatrix{\left(-{\it dth_2}^2-2\,{\it dth_1}\,{\it dth_2}\right)\, {\it l_1}\,{\it lg_2}\,{\it m_2}\,\sin {\it th_2}\cr \left( {\it dth_1}^2+{\it dth_1}\,{\it dth_2}\right)\,{\it l_1}\,{\it lg_2} \,{\it m_2}\,\sin {\it th_2}-{\it dth_1}\,{\it dth_2}\,{\it l_1}\, {\it lg_2}\,{\it m_2}\,\sin {\it th_2}\cr }\]
\( g(q) \) \[\pmatrix{g\,{\it lg_2}\,{\it m_2}\,\cos \left({\it th_1}+{\it th_2} \right)+g\,{\it l_1}\,{\it m_2}\,\cos {\it th_1}+g\,{\it lg_1}\, {\it m_1}\,\cos {\it th_1}\cr g\,{\it lg_2}\,{\it m_2}\,\cos \left( {\it th_1}+{\it th_2}\right)\cr }\]

Symbolic Math Toolboxのsimplify()関数と同様の、簡略化された式がMaximaでも得られる

ロボットアームのシミュレーション

非線形な微分方程式を数値計算で解く

ロボットの運動方程式を、２階の微分方程式から１階の微分方程式に変換する\[ \frac{d}{dt}\begin{bmatrix} \dot\theta \\ \theta \end{bmatrix}=\begin{bmatrix} M^{-1}(\theta)\left(\tau - h(\theta, \dot\theta) - g(\theta)\right) \\ \dot \theta \end{bmatrix} \]これを解けばよい

常微分方程式の解を求めるために、提供されているODE(Ordinary Differential Equation)のソルバーを利用する

Octave lsodePython odeint
clear all; clc;

%% dynamics
function dxdt = robot_dynamics(x, t)
  global l1; global l2;
  global lg1; global lg2;
  global m1; global m2;
  global I1; global I2;
  global g;

  th1 = x(1); th2 = x(2); dth1 = x(3); dth2 = x(4);

  tau1 = 0.0; % [N m]
  tau2 = 0.0; % [N m]

  M11 = m2*l1^2 + 2*m2*cos(th2)*l1*lg2 + m1*lg1^2 + m2*lg2^2 + I1 + I2;
  M12 = m2*lg2^2 + l1*m2*cos(th2)*lg2 + I2;
  M21 = m2*lg2^2 + l1*m2*cos(th2)*lg2 + I2;
  M22 = m2*lg2^2 + I2;
  M = [M11 M12; M21 M22];

  h1 = -dth2*l1*lg2*m2*sin(th2)*(2*dth1 + dth2);
  h2 = dth1^2*l1*lg2*m2*sin(th2);

  g1 = g*m2*(lg2*cos(th1 + th2) + l1*cos(th1)) + g*lg1*m1*cos(th1);
  g2 = g*lg2*m2*cos(th1 + th2);

  tmp = inv(M)*([tau1; tau2] - [h1; h2] - [g1; g2]);
  ddth1 = tmp(1);
  ddth2 = tmp(2);

  dxdt = [dth1, dth2, ddth1, ddth2];
end

%% parameters
global l1 = 1.0; % [m]
global l2 = 1.0; % [m]
global lg1 = 0.5; % [m]
global lg2 = 0.5; % [m]
global m1 = 1.0; % [kg]
global m2 = 1.0; % [kg]
global I1 = 0.1; % [kg m^2]
global I2 = 0.1; % [kg m^2]

global g = 9.8; % [m/s^2]

%% initial value
th1 = 30*(pi/180); % [rad]
th2 = 30*(pi/180); % [rad]
dth1 = 0.0; % [rad/s]
dth2 = 0.0; % [rad/s]

x = [th1, th2, dth1, dth2];

t = linspace(0, 10, 1001);
% t = linspace(0, 10, 101);

y = lsode('robot_dynamics', x, t);
import numpy as np
from scipy.integrate import odeint

# dynamics
def robot_dynamics(x, t):
  global l1, l2
  global lg1, lg2
  global m1, m2
  global I1, I2
  global g

  th1 = x[0]; th2 = x[1]; dth1 = x[2]; dth2 = x[3]

  tau1 = 0.0 # [N m]
  tau2 = 0.0 # [N m]

  M11 = m2*l1**2 + 2*m2*np.cos(th2)*l1*lg2 + m1*lg1**2 + m2*lg2**2 + I1 + I2
  M12 = m2*lg2**2 + l1*m2*np.cos(th2)*lg2 + I2
  M21 = m2*lg2**2 + l1*m2*np.cos(th2)*lg2 + I2
  M22 = m2*lg2**2 + I2
  M = np.array([[M11, M12], [M21, M22]])

  h1 = -dth2*l1*lg2*m2*np.sin(th2)*(2*dth1 + dth2)
  h2 = dth1**2*l1*lg2*m2*np.sin(th2)

  g1 = g*m2*(lg2*np.cos(th1 + th2) + l1*np.cos(th1)) + g*lg1*m1*np.cos(th1)
  g2 = g*lg2*m2*np.cos(th1 + th2)

  tmp = np.linalg.inv(M)*(np.array([[tau1], [tau2]]) - np.array([[h1], [h2]]) - np.array([[g1], [g2]]))
  ddth1 = tmp[0, 0]
  ddth2 = tmp[1, 0]

  dxdt = [dth1, dth2, ddth1, ddth2]
  return dxdt

if __name__ == '__main__':
  # parameters
  l1 = 1.0 # [m]
  l2 = 1.0 # [m]
  lg1 = 0.5 # [m]
  lg2 = 0.5 # [m]
  m1 = 1.0 # [kg]
  m2 = 1.0 # [kg]
  I1 = 0.1 # [kg m^2]
  I2 = 0.1 # [kg m^2]

  g = 9.8 # [m/s^2]

  # initial value
  th1 = 30*(np.pi/180) # [rad]
  th2 = 30*(np.pi/180) # [rad]
  dth1 = 0.0 # [rad/s]
  dth2 = 0.0 # [rad/s]

  x = [th1, th2, dth1, dth2]

  t = np.linspace(0, 10, 101)

  y = odeint(robot_dynamics, x, t)

シミュレーション結果からアニメーションを作成

Octave（つづき）Python（つづき）
%% animation
for i=1:length(t)
  th1 = y(i,1); th2 = y(i,2);
  joint0 = [0, 0];
  joint1 = [l1*cos(th1), l1*sin(th1)];
  joint2 = [joint1(1)+l2*cos(th1+th2), joint1(2)+l2*sin(th1+th2)];
  plot([joint0(1), joint1(1)], [joint0(2), joint1(2)], 'o-', 'linewidth', 5);
  hold on;
  plot([joint1(1), joint2(1)], [joint1(2), joint2(2)], '-', 'linewidth', 5);
  axis equal; axis([-2.2, 2.2, -2.2, 2.2]); grid;
  title(sprintf('%5.2f [s]', t(i)));
  hold off;
  drawnow;
  % pause;
  % print(strcat('sim', num2str(i - 1, '%04d'), '.png'), '-dpng');
end
import matplotlib.pyplot as plt

if __name__ == '__main__':
  # animation
  plt.style.use('ggplot')

  for i in range(0, len(t)):
    th1 = y[i,0]; th2 = y[i,1]
    joint0 = [0, 0]
    joint1 = [l1*np.cos(th1), l1*np.sin(th1)]
    joint2 = [joint1[0]+l2*np.cos(th1+th2), joint1[1]+l2*np.sin(th1+th2)]
    plt.clf()
    plt.plot([joint0[0], joint1[0]], [joint0[1], joint1[1]], marker='o', linewidth=5)
    plt.plot([joint1[0], joint2[0]], [joint1[1], joint2[1]], linewidth=5)
    plt.xlim([-2.2, 2.2]); plt.ylim([-2.2, 2.2])
    plt.title(format(t[i], '5.2f') + ' [s]')
    # plt.show()
    plt.savefig('sim' + format(i, '04d') + '.png')
ImageMagick
$ convert -delay 1 -loop 0 sim*.png anime.gif

導出したロボットの運動方程式の解

ロボットダイナミクスの性質

\( M(q) \)の項は、\( M_{12} \)と\( M_{21} \)が必ず同じになる。関節変数\( \theta_2 \)があり、\( \cos(\theta_2) \)なので、\( \theta_2 \)が0のとき（一番腕を伸ばしているとき）に一番大きな慣性力が働く。

\( h(q, \dot q) \)の項は、直動関節だけを持つロボットの運動方程式を立てると無くなる。角速度の二乗に比例する力は、遠心力。異なる角速度の積の項は、コリオリ力。

\( g(q) \)の項は、重力の作用しない宇宙空間で運動方程式を立てると無くなる。

ほか

《積み残し》

運動学と静力学と動力学の関係

全体図

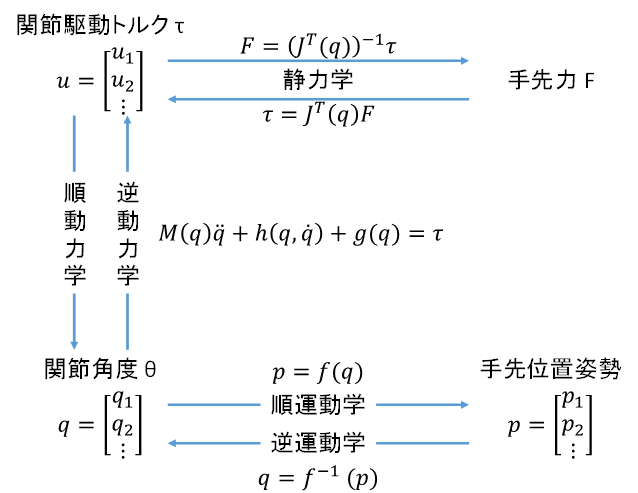
（逆動力学の問題（ロボットを目標の姿勢にするためにどれだけの関節駆動トルクτを発生させればよいか）を解くためには、制御の力を借りる）

リアプノフの安定論、リアプノフ関数

《積み残し》

LaSalleの定理

《積み残し》

ロボットの制御

計算トルク法、PID制御など。目標軌道生成について

《積み残し》

位置と力のハイブリッド制御

《積み残し》

コンプライアンス制御、インピーダンス制御

《積み残し》

冗長関節

《積み残し》

参考文献

© 2018 Tadakazu Nagai