コンピュータビジョン

永井忠一 2019.7.28

ピンホールカメラモデル(Pinhole camera model)

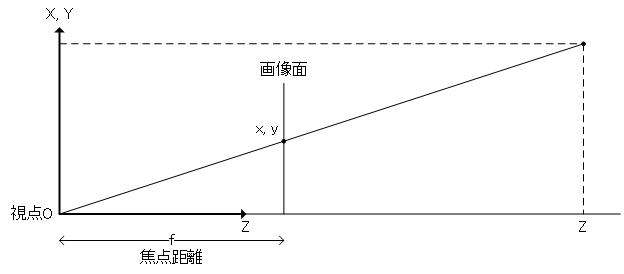
ピンホールカメラの式。fは焦点距離。（比例）\[ x = f\frac{X}{Z}, y = f\frac{Y}{Z} \]

入力はX, Y, Zの３次元。出力はx, yの２次元。（射影変換）

平行ステレオ

視差(disparity): x₁ - x₂
カメラ間の距離(baseline length): d
焦点距離: f
対象までの距離: Z

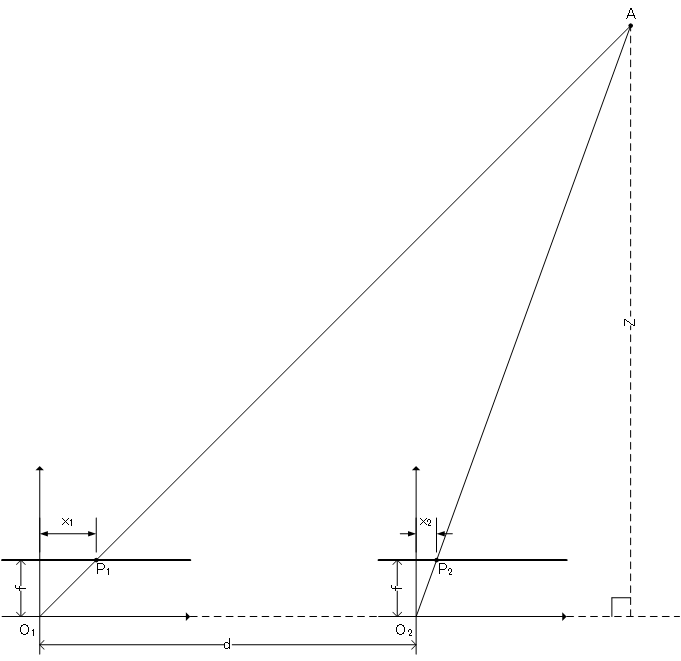
△AO₁O₂と△AP₁P₂の相似\[ \overline{O_{1}O_{2}}:\overline{P_{1}P_{2}}=Z:(Z-f) \]\[ d:(d-x_{1}+x_{2})=Z:(Z-f) \]

（比の性質）\[ d(Z-f)=Z(d-x_{1}+x_{2}) \]

（Zについて整理）\[ dZ-df=Z(d-x_{1}+x_{2}) \]\[ -df=-Zx_{1}+Zx_{2} \]\[ -df=Z(-x_{1}+x_{2}) \]\[ \therefore Z=\frac{fd}{x_{1}-x_{2}} \]

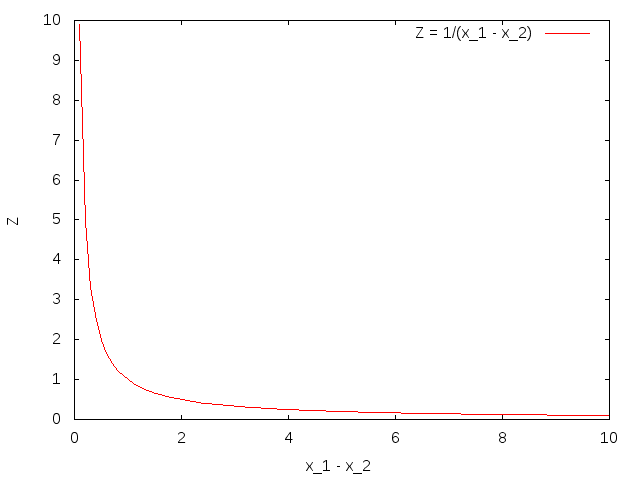
視差(disparity)と距離の関係は反比例。

カメラ座標系と世界座標系の関係

座標変換（回転行列と同次座標表現）

クォータニオン(Quaternion)

（単位四元数を使って３次元空間の回転を表す）

回転軸\[ \mathbf{n}=\left( \begin{array}{c} n_1 \\ n_2 \\ n_3 \end{array} \right) \]ただしnは単位ベクトル

回転角θ\[ \dot{q}=\cos{\frac{\theta}{2}}+\sin{\frac{\theta}{2}n_1}i+\sin{\frac{\theta}{2}n_2}j+\sin{\frac{\theta}{2}n_3}k=\left( \begin{array}{c} \cos{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}n_1} \\ \sin{\frac{\theta}{2}n_2} \\ \sin{\frac{\theta}{2}n_3} \end{array} \right) \]

点(x, y, z) \[ \mathbf{\dot{r}}=xi+yj+zk=\left( \begin{array}{c} 0 \\ x \\ y \\ z \end{array} \right) \]\(\mathbf{\dot{r}}\)は純虚

回転\[ \dot{q}\mathbf{\dot{r}}\dot{q}^{*}=\left( \begin{array}{c} \cos{\frac{\theta}{2}} \\ \sin{\frac{\theta}{2}n_1} \\ \sin{\frac{\theta}{2}n_2} \\ \sin{\frac{\theta}{2}n_3} \end{array} \right) \left( \begin{array}{c} 0 \\ x \\ y \\ z \end{array} \right) \left( \begin{array}{c} \cos{\frac{\theta}{2}} \\ -\sin{\frac{\theta}{2}n_1} \\ -\sin{\frac{\theta}{2}n_2} \\ -\sin{\frac{\theta}{2}n_3} \end{array} \right) \]\( \dot{q}^{*} \)は共役クォータニオン

四元数(Quaternion)による回転の例

Z軸まわりに60度回転する四元数\[ \cos{\frac{60^\circ}{2}}+\sin{\frac{60^\circ}{2}}\times{0}i+\sin{\frac{60^\circ}{2}}\times0j+\sin{\frac{60^\circ}{2}}\times1k\\=\frac{\sqrt{3}}{2}+\frac{1}{2}k \]

(1, 0, 0)を上記の四元数で回転させる

\[ (\frac{\sqrt 3}{2}+\frac{1}{2}k)i(\frac{\sqrt 3}{2}-\frac{1}{2}k) \]
\[ =(\frac{\sqrt 3}{2}+\frac{1}{2}k)(\frac{\sqrt 3}{2}i-\frac{1}{2}ik) \]	虚数単位と虚数単位が掛かってik=-j
\[ =\frac{\sqrt 3}{2}\frac{\sqrt 3}{2}i+\frac{\sqrt 3}{2}\frac{1}{2}j+\frac{1}{2}\frac{\sqrt 3}{2}ki+\frac{1}{2}\frac{1}{2}kj \]	虚数単位と虚数単位が掛かってki=j, kj=-i
\[ =(\frac{\sqrt 3}{2}\frac{\sqrt 3}{2}-\frac{1}{2}\frac{1}{2})i+(\frac{\sqrt 3}{2}\frac{1}{2}+\frac{1}{2}\frac{\sqrt 3}{2})j \]
\[ =\frac{1}{2}i+\frac{\sqrt 3}{2}j \]

OctaveのQuaternionパッケージ

Linux

Linux
`$ sudo apt install octave-quaternion`
`octave:1> pkg list Package Name \| Version \| Installation directory --------------+---------+----------------------- quaternion \| 2.4.0 \| /usr/share/octave/packages/quaternion-2.4.0`

$ sudo apt install octave-quaternion

octave:1> pkg list
Package Name  | Version | Installation directory
--------------+---------+-----------------------
  quaternion  |   2.4.0 | /usr/share/octave/packages/quaternion-2.4.0

OctaveとWolfram言語でQuaternion

Octave Wolfram

Octave	Wolfram
`octave:2> pkg load quaternion octave:3> q = quaternion(cos(pi/6), 0, 0, sin(pi/6)) q = 0.866 + 0i + 0j + 0.5k octave:4> r = quaternion(0, 1, 0, 0) r = 0 + 1i + 0j + 0k octave:5> q * r * conj(q) ans = 0 + 0.5i + 0.866j + 0k`	`Quaternion[cos(pi/6), 0, 0, sin(pi/6)] * Quaternion[0, 1, 0, 0] * Quaternion[cos(pi/6), 0, 0, -sin(pi/6)]`

octave:2> pkg load quaternion
octave:3> q = quaternion(cos(pi/6), 0, 0, sin(pi/6))
q = 0.866 + 0i + 0j + 0.5k
octave:4> r = quaternion(0, 1, 0, 0)
r = 0 + 1i + 0j + 0k
octave:5> q * r * conj(q)
ans = 0 + 0.5i + 0.866j + 0k

Quaternion[cos(pi/6), 0, 0, sin(pi/6)] * Quaternion[0, 1, 0, 0] * Quaternion[cos(pi/6), 0, 0, -sin(pi/6)]

（回転を表すのはノルムが１の単位四元数）

Octave	Wolfram
`octave:1> pkg load quaternion octave:2> q = quaternion(cos(pi/6), 0, 0, sin(pi/6)) q = 0.866 + 0i + 0j + 0.5k octave:3> norm(q) ans = 1`	`Norm[Quaternion[cos(pi/6), 0, 0, sin(pi/6)]]`

空間フィルタリング

畳み込み\[ B={A}\otimes{h} \]

hというフィルタをかける（画像では非対称なフィルタは使わない）

加重平均フィルタ

平滑化（ローパスフィルタ）

２次元ガウス分布(Gaussian)

3x3画素
\( \frac{1}{16} \)	\( \frac{2}{16} \)	\( \frac{1}{16} \)
\( \frac{2}{16} \)	\( \frac{4}{16} \)	\( \frac{2}{16} \)
\( \frac{1}{16} \)	\( \frac{2}{16} \)	\( \frac{1}{16} \)

5x5画素
\( \frac{1}{256} \)	\( \frac{4}{256} \)	\( \frac{6}{256} \)	\( \frac{4}{256} \)	\( \frac{1}{256} \)
\( \frac{4}{256} \)	\( \frac{16}{256} \)	\( \frac{24}{256} \)	\( \frac{16}{256} \)	\( \frac{4}{256} \)
\( \frac{6}{256} \)	\( \frac{24}{256} \)	\( \frac{36}{256} \)	\( \frac{24}{256} \)	\( \frac{6}{256} \)
\( \frac{4}{256} \)	\( \frac{16}{256} \)	\( \frac{24}{256} \)	\( \frac{16}{256} \)	\( \frac{4}{256} \)
\( \frac{1}{256} \)	\( \frac{4}{256} \)	\( \frac{6}{256} \)	\( \frac{4}{256} \)	\( \frac{1}{256} \)

C/C++

C/C++
#include <stdint.h> static uint8_t gaussian_3x3(const uint8_t y[3][3]) { return (((1 * y[0][0]) + (2 * y[0][1]) + (1 * y[0][2]) + (2 * y[1][0]) + (4 * y[1][1]) + (2 * y[1][2]) + (1 * y[2][0]) + (2 * y[2][1]) + (1 * y[2][2])) / 16); } static uint8_t gaussian_5x5(const uint8_t y[5][5]) { return ((( 2 * y[0][0]) + ( 7 * y[0][1]) + ( 12 * y[0][2]) + ( 7 * y[0][3]) + ( 2 * y[0][4]) + ( 7 * y[1][0]) + (31 * y[1][1]) + ( 52 * y[1][2]) + (31 * y[1][3]) + ( 7 * y[1][4]) + (12 * y[2][0]) + (52 * y[2][1]) + (127 * y[2][2]) + (52 * y[2][3]) + (12 * y[2][4]) + ( 7 * y[3][0]) + (31 * y[3][1]) + ( 52 * y[3][2]) + (31 * y[3][3]) + ( 7 * y[3][4]) + ( 2 * y[4][0]) + ( 7 * y[4][1]) + ( 12 * y[4][2]) + ( 7 * y[4][3]) + ( 2 * y[4][4])) / 571); }
Python
def clip(fp): if fp > 255: fp = 255 elif fp < 0: fp = 0 return fp def kernel_gauss(p_5x5): fp = ((1/256)p_5x5[0][0] + (4/256)p_5x5[0][1] + (6/256)p_5x5[0][2] + (4/256)p_5x5[0][3] + (1/256)p_5x5[0][4] \ + (4/256)p_5x5[1][0] + (16/256)p_5x5[1][1] + (24/256)p_5x5[1][2] + (16/256)p_5x5[1][3] + (4/256)p_5x5[1][4] \ + (6/256)p_5x5[2][0] + (24/256)p_5x5[2][1] + (36/256)p_5x5[2][2] + (24/256)p_5x5[2][3] + (16/256)p_5x5[2][4] \ + (4/256)p_5x5[3][0] + (16/256)p_5x5[3][1] + (24/256)p_5x5[3][2] + (16/256)p_5x5[3][3] + (4/256)p_5x5[3][4] \ + (1/256)p_5x5[4][0] + (4/256)p_5x5[4][1] + (6/256)p_5x5[4][2] + (4/256)p_5x5[4][3] + (1/256)*p_5x5[4][4]) return int(clip(fp))

#include <stdint.h>

static uint8_t gaussian_3x3(const uint8_t y[3][3]) {
        return (((1 * y[0][0]) + (2 * y[0][1]) + (1 * y[0][2]) +
                 (2 * y[1][0]) + (4 * y[1][1]) + (2 * y[1][2]) +
                 (1 * y[2][0]) + (2 * y[2][1]) + (1 * y[2][2])) / 16);
}

static uint8_t gaussian_5x5(const uint8_t y[5][5]) {
        return ((( 2 * y[0][0]) + ( 7 * y[0][1]) + ( 12 * y[0][2]) + ( 7 * y[0][3]) + ( 2 * y[0][4]) +
                 ( 7 * y[1][0]) + (31 * y[1][1]) + ( 52 * y[1][2]) + (31 * y[1][3]) + ( 7 * y[1][4]) +
                 (12 * y[2][0]) + (52 * y[2][1]) + (127 * y[2][2]) + (52 * y[2][3]) + (12 * y[2][4]) +
                 ( 7 * y[3][0]) + (31 * y[3][1]) + ( 52 * y[3][2]) + (31 * y[3][3]) + ( 7 * y[3][4]) +
                 ( 2 * y[4][0]) + ( 7 * y[4][1]) + ( 12 * y[4][2]) + ( 7 * y[4][3]) + ( 2 * y[4][4])) / 571);
}

Python

def clip(fp):
    if fp > 255:
        fp = 255
    elif fp < 0:
        fp = 0
    return fp

def kernel_gauss(p_5x5):
    fp = ((1/256)*p_5x5[0][0] + (4/256)*p_5x5[0][1] + (6/256)*p_5x5[0][2] + (4/256)*p_5x5[0][3] + (1/256)*p_5x5[0][4] \
          + (4/256)*p_5x5[1][0] + (16/256)*p_5x5[1][1] + (24/256)*p_5x5[1][2] + (16/256)*p_5x5[1][3] + (4/256)*p_5x5[1][4] \
          + (6/256)*p_5x5[2][0] + (24/256)*p_5x5[2][1] + (36/256)*p_5x5[2][2] + (24/256)*p_5x5[2][3] + (16/256)*p_5x5[2][4] \
          + (4/256)*p_5x5[3][0] + (16/256)*p_5x5[3][1] + (24/256)*p_5x5[3][2] + (16/256)*p_5x5[3][3] + (4/256)*p_5x5[3][4] \
          + (1/256)*p_5x5[4][0] + (4/256)*p_5x5[4][1] + (6/256)*p_5x5[4][2] + (4/256)*p_5x5[4][3] + (1/256)*p_5x5[4][4])
    return int(clip(fp))

微分フィルタ

エッジ検出（ハイパス）

１次微分。x軸方向

\( A_{x}=\frac{\partial{A}}{\partial{x}} \)

0	0	0
0	-1	1
0	0	0

0	0	0
-1	1	0
0	0	0

0	0	0
\( -\frac{1}{2} \)	0	\( \frac{1}{2} \)
0	0	0

y軸方向

\( A_{y}=\frac{\partial{A}}{\partial{y}} \)

0	1	0
0	-1	0
0	0	0

0	0	0
0	1	0
0	-1	0

0	\( \frac{1}{2} \)	0
0	0	0
0	\( -\frac{1}{2} \)	0

勾配の大きさ\[ \sqrt{A_{x}^{2}+A_{y}^{2}} \]

ソーベルフィルタ(Sobel operator)

平滑化（重み付き）と微分の組み合わせ

\( \frac{\partial{A}}{\partial{x}} \)
-1	0	1
-2	0	2
-1	0	1

\( \frac{\partial{A}}{\partial{y}} \)
1	2	1
0	0	0
-1	-2	-1

２次微分フィルタ

変化のピークは0交差

\( \frac{\partial^2{A}}{\partial{x^2}} \)
0	0	0
1	-2	1
0	0	0

\( \frac{\partial^2{A}}{\partial{y^2}} \)
0	1	0
0	-2	0
0	1	0

ラプラシアンフィルタ

２次微分の横方向と縦方向を合わせたもの

0	1	0
1	-4	1
0	1	0

LoGフィルタ(Laplacian of Gaussian)

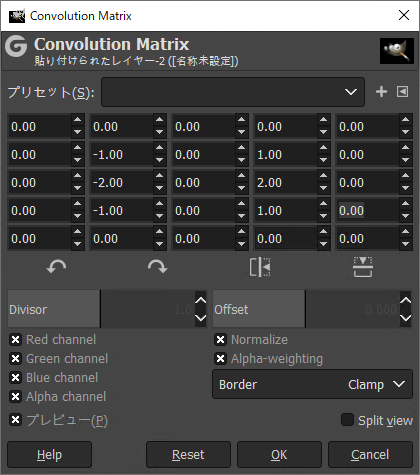
平滑化と２次微分の組み合わせ

GIMPを使ってフィルタリング

「Filters」メニュー → 「Generic」 → 「Convolution Matrix...」

周波数フィルタリング

２次元FFTについて《積み残し》

キャニーのエッジ検出(Canny edge detector)

《積み残し》

ハフ変換(Hough transformation)

直線の検出について《積み残し》

ハリスのコーナー検出器

《積み残し》

SIFT, SURF

《積み残し》

DoGフィルタ

《積み残し》

テンプレートマッチング

差の絶対値の和(Sum of Absolute Differences)

\[ R_{SAD}=\sum_{j=1}^{N}\sum_{i=1}^{M}|I(i,j)-T(i,j)| \]

C/C++ Python

C/C++	Python
`#include <stdint.h> #include <cstdlib> static int sad(const uint8_t block1, const uint8_t block2, int count) { int sum = 0; for (int i = 0; i < count; i++) (sum += std::abs((int)(block1[i]) - (int)(block2[i]))); return sum; }`	`def sad(I, T): retval = 0 for i in range(0, 2): for j in range(0, 2): retval += abs(I[i][j] - T[i][j]) return retval`

#include <stdint.h>
#include <cstdlib>

static int sad(const uint8_t *block1, const uint8_t *block2, int count) {
        int sum = 0;
        for (int i = 0; i < count; i++) (sum += std::abs((int)(block1[i]) - (int)(block2[i])));
        return sum;
}

def sad(I, T):
    retval = 0
    for i in range(0, 2):
        for j in range(0, 2):
            retval += abs(I[i][j] - T[i][j])
    return retval

二乗和誤差の和(Sum of Squared Differences)

\[ R_{SSD}=\sum_{j=1}^{N}\sum_{i=1}^{M}(I(i,j)-T(i,j))^2 \]

Python
`def ssd(I, T): retval = 0 for i in range(0, 2): for j in range(0, 2): retval += (I[i][j] - T[i][j])**2 return retval`

正規化相関(Normalized Cross-Correlation)

\[ R_{NCC}=\frac{\sum_{j=1}^{N}\sum_{i=1}^{M}I(i,j)T(i,j)}{\sqrt{\sum_{j=1}^{N}\sum_{i=1}^{M}I(i,j)^{2}\sum_{j=1}^{N}\sum_{i=1}^{M}T(i,j)^{2}}} \]

import math

def ncc(I, T):
    a, b, c = 0, 0, 0
    for i in range(0, 2):
        for j in range(0, 2):
            a += I[i][j]*T[i][j]
            b += (I[i][j])**2
            c += (T[i][j])**2
    return a / math.sqrt(b*c)

内積をとってそれぞれのノルムで割っている（cos θを見ている）

ZSAD, ZSSD, ZNCC

画像の明るさが（数値として見ると大きく）影響するので、画像のウインドウ内の平均が０になるように正規化（平均で引く）する(Zero-mean)

ステレオマッチング

線上を探索。同じところは同じように（同じ色に）見えているはず

同じところだと判断できるのは模様のある（画素の値が変化している）ところだけ

もともとの領域とは関係のない小領域を作るので、エッジが鈍る

各画素について、対応する画素はたかだか１つ(up to 1)存在する（一意性）

画像と空間の関係を記述

カメラ座標系と世界座標系の関係は剛体変換（座標変換）で表現
３次元を２次元にピンホールカメラモデルで投影

立方体を投影

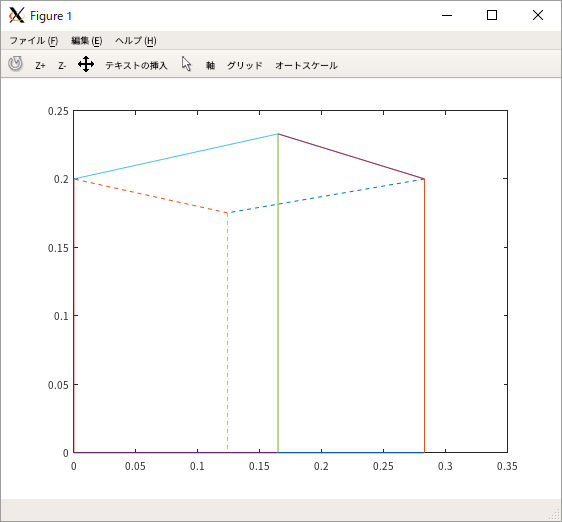
（陰線処理はハードコーディングによる）

ソースコード

カメラの内部パラメタ(intrinsic parameter)

(x, y)が何ピクセル目に映っているかは、ピクセルの大きさΔdで割る。（デジタル化）\[ x'=x/\Delta d+O_x \\ y'=y/\Delta d+O_y \]（x', y'：何ピクセル目か）

(O_x, O_y)を足す。画像座標系は左上が原点（カメラ座標系は投影中心が原点）

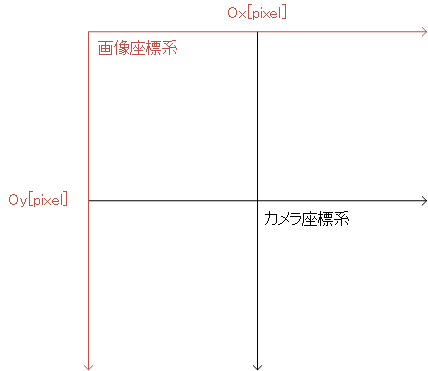
単位は、(x', y')は[pixel]。(x, y)は[m]、Δdは[m/pixel]、(O_x, O_y)は[pixel]

S_x, S_y：ピクセルの大きさの逆数（x方向とy方向で微妙に画素の大きさが違うことがあるので分けている）\[ \left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)=\left( \begin{array}{ccc} S_x & S_\theta & O_x \\ 0 & S_y & O_y \\ 0 & 0 & 1 \end{array} \right)\left( \begin{array}{c} x \\ y \\ 1 \end{array} \right) \]

S_θは（０でもよいが）小さい数。（加工の精度の問題による）画像面の傾きを補正（ノウハウ的）

ピンホールカメラモデル。（カメラ座標系で）４次元のベクトル(X Y Z 1)^Tを(x y 1)^Tに変換する\[ \left( \begin{array}{c} x \\ y \\ 1 \end{array} \right)=\frac{1}{Z}\left( \begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right)\left( \begin{array}{c} X \\ Y \\ Z \\ 1 \end{array} \right) \]

カメラの内部パラメタ（積にしたものが使われる）\[ \left( \begin{array}{ccc} S_x & S_\theta & O_x \\ 0 & S_y & O_y \\ 0 & 0 & 1 \end{array} \right)\left( \begin{array}{cccc} f & 0 & 0 & 0 \\ 0 & f & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array} \right)=\left( \begin{array}{cccc} S_{x}f & S_\theta & O_x & 0 \\ 0 & S_{y}f & O_y & 0 \\ 0 & 0 & 1 & 0 \end{array} \right) \]（よくKと書かれる）\[ K=\left( \begin{array}{ccc} S_{x}f & S_\theta & O_x \\ 0 & S_{y}f & O_y \\ 0 & 0 & 1 \end{array} \right) \]

S_xf, S_yf：画素の大きさの逆数と焦点距離の積にしか意味がない（分離できない）

λはスケールファクターと呼ばれる\[ \left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)=\frac{1}{Z}\left( \begin{array}{cccc} S_{x}f & S_\theta & O_x & 0 \\ 0 & S_{y}f & O_y & 0 \\ 0 & 0 & 1 & 0 \end{array} \right)\left( \begin{array}{c} X \\ Y \\ Z \\ 1 \end{array} \right) \]左辺は画像座標系で右辺はカメラ座標系なので、形式的にZは（紛らわしいので）使わない\[ \lambda\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)=\left( \begin{array}{cccc} S_{x}f & S_\theta & O_x & 0 \\ 0 & S_{y}f & O_y & 0 \\ 0 & 0 & 1 & 0 \end{array} \right)\left( \begin{array}{c} X \\ Y \\ Z \\ 1 \end{array} \right) \]

レンズ歪

半径方向歪（や円周方向歪）について《積み残し》

カメラ外部パラメタ(extrinsic parameter)

剛体変換\[ \left( \begin{array}{c} X \\ Y \\ Z \\ 1 \end{array} \right)=\left( \begin{array}{cccc} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \\ 0 & 0 & 0 & 1 \end{array} \right)\left( \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right) \]

射影変換行列

カメラの内部パラメタと外部パラメタを、線形変換で重ねる\[ \lambda\left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)=\left( \begin{array}{cccc} S_{x}f & S_\theta & O_x & 0 \\ 0 & S_{y}f & O_y & 0 \\ 0 & 0 & 1 & 0 \end{array} \right)\left( \begin{array}{cccc} R_{11} & R_{12} & R_{13} & t_x \\ R_{21} & R_{22} & R_{23} & t_y \\ R_{31} & R_{32} & R_{33} & t_z \\ 0 & 0 & 0 & 1 \end{array} \right)\left( \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right)=\left( \begin{array}{cccc} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & p_{34} \end{array} \right)\left( \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right) \]

世界座標系で表されたX_W, Y_W, Z_Wが画像の何ピクセル目に映るかが分かる

カメラキャリブレーション

射影変換行列を求める

Direct Linear Transform(DLT)法

３次元座標が既知の点が画像のどのピクセルに投影されるかを（たくさん）みることによって、射影変換行列を求める

定数倍の不定性をさけるために射影変換行列の右下(p₃₂成分)を１とする\[ \left( \begin{array}{c} x' \\ y' \\ 1 \end{array} \right)\sim\left( \begin{array}{cccc} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & 1 \end{array} \right)\left( \begin{array}{c} X_W \\ Y_W \\ Z_W \\ 1 \end{array} \right) \]（λが掛かっているが、定数倍は等しいとして求める）

（見やすいように、）世界座標系の__Wを省略して、x'をu、y'をvと書き直す\[ \left( \begin{array}{c} u \\ v \\ 1 \end{array} \right)\sim\left( \begin{array}{cccc} p_{11} & p_{12} & p_{13} & p_{14} \\ p_{21} & p_{22} & p_{23} & p_{24} \\ p_{31} & p_{32} & p_{33} & 1 \end{array} \right)\left( \begin{array}{c} X \\ Y \\ Z \\ 1 \end{array} \right) \]

ひとつひとつの式を書き下す\[ u_{i}=\frac{p_{11}X_{i}+p_{12}Y_{i}+p_{13}Z_{i}+p_{14}}{p_{31}X_{i}+p_{32}Y_{i}+p_{33}Z_{i}+1} \]\[ v_{i}=\frac{p_{21}X_{i}+p_{22}Y_{i}+p_{23}Z_{i}+p_{24}}{p_{31}X_{i}+p_{32}Y_{i}+p_{33}Z_{i}+1} \]

射影変換行列には11個未知数がある。既知の点が１つあると方程式が２本立てられるので、６点以上あれば射影変換行列が求められる

（最小二乗法で解く）

p₁₁～p₃₃が未知数なので、式をまとめる\[ p_{11}X_{i}+p_{12}Y_{i}+p_{13}Z_{i}+p_{14}-p_{31}X_{i}u_{i}-p_{32}Y_{i}u_{i}-p_{33}Z_{i}u_{i}=u_{i} \]\[ p_{21}X_{i}+p_{22}Y_{i}+p_{23}Z_{i}+p_{24}-p_{31}X_{i}v_{i}-p_{32}Y_{i}v_{i}-p_{33}Z_{i}v_{i}=v_{i}\]

（分数になっているが、pに関しては線形な式）\[ \left( \begin{array}{ccccccccccc} X_i & Y_i & Z_i & 1 & 0 & 0 & 0 & 0 & -X_{i}u_{i} & -Y_{i}u_{i} & -Z_{i}u_{i} \\ 0 & 0 & 0 & 0 & X_{i} & Y_i & Z_i & 1 & -X_{i}v_{i} & -Y_{i}v_{i} & -Z_{i}v_{i} \end{array} \right)\left( \begin{array}{c} p_{11} \\ p_{12} \\ p_{13} \\ p_{14} \\ p_{21} \\ p_{22} \\ p_{23} \\ p_{24} \\ p_{31} \\ p_{32} \\ p_{33} \end{array} \right)=\left( \begin{array}{c} u_i \\ v_i \end{array} \right) \]

6点以上あれば、pの各成分が\[ A\mathbf{p}=\mathbf{b}\\\mathbf{p}=(A^{T}A)^{-1}A^{T}\mathbf{b}\]として求まる。(A^TA)^-1A^Tは一般化逆行列（疑似逆行列）

（２個カメラがあったらそれぞれ同じことをやる）

３次元座標の計算

ステレオカメラのp_kは既知、３次元座標X, Y, Zが未知（DLTと同じ式で求めるものが違う）\[ u_{k}=\frac{{p_{k}}_{11}X+{p_{k}}_{12}Y+{p_{k}}_{13}Z+{p_{k}}_{14}}{{p_{k}}_{31}X+{p_{k}}_{32}Y+{p_{k}}_{33}Z+1} \]\[ v_{k}=\frac{{p_{k}}_{21}X+{p_{k}}_{22}Y+{p_{k}}_{23}Z+{p_{k}}_{24}}{{p_{k}}_{31}X+{p_{k}}_{32}Y+{p_{k}}_{33}Z+1} \]

X, Y, Zに対して線形にかかっている\[ ({p_{k}}_{11}-u_{k}{p_{k}}_{31})X+({p_{k}}_{12}-u_{k}{p_{k}}_{32})Y+({p_{k}}_{13}-u_{k}{p_{k}}_{33})Z=u_{k}-{p_{k}}_{14} \]\[ ({p_{k}}_{21}-v_{k}{p_{k}}_{31})X+({p_{k}}_{22}-v_{k}{p_{k}}_{32})Y+({p_{k}}_{23}-v_{k}{p_{k}}_{33})Z=v_{k}-{p_{k}}_{24} \]

３つ未知数があり、ステレオカメラで見ると（k=1とk=2の場合があるので）方程式は４本立てられる\[ \left( \begin{array}{ccc} {p_{1}}_{11}-u_{1}{p_{1}}_{31} & {p_{1}}_{12}-u_{1}{p_{1}}_{32} & {p_{1}}_{13}-u_{1}{p_{1}}_{33} \\ {p_{1}}_{21}-v_{1}{p_{1}}_{31} & {p_{1}}_{22}-v_{1}{p_{1}}_{32} & {p_{1}}_{23}-v_{1}{p_{1}}_{33} \\ {p_{2}}_{11}-u_{2}{p_{2}}_{31} & {p_{2}}_{12}-u_{2}{p_{2}}_{32} & {p_{2}}_{13}-u_{2}{p_{2}}_{33} \\ {p_{2}}_{21}-v_{2}{p_{2}}_{31} & {p_{2}}_{22}-v_{2}{p_{2}}_{32} & {p_{2}}_{23}-v_{2}{p_{2}}_{33} \end{array} \right)\left( \begin{array}{c} X \\ Y \\ Z \end{array} \right)=\left( \begin{array}{c} u_{1}-{p_{1}}_{14} \\ v_{1}-{p_{1}}_{24} \\ u_{2}-{p_{2}}_{14} \\ v_{2}-{p_{2}}_{24} \end{array} \right) \]

線形最小二乗法で求める\[ p\mathbf{x}=\mathbf{q} \\ \mathbf{x}=(p^{T}p)^{-1}p^{T}\mathbf{q}=q^{\dagger}\mathbf{q} \]

pは正方行列でないので逆行列p^-1は求められない。p^†はpの一般化逆行列（疑似逆行列）。数値計算で求める

octave:1> p = [1 2 3; 4 5 6; 7 8 9; 10 11 12]
p =

    1    2    3
    4    5    6
    7    8    9
   10   11   12

octave:2> pinv(p)
ans =

  -0.4833333  -0.2444444  -0.0055556   0.2333333
  -0.0333333  -0.0111111   0.0111111   0.0333333
   0.4166667   0.2222222   0.0277778  -0.1666667

エピポーラ幾何

ベクトルの内積と外積

内積\[ \left( \begin{array}{c} a \\ b \\ c \end{array} \right) \cdot \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} a \\ b \\ c \end{array} \right)^\mathrm{T} \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{ccc} a & b & c \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = ax + by + cz \]

内積の性質\[ \left( \begin{array}{c} a \\ b \\ c \end{array} \right) \perp \left( \begin{array}{c} x \\ y \\ z \end{array} \right) なら0 \]

外積\[ \left( \begin{array}{c} a \\ b \\ c \end{array} \right) \times \left( \begin{array}{c} x \\ y \\ z \end{array} \right) = \left( \begin{array}{c} bz-cy \\ cx-az \\ ay-bx \end{array} \right) = \left( \begin{array}{ccc} 0 & -c & b \\ c & 0 & -a \\ -b & a & 0 \end{array} \right) \left( \begin{array}{c} x \\ y \\ z \end{array} \right) \]

外積の性質\[ \left( \begin{array}{c} a \\ b \\ c \end{array} \right) \parallel \left( \begin{array}{c} x \\ y \\ z \end{array} \right) なら0 \]

基本行列(Essential matrix)

（２つのカメラの）ピンホールカメラモデル。カメラ１、２のカメラ座標系での物体の点\[ \mathbf{X}_{1}=\lambda_{1}\left( \begin{array}{c} x_1 \\ y_1 \\ f \end{array} \right), \mathbf{X}_{2}=\lambda_{2}\left(\begin{array}{c} x_{2} \\ y_{2} \\ f \end{array}\right) \]

（２つのカメラ間の）剛体変換\[ \mathbf{X}_{2} = R\mathbf{X}_{1}+\mathbf{t} \]

Essential matrixの導出

\[ \lambda_{2}\mathbf{x}_{2}=\lambda_{1}R\mathbf{x}_{1}+\mathbf{t} \]	（奥行きλを消去したい）
\[ \lambda_{2}\mathbf{t}\times\mathbf{x}_{2}=\lambda_{1}\mathbf{t}\times R\mathbf{x}_{1}+\mathbf{t}\times\mathbf{t} \]	辺々にt×
\[ \lambda_{2}\mathbf{t}\times\mathbf{x}_{2}=\lambda_{1}\mathbf{t}\times R\mathbf{x}_{1} \]	t×tは0
\[ \lambda_{2}\mathbf{x}_{2}\cdot\mathbf{t}\times\mathbf{x}_{2}=\lambda_{1}\mathbf{x}_{2}\cdot\mathbf{t}\times R\mathbf{x}_{1} \]	辺々にx₂⋅
\[ 0=\lambda_{1}\mathbf{x}_{2}\cdot\mathbf{t}\times R\mathbf{x}_{1} \]	x₂⋅t×x₂は0
\[ \mathbf{x}_{2}\cdot\mathbf{t}\times R\mathbf{x}_{1}=0 \]	λ₁を消去
\[ x_{2}^{T}\mathbf{t}\times R\mathbf{x}_{1}=0 \]	内積を行列の積で書く
\[ x_{2}^{T}\hat{T}Rx_{1}=0 \]	外積を行列の積で書く
\[ x_{2}^{T}Ex_{1}=0 \]	\( \hat{T}R \)をE行列と置く（欲しかった式を得る）

\( \hat{T} \)はベクトルの外積より\[ \hat{T}=\left( \begin{array}{ccc} 0 & -t_z & t_y \\ t_z & 0 & -t_x \\ -t_y & t_x & 0 \end{array} \right) \]

エピポーラ線

\[ \left( \begin{array}{ccc} a & b & 1 \end{array} \right)\left( \begin{array}{ccc} e_{11} & e_{12} & e_{13} \\ e_{21} & e_{22} & e_{23} \\ e_{31} & e_{32} & e_{33} \end{array} \right)\left( \begin{array}{c} x_2 \\ y_2 \\ 1 \end{array} \right)=0 \]\[ \left( \begin{array}{ccc} ae_{11}+be_{21}+e_{31} & ae_{12}+be_{22}+e_{32} & ae_{13}+be_{23}+e_{33} \end{array}\right)\left( \begin{array}{c} x_2 \\ y_2 \\ 1 \end{array} \right)=0 \]\[ (ae_{11}+be_{21}+e_{31})x_{2}+(ae_{12}+be_{22}+e_{32})y_{2}+ae_{13}+be_{23}+e_{33}=0 \]\[ y_{2}=-\frac{ae_{11}+be_{21}+e_{31}}{ae_{12}+be_{22}+e_{32}}x_{2}-\frac{ae_{13}+be_{23}+e_{33}}{ae_{12}+be_{22}+e_{32}} \]

基礎行列(Fundamental matrix)

F行列について《積み残し》

平行ステレオカメラの平行化

rectificationについて《積み残し》

ホモグラフィ

（OpenCVのチュートリアル）

#!/usr/bin/env python3

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.cvtColor(cv2.imread('DSCF1216.JPG'), cv2.COLOR_RGB2BGR)

a = [1320,1260]
b = [2380,1267]
c = [2271,673]
d = [1383,666]

pts1 = np.float32([a, b, c, d])

center = [(a[0]+b[0]+c[0]+d[0])/4, (a[1]+b[1]+c[1]+d[1])/4]
half_size =  ((b[0]+c[0])/2 - (a[0]+d[0])/2)/2

pts2 = np.float32([[center[0] - half_size, center[1] + half_size],
                   [center[0] + half_size, center[1] + half_size],
                   [center[0] + half_size, center[1] - half_size],
                   [center[0] - half_size, center[1] - half_size]])

H = cv2.getPerspectiveTransform(pts1, pts2)
dst = cv2.warpPerspective(img, H, (3584, 2016))

plt.subplot(211), plt.imshow(img), plt.title('original')
plt.subplot(212), plt.imshow(dst), plt.title('bird view')
plt.show()
#plt.savefig('fig7.jpg')

pts1は目視、手作業で決定。pts2は適当に決定

OpenCVが求めたH（射影変換行列）

In [2]: H
Out[2]:
array([[  1.37760936e+00,   7.05209153e-01,  -6.62795412e+02],
       [ -2.24030170e-02,   2.67616320e+00,  -1.14390099e+03],
       [ -5.98209065e-06,   4.13053342e-04,   1.00000000e+00]])

視差(disparity)マップの作成

.MPOファイルから左右の画像を取り出す（備忘録）

$ exiftool -trailer:all= DSCF1216.MPO -o DSCF1216_L.JPG
    1 image files created
$ exiftool DSCF1216.MPO -mpimage2 -b > DSCF1216_R.JPG

（左右は、撮影者側から見て、左カメラ、右カメラ）

（OpenCVのチュートリアル）

#!/usr/bin/env python3

import cv2
import numpy as np
import matplotlib.pyplot as plt
import sys

imgL = cv2.cvtColor(cv2.imread(sys.argv[1]), cv2.COLOR_RGB2GRAY)
imgR = cv2.cvtColor(cv2.imread(sys.argv[2]), cv2.COLOR_RGB2GRAY)

stereo = cv2.StereoBM_create(numDisparities=64, blockSize=21)
disparity = stereo.compute(imgL, imgR)

plt.subplot(221), plt.imshow(imgL, 'gray'), plt.title('left camera')
plt.subplot(222), plt.imshow(imgR, 'gray'), plt.title('right camera')
plt.subplot(223), plt.imshow(disparity, 'gray'), plt.title('disparity map')
plt.show()
#plt.savefig('fig8.jpg')

baseline length = 75mm

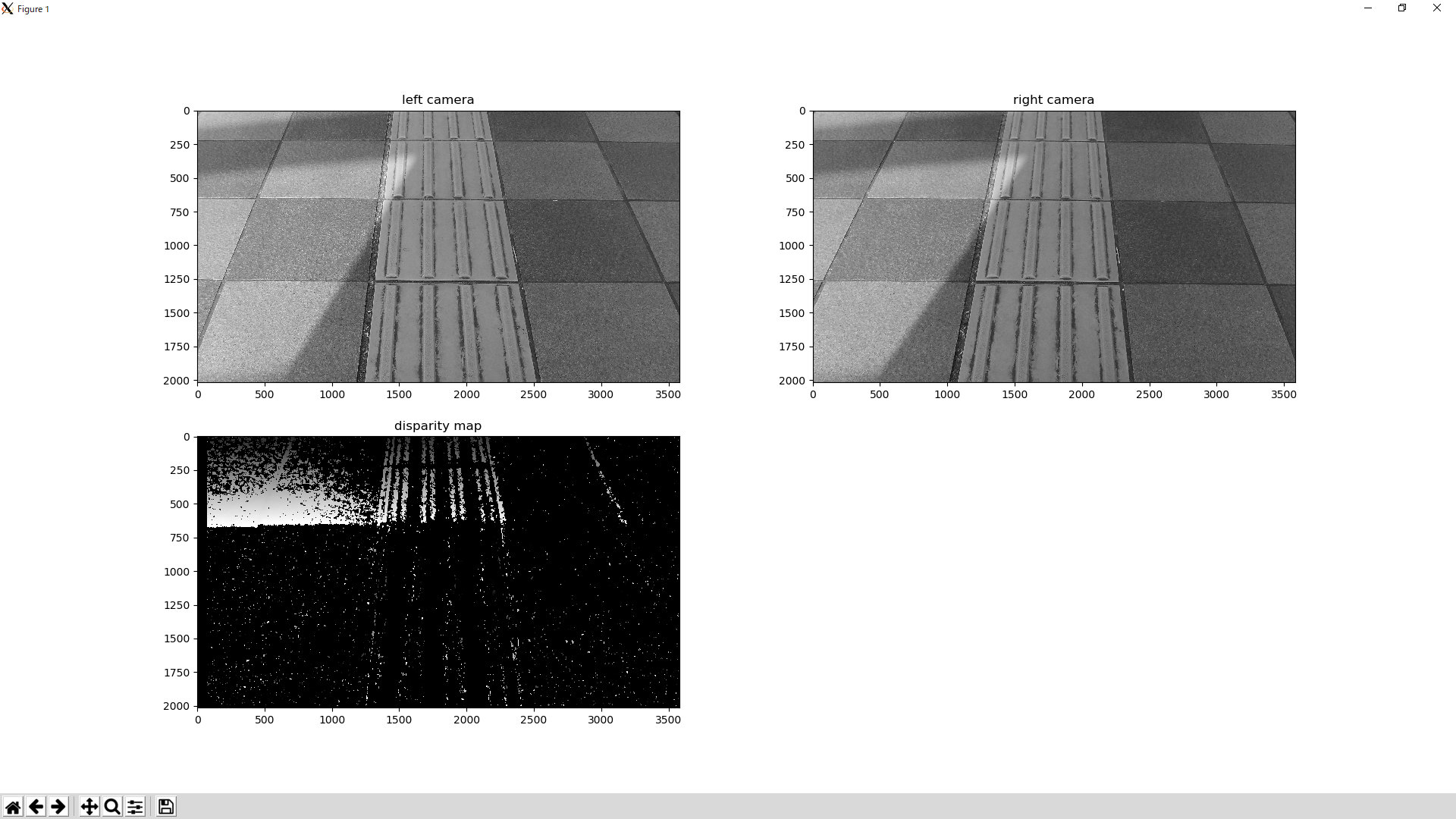
baseline length = 不明

差分画像(subtraction image)

背景差分(background subtraction method)、フレーム間差分(frame subtraction method)について《積み残し》

オプティカルフロー

《積み残し》

解像度を落とす(Gaussian pyramid)

粗密探索(Coarse-to-fine)アプローチについて《積み残し》

コンピュータビジョン

ピンホールカメラモデル(Pinhole camera model)

平行ステレオ

カメラ座標系と世界座標系の関係

クォータニオン(Quaternion)

四元数(Quaternion)による回転の例

OctaveのQuaternionパッケージ

OctaveとWolfram言語でQuaternion

空間フィルタリング

加重平均フィルタ

微分フィルタ

ソーベルフィルタ(Sobel operator)

２次微分フィルタ

ラプラシアンフィルタ

LoGフィルタ(Laplacian of Gaussian)

GIMPを使ってフィルタリング

周波数フィルタリング

キャニーのエッジ検出(Canny edge detector)

ハフ変換(Hough transformation)

ハリスのコーナー検出器

SIFT, SURF

DoGフィルタ

テンプレートマッチング

差の絶対値の和(Sum of Absolute Differences)

二乗和誤差の和(Sum of Squared Differences)

正規化相関(Normalized Cross-Correlation)

ZSAD, ZSSD, ZNCC

ステレオマッチング

画像と空間の関係を記述

カメラの内部パラメタ(intrinsic parameter)

レンズ歪

カメラ外部パラメタ(extrinsic parameter)

射影変換行列

カメラキャリブレーション

Direct Linear Transform(DLT)法

３次元座標の計算

エピポーラ幾何

基本行列(Essential matrix)

エピポーラ線

基礎行列(Fundamental matrix)

平行ステレオカメラの平行化

ホモグラフィ

視差(disparity)マップの作成

差分画像(subtraction image)

オプティカルフロー

解像度を落とす(Gaussian pyramid)