ディジタル制御
永井 忠一 2023.9.9
離散時間システム
離散化のイメージ
T は制御周期、もしくはサンプリング周期(Ts と書かれることもある)
(* 同じ文字で書かれることがある時定数の T とは別のものなので、混同しないように注意)
(* 実際には、制御周期 T は可能な限り十分に小さくする)
上記の、作図プログラム
| Octave |
|---|
$ octave --no-gui
GNU Octave, version 6.4.0
Copyright (C) 2021 The Octave Project Developers.
This is free software; see the source code for copying conditions.
There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE. For details, type 'warranty'.
Octave was configured for "x86_64-pc-linux-gnu".
Additional information about Octave is available at https://www.octave.org.
Please contribute if you find this software useful.
For more information, visit https://www.octave.org/get-involved.html
Read https://www.octave.org/bugs.html to learn how to submit bug reports.
For information about changes from previous versions, type 'news'.
octave:1> type -q sampling.m
x = linspace(0, 2*pi, 1024);
y = (sin(x - 0.5*pi) + 1)/2;
clf
plot(x, y)
T = 1.0; % [s]
x_d = 0:T:x(length(x));
y_d = (sin(x_d - 0.5*pi) + 1)/2;
hold on
stem(x_d, y_d)
legend("continuous time system", "discrete time system")
title("discretization; T = 1.0")
xlabel("time [s]")
print("fig_sampling.svg", "-dsvg")
octave:2> sampling
|
ゼロ次ホールド
(0次ホールド、零次ホールドとも書かれる)
作図プログラム
| Octave |
|---|
octave:1> type -q zero_order_hold.m
x = linspace(0, 2*pi, 1024);
y = (sin(x - 0.5*pi) + 1)/2;
clf
plot(x, y)
T = 1.0; % [s]
x_d = 0:T:x(length(x));
y_d = (sin(x_d - 0.5*pi) + 1)/2;
hold on
stem(x_d, y_d, ls=":")
x = []; y = [];
for i = 1:length(x_d)
if i != 1
x = [x, NaN];
y = [y, NaN];
end
x = [x, x_d(i), x_d(i) + T];
y = [y, y_d(i), y_d(i)];
end
plot(x, y)
legend("continuous time system", "discrete time system", "zero-order hold")
title("discretization; T = 1.0")
xlabel("time [s]")
print("fig_zero-order_hold.svg", "-dsvg")
octave:2> zero_order_hold
|
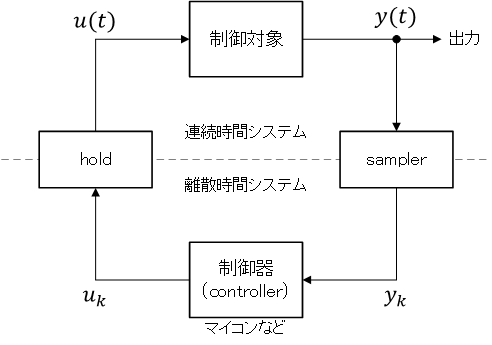
サンプラとホールド
ディジタル制御システムの構成
古典制御理論(周波数領域)
《以下、積み残し》
- z 変換
- 双一次変換(Tustin 変換、双一次 z 変換とも)
(以下は、現代制御理論(時間領域))
状態方程式の解
(連続時間システムの)状態方程式 \( \dot{\boldsymbol x}(t) = A\boldsymbol{x}(t) + B\boldsymbol{u}(t) \) の解(式 再掲)\[ \boldsymbol x(t) = e^{A(t - t_0)}\boldsymbol x(t_0) + \int_{t_0}^{t}e^{A(t - \tau)}B\boldsymbol u(\tau)\, d\tau \]
制御周期 \( T \) を一定として、ゼロ次ホールド法(入力 \( \boldsymbol u(t) \) は制御周期内で一定とする )で状態方程式の解を離散化する\[ \begin{align}
\boldsymbol x(t + T) &= e^{A(t + T - t_0)}\boldsymbol x(t_0) + \int_{t_0}^{t + T}e^{A(t + T - \tau)}B\boldsymbol u(t)\, d\tau \\
&= e^{A(t + T - t_0)}\boldsymbol x(t_0) + e^{A(t + T)}\int_{t_0}^{t + T}e^{-A\tau}B\boldsymbol u(t)\, d\tau \\
&= e^{A(t + T - t_0)}\boldsymbol x(t_0) + e^{A(t + T)}\int_{t_0}^{t}e^{-A\tau}B\boldsymbol u(t)\, d\tau + e^{A(t + T)}\int_{t}^{t + T}e^{-A\tau}B\boldsymbol u(t)\, d\tau \\
&= e^{AT}\left\{e^{A(t - t_0)}\boldsymbol x(t_0) + e^{At}\int_{t_0}^{t}e^{-A\tau}B\boldsymbol u(t)\, d\tau\right\} + e^{A(t + T)}\int_{t}^{t + T}e^{-A\tau}B\boldsymbol u(t)\, d\tau \\
&= e^{AT}\left\{e^{A(t - t_0)}\boldsymbol x(t_0) + \int_{t_0}^{t}e^{A(t - \tau)}B\boldsymbol u(t)\, d\tau\right\} + e^{A(t + T)}\int_{t}^{t + T}e^{-A\tau}B\boldsymbol u(t)\, d\tau \\
&= e^{AT}\boldsymbol x(t) + e^{A(t + T)}\int_{t}^{t + T}e^{-A\tau}B\boldsymbol u(t)\, d\tau \\
&= e^{AT}\boldsymbol x(t) + e^{A(t + T)}\left(\int_{t}^{t + T}e^{-A\tau}\, d\tau\right)B\boldsymbol u(t)
\end{align} \]
右辺第2項の積分\[ \boldsymbol x(t + T) = e^{AT}\boldsymbol x(t) + \boxed{e^{A(t + T)}\int_{t}^{t + T}e^{-A\tau}\, d\tau}B\boldsymbol u(t) \]を、\( \boxed{ \tau^\prime = \tau - t} \) と変数変換して置換積分\[ \begin{align}
\boldsymbol x(t + T) &= e^{AT}\boldsymbol x(t) + e^{A(t + T)}\left(\int_{t}^{t + T}e^{-A\tau}\, d\tau\right)B\boldsymbol u(t) \\
&= e^{AT}\boldsymbol x(t) + \left(\int_{t}^{t + T}e^{A(t + T)}\cdot e^{-A\tau}\, d\tau\right)B\boldsymbol u(t) \\
&= e^{AT}\boldsymbol x(t) + \left(\int_{0}^{T}e^{AT}\cdot e^{-A\tau^\prime}\, d\tau^\prime\right)B\boldsymbol u(t) \\
&= e^{AT}\boldsymbol x(t) + \left(\int_{0}^{T}e^{A(T - \tau^\prime)}\, d\tau^\prime\right)B\boldsymbol u(t)
\end{align} \]
得られた式の解釈\[ \boldsymbol x(t + T) = \boxed{e^{AT}}\boldsymbol x(t) + \boxed{\left(\int_{0}^{T}e^{A(T - \tau^\prime)}\, d\tau^\prime\right)B}\boldsymbol u(t) \]
∴ 離散時間システムの状態方程式(差分方程式)\[ \boldsymbol x_{k + 1} = A_\mathrm d\boldsymbol x_k + B_\mathrm d\boldsymbol u_k \]ここで \( A_\mathrm d,\, B_\mathrm d \) は\[ A_\mathrm d = e^{AT}, \quad B_\mathrm d = \left(\int_{0}^{T}e^{A(T - \tau^\prime)}\, d\tau^\prime\right)B \](\( A_\mathrm d,\, B_\mathrm d \) の d は、discrete の意味)
(教科書などによっては、差分方程式は添え字をプログラムのようにして\[ \boldsymbol x[k + 1] = A_\mathrm d\boldsymbol x[k] + B_\mathrm d\boldsymbol u[k] \]と書かれることもある)
(また、\( C_\mathrm d = C,\, D_\mathrm d = D \) となる)
置換積分(復習)
上記の計算\[ \int_{t}^{t + T}e^{A(t + T)}\cdot e^{-A\tau}\, d\tau = \int_{0}^{T}e^{A(T - \tau^\prime)}\, d\tau^\prime \]の検算。Maxima の changevar() 関数を利用して確認
| Maxima |
|---|
$ maxima
Maxima 5.47.0 https://maxima.sourceforge.io
using Lisp CLISP 2.49+ (2010-07-17)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
The function bug_report() provides bug reporting information.
(%i1) 'integrate(e^(A*(t + T))*e^(-A*\\tau), \\tau, t, t + T);
(%o1)
\[ \int_{t}^{t+T}{e^{A\,\left(t+T\right)-A\,{\it \tau}}\;d{\it \tau}} \]
(%i2) \\tau\' = \\tau - t;
(%o2)
\[ {\it \tau'}={\it \tau}-t \]
(%i3) changevar(%th(2), %th(1), \\tau\', \\tau);
(%o3)
\[ \int_{0}^{T}{e^{A\,T-A\,{\it \tau'}}\;d{\it \tau'}} \]
|
(Maxima で、%th(N) は N 回前の出力を参照)
状態遷移行列
システムへの入力が無い場合(\( \boldsymbol u = 0 \))の、自由系\[ \boldsymbol x_{k+1} = A_\mathrm d\boldsymbol x_k \]を考える。ここで、\( A_\mathrm d \) 行列は、ある時刻 \( k \) から、次の時刻 \( k+1 \) に、状態変数ベクトル \( \boldsymbol x \) を状態遷移(\( \boldsymbol x_k \) → \( \boldsymbol x_{k+1} \) )させる働きをしていることから、状態遷移行列と呼ばれる
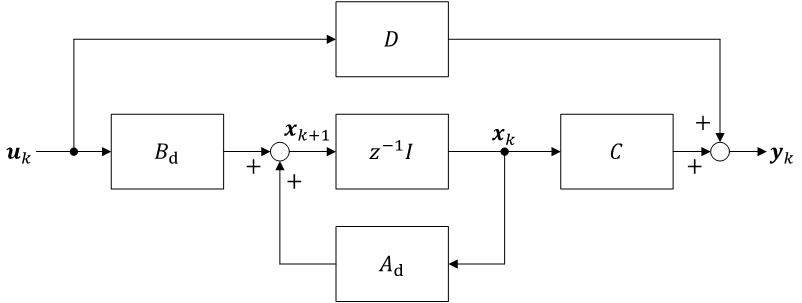
状態変数線図
(cf. 連続時間システムの図)
離散時間システムのブロック線図
\( A_\mathrm d \) 行列と \( B_\mathrm d \) 行列の求め方
Octave の control パッケージや、Scilab などを利用(例には、こちらの連続時間システムを使用)
離散時間システムの \( A_\mathrm d \) 行列と \( B_\mathrm d \) 行列を計算(制御周期 T は、ここでは適当に与えている)
(* また、\( A_\mathrm d \) 行列と \( B_\mathrm d \) 行列は、制御周期 \( T \) によって変わることに注意)
| Octave | Scilab |
|---|
$ octave --no-gui
GNU Octave, version 6.4.0
Copyright (C) 2021 The Octave Project Developers.
This is free software; see the source code for copying conditions.
There is ABSOLUTELY NO WARRANTY; not even for MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE. For details, type 'warranty'.
Octave was configured for "x86_64-pc-linux-gnu".
Additional information about Octave is available at https://www.octave.org.
Please contribute if you find this software useful.
For more information, visit https://www.octave.org/get-involved.html
Read https://www.octave.org/bugs.html to learn how to submit bug reports.
For information about changes from previous versions, type 'news'.
octave:1> pkg load control
octave:2> A = [0 1; -5 -6]
A =
0 1
-5 -6
octave:3> B = [0; 1]
B =
0
1
octave:4> C = [1 0]
C =
1 0
octave:5> D = 0
D = 0
octave:6> T = 0.5 % [s]
T = 0.5000
octave:7> c2d(ss(A, B, C, D), T)
ans.a =
x1 x2
x1 0.7376 0.1311
x2 -0.6556 -0.04903
ans.b =
u1
x1 0.05247
x2 0.1311
ans.c =
x1 x2
y1 1 0
ans.d =
u1
y1 0
Sampling time: 0.5 s
Discrete-time model.
octave:8> A_d = ans.a
A_d =
0.737642 0.131111
-0.655557 -0.049026
octave:9> B_d = ans.b
B_d =
0.052472
0.131111
|
$ scilab -nwni
Scilab branch-6.1 (Apr 14 2022, 22:30:04)
--> A = [0 1; -5 -6]
A =
0. 1.
-5. -6.
--> B = [0; 1]
B =
0.
1.
--> C = [1 0]
C =
1. 0.
--> D = 0
D =
0.
--> T = 0.5 // [s]
T =
0.5
--> dscr(syslin("c", A, B, C, D), T)
ans =
ans(1) (state-space system:)
"lss" "A" "B" "C" "D" "X0" "dt"
ans(2)= A matrix =
0.7376421 0.1311114
-0.6555571 -0.0490264
ans(3)= B matrix =
0.0524716
0.1311114
ans(4)= C matrix =
1. 0.
ans(5)= D matrix =
0.
ans(6)= X0 (initial state) =
0.
0.
ans(7)= Time domain =
0.5
--> [A_d, B_d] = abcd(ans)
A_d =
0.7376421 0.1311114
-0.6555571 -0.0490264
B_d =
0.0524716
0.1311114
|
(\( C_\mathrm d \) 行列と \( D_\mathrm d\) 行列については(式 再掲)\[ C_\mathrm d = C,\quad D_\mathrm d = D \]となる)
可制御性と可観測性
(可到達性、可到達性行列について)《積み残し》
(離散時間システムの)可制御性行列
可制御性行列(cf. 連続時間システムの式)\[ M_\mathrm c = \begin{bmatrix} B_\mathrm d & A_\mathrm d B_\mathrm d & A_\mathrm d^2 B_\mathrm d & \cdots & A_\mathrm d^{n-1} B_\mathrm d \end{bmatrix} \]
可制御性行列 \( M_\mathrm c \) が正則(逆行列を持つ)であれば、可制御である
可制御性行列で可制御性が判定できる理由。離散時間システムの状態方程式(差分方程式)\[ \boldsymbol x_{k+1} = A_\mathrm d\boldsymbol x_k + B_\mathrm d\boldsymbol u_k \]を各タイムステップごとに計算\[ \begin{align}
\boldsymbol x_1 &= A_\mathrm d\boldsymbol x_0 + B_\mathrm d\boldsymbol u_0 \\
\boldsymbol x_2 &= A_\mathrm d\boldsymbol x_1 + B_\mathrm d\boldsymbol u_1 \\
&= A_\mathrm d(A_\mathrm d\boldsymbol x_0 + B_\mathrm d\boldsymbol u_0) + B_\mathrm d\boldsymbol u_1 \\
&= A_\mathrm d^2\boldsymbol x_0 + A_\mathrm d B_\mathrm d\boldsymbol u_0 + B_\mathrm d\boldsymbol u_1 \\
\vdots \\
\boldsymbol x_n &= A_\mathrm d^n\boldsymbol x_0 + A_\mathrm d^{n-1}B_\mathrm d\boldsymbol u_0 + \cdots + B_\mathrm d\boldsymbol u_{n-1}
\end{align} \]
任意の終状態 \( \boldsymbol x_n \) となる入力ベクトルを求めるためには\[ \begin{align}
\boldsymbol x_n &= A_\mathrm d^n\boldsymbol x_0 + A_\mathrm d^{n-1}B_\mathrm d\boldsymbol u_0 + \cdots + B_\mathrm d\boldsymbol u_{n-1} \\
\boldsymbol x_n - A_\mathrm d^n\boldsymbol x_0 &= A_\mathrm d^{n-1}B_\mathrm d\boldsymbol u_0 + \cdots + B_\mathrm d\boldsymbol u_{n-1} \\
\boldsymbol x_n - A_\mathrm d^n\boldsymbol x_0 &= B_\mathrm d\boldsymbol u_{n-1} + \cdots + A_\mathrm d^{n-1}B_\mathrm d\boldsymbol u_0 \\
\boldsymbol x_n - A_\mathrm d^n\boldsymbol x_0 &= \begin{bmatrix} B_\mathrm d & A_\mathrm d B_\mathrm d & A_\mathrm d^2 B_\mathrm d & \cdots & A_\mathrm d^{n-1}B_\mathrm d \end{bmatrix}\begin{pmatrix} \boldsymbol u_{n-1} \\ \boldsymbol u_{n-2} \\ \boldsymbol u_{n-3} \\ \vdots \\ \boldsymbol u_0 \end{pmatrix} \\
\boldsymbol x_n - A_\mathrm d^n\boldsymbol x_0 &= M_\mathrm c\begin{pmatrix} \boldsymbol u_{n-1} \\ \boldsymbol u_{n-2} \\ \boldsymbol u_{n-3} \\ \vdots \\ \boldsymbol u_0 \end{pmatrix} \\
\begin{pmatrix} \boldsymbol u_{n-1} \\ \boldsymbol u_{n-2} \\ \boldsymbol u_{n-3} \\ \vdots \\ \boldsymbol u_0 \end{pmatrix} &= M_\mathrm c^{-1}\left(\boldsymbol x_n - A_\mathrm d^n\boldsymbol x_0\right)
\end{align} \]とするため、システムが可制御であるには、可制御性行列 \( M_\mathrm c \) が正則である(逆行列を持つ)ことが条件となる(必要十分条件)
(離散時間システムの)可観測性行列
可観測性行列(cf. 連測時間システムの式)\[ M_\mathrm{o} = \begin{bmatrix} C \\ C A_\mathrm{d} \\ C A_\mathrm{d}^2 \\ \vdots \\ C A_\mathrm{d}^{n-1} \end{bmatrix} \]
可観測性行列 \( M_\mathrm o \) が正則であれば可観測である理由
離散時間システムの観測方程式(観測方程式は代数方程式)\[ \boldsymbol y_k = C\boldsymbol x_k \](ただし、\( D_\mathrm d = D = 0 \) とする。また、\( C_\mathrm d = C \) である)
観測方程式を各タイムステップごとに計算\[ \begin{align}
\boldsymbol y_0 &= C\boldsymbol x_0 \\
\boldsymbol y_1 &= C\boldsymbol x_1 \\
&= C(A_\mathrm d\boldsymbol x_0 + B_\mathrm d\boldsymbol u_0) \\
\boldsymbol y_2 &= C\boldsymbol x_2 \\
&= C(A_\mathrm d^2\boldsymbol x_0 + A_\mathrm d B_\mathrm d\boldsymbol u_0 + B_\mathrm d\boldsymbol u_1) \\
\vdots
\end{align} \]
行列を使って式を整理\[ \begin{align}
\begin{pmatrix} \boldsymbol y_0 \\ \boldsymbol y_1 \\ \boldsymbol y_2 \\ \vdots \\ \boldsymbol y_{n-1} \end{pmatrix} &= \begin{bmatrix} C \\ C A_\mathrm d \\ C A_\mathrm d^2 \\ \vdots \\ C A_\mathrm d^{n-1} \end{bmatrix}\boldsymbol x_0 + \begin{pmatrix} 0 \\ C B_\mathrm d\boldsymbol u_0 \\ C A_\mathrm d B_\mathrm d\boldsymbol u_0 + C B_\mathrm d\boldsymbol u_1 \\ \vdots \\ C A_\mathrm d^{n-2}B_\mathrm d\boldsymbol u_0 + \cdots + C B_\mathrm d\boldsymbol u_{n-2} \end{pmatrix} \\
\begin{pmatrix} \boldsymbol y_0 \\ \boldsymbol y_1 \\ \boldsymbol y_2 \\ \vdots \\ \boldsymbol y_{n-1} \end{pmatrix} &= M_\mathrm o\boldsymbol x_0 + \begin{pmatrix} 0 \\ C B_\mathrm d\boldsymbol u_0 \\ C A_\mathrm d B_\mathrm d\boldsymbol u_0 + C B_\mathrm d\boldsymbol u_1 \\ \vdots \\ C A_\mathrm d^{n-2}B_\mathrm d\boldsymbol u_0 + \cdots + C B_\mathrm d\boldsymbol u_{n-2} \end{pmatrix}
\end{align} \]
観測された出力から初期状態 \( \boldsymbol x_0 \) を求めるには\[ \begin{align}
\begin{pmatrix} \boldsymbol y_0 \\ \boldsymbol y_1 \\ \boldsymbol y_2 \\ \vdots \\ \boldsymbol y_{n-1} \end{pmatrix} &= M_\mathrm o\boldsymbol x_0 + \begin{pmatrix} 0 \\ C B_\mathrm d\boldsymbol u_0 \\ C A_\mathrm d B_\mathrm d\boldsymbol u_0 + C B_\mathrm d\boldsymbol u_1 \\ \vdots \\ C A_\mathrm d^{n-2}B_\mathrm d\boldsymbol u_0 + \cdots + C B_\mathrm d\boldsymbol u_{n-2} \end{pmatrix} \\
\begin{pmatrix} \boldsymbol y_0 \\ \boldsymbol y_1 \\ \boldsymbol y_2 \\ \vdots \\ \boldsymbol y_{n-1} \end{pmatrix} - \begin{pmatrix} 0 \\ C B_\mathrm d\boldsymbol u_0 \\ C A_\mathrm d B_\mathrm d\boldsymbol u_0 + C B_\mathrm d\boldsymbol u_1 \\ \vdots \\ C A_\mathrm d^{n-2}B_\mathrm d\boldsymbol u_0 + \cdots + C B_\mathrm d\boldsymbol u_{n-2} \end{pmatrix} &= M_\mathrm o\boldsymbol x_0 \\
\boldsymbol x_0 &= M_\mathrm o^{-1}\left\{ \begin{pmatrix} \boldsymbol y_0 \\ \boldsymbol y_1 \\ \boldsymbol y_2 \\ \vdots \\ \boldsymbol y_{n-1} \end{pmatrix} - \begin{pmatrix} 0 \\ C B_\mathrm d\boldsymbol u_0 \\ C A_\mathrm d B_\mathrm d\boldsymbol u_0 + C B_\mathrm d\boldsymbol u_1 \\ \vdots \\ C A_\mathrm d^{n-2}B_\mathrm d\boldsymbol u_0 + \cdots + C B_\mathrm d\boldsymbol u_{n-2} \end{pmatrix} \right\}
\end{align} \]とするため、システムが可観測であるには、可観測性行列 \( M_\mathrm o \) が正則である(逆行列を持つ)ことが条件となる(必要十分条件)
システムの安定性
- 連続時間システムの安定性判別
- \( A \) 行列の固有値(システムの極。一般には複素数)の実部が全て負である(z 平面上で虚軸の左側にある)こと
- 離散時間システムの安定性判別
- \( A_\mathrm d \) 行列の固有値の絶対値が全て 1 より小さい(s 平面上で単位円の内側にある)こと
《詳細は教科書など》
ディジタル再設計
(連続時間で設計した制御器から、(何らかの方法で)離散化をして、離散時間の制御器を得る)
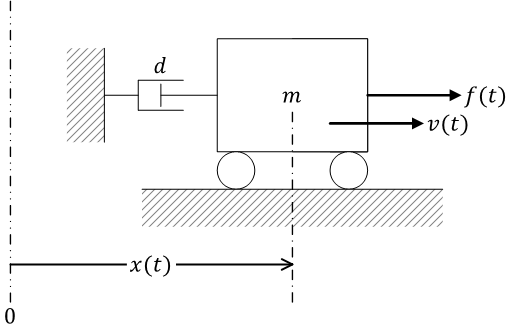
例として考える力学システム。台車モデル
(同じシステムの微分方程式と伝達関数による表現)
システムの状態方程式、状態空間表現(連続時間システム)\[ \left\{ \begin{align}
&\dot{\boldsymbol x}(t) = \begin{bmatrix} 0 & 1 \\ 0 & -d/m \end{bmatrix}\boldsymbol x(t) + \begin{bmatrix} 0 \\ 1/m \end{bmatrix}u(t) \\
&y(t) = \begin{bmatrix} 1 & 0 \end{bmatrix}\boldsymbol x(t)
\end{align} \right. \]
(直達項は \( D = 0 \) として無視)
システムへの入力 \( u(t) \) は力 \( f(t) \)、出力 \( y(t) \) は台車の位置 \( x(t) \)、状態変数ベクトルは \( \begin{pmatrix} x(t) \\ \dot x(t) = v(t) \end{pmatrix} \) としている\[ \left\{ \begin{align}
&\begin{pmatrix} \dot x(t) \\ \ddot x(t) = \dot v(t) \end{pmatrix} = \begin{bmatrix} 0 & 1 \\ 0 & -d/m \end{bmatrix}\begin{pmatrix} x(t) \\ v(t) \end{pmatrix} + \begin{bmatrix} 0 \\ 1/m \end{bmatrix}f(t) \\
&x(t) = \begin{bmatrix} 1 & 0 \end{bmatrix}\begin{pmatrix} x(t) \\ v(t) \end{pmatrix}
\end{align} \right. \]
自由応答
(自由システム。入力が \( u(t) \equiv 0 \))
(システムの零入力応答、あるいは初期値応答とも)
Xcos モデル
| 連続時間システム | 離散時間システム |
|---|
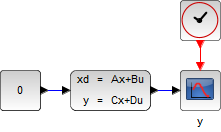 | 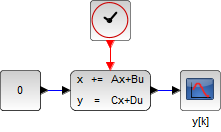 |
Xcos の「コンテキスト設定」
| Xcos |
|---|
// physical parameters
m = 10; // [kg]
d = 2.0; // [N/(m/s)]
// state space representation(continuous time system)
A = [0 1; 0 -d/m];
B = [0; 1/m];
C = [1 0];
D = 0;
// state space representation(discrete time system)
T = 0.001 // sampling period [s]
[Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
// initial state
x = 0; // [m]
v = 1.5; // [m/s]
x0 = [x; v];
|
各「パレット」の設定
| 連続時間システム | 離散時間システム |
|---|
| CLSS | 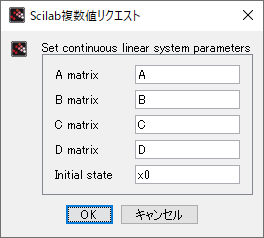 | DLSS | 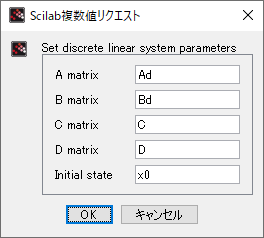 |
|---|
| 連続時間システム | 離散時間システム |
|---|
| CLOCK_c | 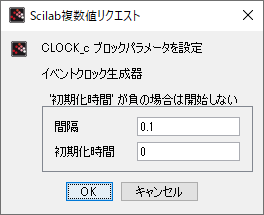 | 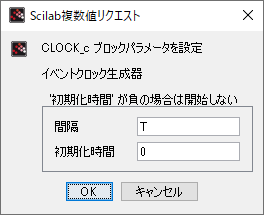 |
|---|
| CSCOPE | 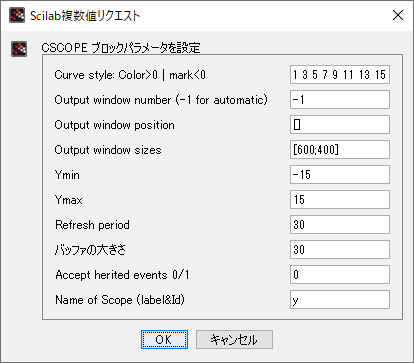 | 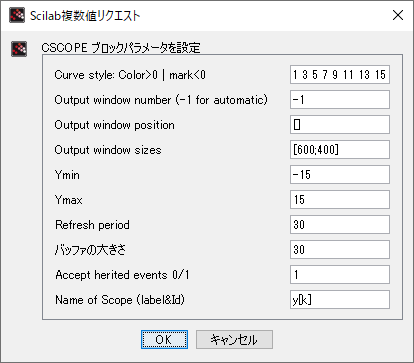 |
|---|
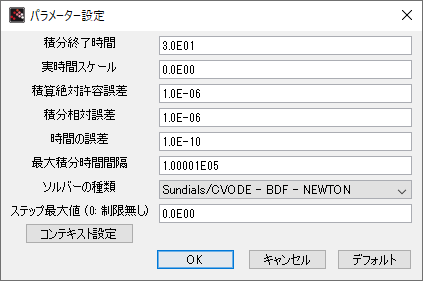
シミュレーションの設定
シミュレーション結果
| 連続時間システム | 離散時間システム |
|---|
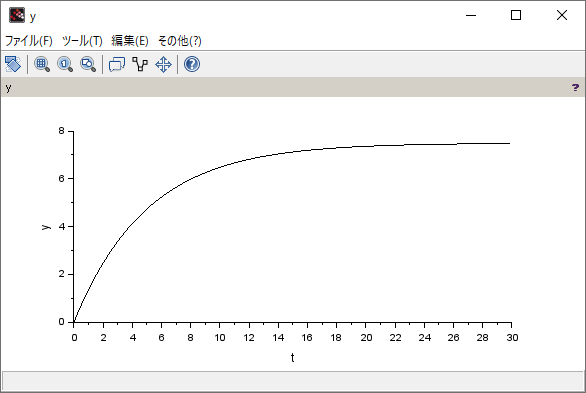 | 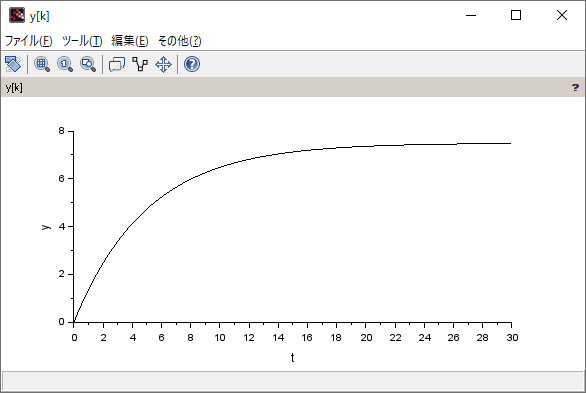 |
(Xcos のプログラム)
システムの安定性、可制御性と可観測性
制御対象の安定性と可制御、可観測性を調べる。プログラムで Uc が可制御性行列、Uo が可観測性行列
| Scilab | Octave |
|---|
--> // physical parameters
--> m = 10; // [kg]
--> d = 2.0; // [N/(m/s)]
--> // state space representation(continuous time system)
--> A = [0 1; 0 -d/m]; B = [0; 1/m];
--> C = [1 0]; D = 0;
--> real(spec(A)) // stability
ans =
0.
-0.2
--> Uc = cont_mat(A, B) // controllability matrix
Uc =
0. 0.1
0.1 -0.02
--> rank(Uc)
ans =
2.
--> Uo = obsv_mat(A, C) // observability matrix
Uo =
1. 0.
0. 1.
--> rank(Uo)
ans =
2.
--> det(Uo)
ans =
1.
--> // state space representation(discrete time system)
--> T = 0.001; // sampling period [s]
--> [Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
--> abs(spec(Ad)) // stability
ans =
1.
0.9998
--> Uc = cont_mat(Ad, Bd) // controllability matrix
Uc =
5.000D-08 0.0000001
0.0001 0.0001
--> rank(Uc)
ans =
2.
--> det(Uc)
ans =
-9.998D-12
--> Uo = obsv_mat(Ad, C) // observability matrix
Uo =
1. 0.
1. 0.0009999
--> rank(Uo)
ans =
2.
--> det(Uo)
ans =
0.0009999
|
octave:1> % physical parameters
octave:1> m = 10; % [kg]
octave:2> d = 2.0; % [N/(m/s)]
octave:3> % state space representation(continuous time system)
octave:3> A = [0 1; 0 -d/m]; B = [0; 1/m];
octave:4> C = [1 0]; D = 0;
octave:5> real(eig(A)) % stability
ans =
0.00000
-0.20000
octave:6> pkg load control
octave:7> Uc = ctrb(A, B) % controllability matrix
Uc =
0.00000 0.10000
0.10000 -0.02000
octave:8> rank(Uc)
ans = 2
octave:9> det(Uc)
ans = -0.010000
octave:10> Uo = obsv(A, C) % observability matrix
Uo =
1 0
0 1
octave:11> rank(Uo)
ans = 2
octave:12> det(Uo)
ans = 1
octave:13> % state space representation(discrete time system)
octave:13> T = 0.001; % sampling period [s]
octave:14> c2d(ss(A, B, C, D), T); Ad = ans.A; Bd = ans.B;
octave:15> abs(eig(Ad)) % stability
ans =
1.00000
0.99980
octave:16> Uc = ctrb(Ad, Bd) % controllability matrix
Uc =
0.000000049997 0.000000149977
0.000099990001 0.000099970005
octave:17> rank(Uc)
ans = 2
octave:18> det(Uc)
ans = -9.9980e-12
octave:19> Uo = obsv(Ad, C) % observability matrix
Uo =
1.00000 0.00000
1.00000 0.00100
octave:20> rank(Uo)
ans = 2
octave:21> det(Uo)
ans = 0.00099990
|
状態フィードバック制御
状態変数 \( \boldsymbol x \) はすべて観測できるものとする(CLSS/DLSS ブロックの設定では \( C \) を単位行列、\( D \) をゼロ行列として、ゲインブロックとして \( C \) 行列を外に出している)
| 連続時間システム | 離散時間システム |
|---|
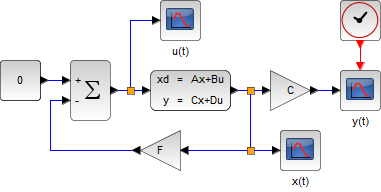 | 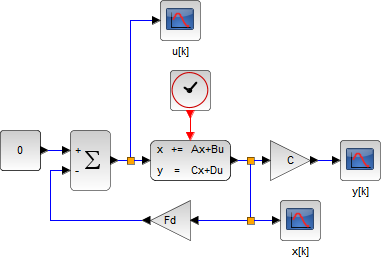 |
ここで、\( F \)、\( F_d \) は、状態フィードバックゲイン
極配置法による Xcos の「コンテキスト設定」
| Xcos |
|---|
// physical parameters
m = 10; // [kg]
d = 2.0; // [N/(m/s)]
// state space representation(continuous time system)
A = [0 1; 0 -d/m];
B = [0; 1/m];
C = [1 0];
D = 0;
// pole placement(continuous time system)
p1 = -2; p2 = -3;
F = ppol(A, B, [p1, p2]);
// state space representation(discrete time system)
T = 0.001 // sampling period [s]
[Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
// pole placement(discrete time system)
p1 = exp(p1*T); p2 = exp(p2*T);
Fd = ppol(Ad, Bd, [p1, p2]);
// initial state
x = 0.5; // [m]
v = 1.5; // [m/s]
x0 = [x; v];
|
(連続時間システムの極と等価な離散時間システムの極について)《積み残し》
(Xcos のプログラム)
LQR 制御による Xcos の「コンテキスト設定」
| Xcos |
|---|
// physical parameters
m = 10; // [kg]
d = 2.0; // [N/(m/s)]
// state space representation(continuous time system)
A = [0 1; 0 -d/m];
B = [0; 1/m];
C = [1 0];
D = 0;
// LQR(continuous time system)
Q = diag([1000, 10]); R = 1;
C1 = [sqrtm(Q); zeros(1,2)];
D12 = [zeros(2,1); sqrtm(R)];
F = -lqr(syslin("c", A, B, C1, D12), Q, R);
// state space representation(discrete time system)
T = 0.001 // sampling period [s]
[Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
// LQR(discrete time system)
Fd = -lqr(syslin("d", Ad, Bd, C1, D12), Q, R);
// initial state
x = 0.5; // [m]
v = 1.5; // [m/s]
x0 = [x; v];
|
(Xcos のプログラム。ブロック線図は極配置法と同じ)
レギュレータの極
(制御系の極)\( A - BF \) の固有値
| Scilab | Octave |
|---|
--> // physical parameters
--> m = 10; // [kg]
--> d = 2.0; // [N/(m/s)]
--> // state space representation(continuous time system)
--> A = [0 1; 0 -d/m]; B = [0; 1/m];
--> C = [1 0]; D = 0;
--> // LQR(continuous time system)
--> Q = diag([1000, 10]); R = 1;
--> C1 = [sqrtm(Q); zeros(1,2)];
--> D12 = [zeros(2,1); sqrtm(R)];
--> F = -lqr(syslin("c", A, B, C1, D12), Q, R);
--> // pole of regulator(continuous time system)
--> pole = spec(A - B*F)
pole =
-1.2712745 + 1.2434383i
-1.2712745 - 1.2434383i
--> real(pole) // stability
ans =
-1.2712745
-1.2712745
--> // state space representation(discrete time system)
--> T = 0.001; // sampling period [s]
--> [Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
--> // LQR(discrete time system)
--> Fd = -lqr(syslin("d", Ad, Bd, C1, D12), Q, R);
--> // pole of regulator(discrete time system)
--> exp(pole*T)
ans =
0.9987288 + 0.0012419i
0.9987288 - 0.0012419i
--> pole = spec(Ad - Bd*Fd)
pole =
0.9987288 + 0.0012419i
0.9987288 - 0.0012419i
--> abs(pole) // stability
ans =
0.9987295
0.9987295
|
octave:1> % physical parameters
octave:1> m = 10; % [kg]
octave:2> d = 2.0; % [N/(m/s)]
octave:3> % state space representation(continuous time system)
octave:3> A = [0 1; 0 -d/m]; B = [0; 1/m];
octave:4> C = [1 0]; D = 0;
octave:5> % LQR(continuous time system)
octave:5> Q = diag([1000, 10]); R = 1;
octave:6> pkg load control
octave:7> F = lqr(A, B, Q, R);
octave:8> % pole of regulator(continuous time system)
octave:8> pole = eig(A - B*F)
pole =
-1.2713 + 1.2434i
-1.2713 - 1.2434i
octave:9> real(pole) % stability
ans =
-1.2713
-1.2713
octave:10> % state space representation(discrete time system)
octave:10> T = 0.001; % sampling period [s]
octave:11> c2d(ss(A, B, C, D), T); Ad = ans.A; Bd = ans.B;
octave:12> % LQR(discrete time system)
octave:12> Fd = dlqr(Ad, Bd, Q, R);
octave:13> % pole of regulator(discrete time system)
octave:13> exp(pole*T)
ans =
0.99873 + 0.00124i
0.99873 - 0.00124i
octave:14> pole = eig(Ad - Bd*Fd)
pole =
0.99873 + 0.00124i
0.99873 - 0.00124i
octave:15> abs(pole) % stability
ans =
0.99873
0.99873
|
サーボシステム
(1型サーボ系)
| 連続時間システム | 離散時間システム |
|---|
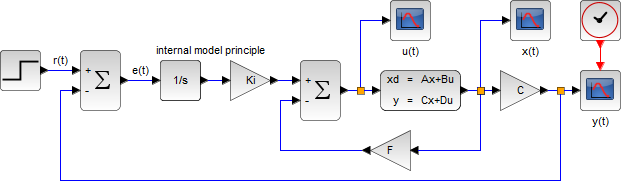 | 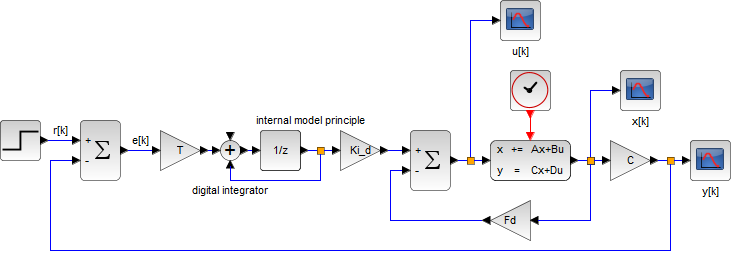 |
極配置法による Xcos の「コンテキスト設定」
| Xcos |
|---|
// physical parameters
m = 10; // [kg]
d = 2.0; // [N/(m/s)]
// state space representation(continuous time system)
A = [0 1; 0 -d/m]; B = [0; 1/m];
C = [1 0]; D = 0;
A_tilde = [A zeros(2, 1); -C 0];
B_tilde = [B; 0];
// pole placement(continuous time system)
p1 = -2; p2 = -3; p3 = -4;
F_tilde = ppol(A_tilde, B_tilde, [p1, p2, p3]);
F = F_tilde(1:2); Ki = -F_tilde(3);
// state space representation(discrete time system)
T = 0.001; // sampling period [s]
[Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
Ad_tilde = [Ad zeros(2, 1); -C*T 1];
Bd_tilde = [Bd; 0];
// pole placement(discrete time system)
pd1 = exp(p1*T); pd2 = exp(p2*T); pd3 = exp(p3*T);
Fd_tilde = ppol(Ad_tilde, Bd_tilde, [pd1, pd2, pd3]);
Fd = Fd_tilde(1:2); Ki_d = -Fd_tilde(3);
// initial state
x = 0.0; // [m]
v = 0.0; // [m/s]
x0 = [x; v];
|
プログラム中の変数名 A_tilde、B_tilde で、拡大系を構成
(Xcos のプログラム)
LQR 制御による Xcos の「コンテキスト設定」
| Xcos |
|---|
// physical parameters
m = 10; // [kg]
d = 2.0; // [N/(m/s)]
// state space representation(continuous time system)
A = [0 1; 0 -d/m]; B = [0; 1/m];
C = [1 0]; D = 0;
A_tilde = [A zeros(2, 1); -C 0];
B_tilde = [B; 0];
// LQR(continuous time system)
Q = diag([1e2, 2e1, 3e4]); R = 1;
C1 = [sqrtm(Q); zeros(1,3)];
D12 = [zeros(3,1); sqrtm(R)];
F_tilde = -lqr(syslin("c", A_tilde, B_tilde, C1, D12), Q, R);
F = F_tilde(1:2); Ki = -F_tilde(3);
// state space representation(discrete time system)
T = 0.001; // sampling period [s]
[Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
Ad_tilde = [Ad zeros(2, 1); -C*T 1];
Bd_tilde = [Bd; 0];
// LQR(discrete time system)
Fd_tilde = -lqr(syslin("d", Ad_tilde, Bd_tilde, C1, D12), Q, R);
Fd = Fd_tilde(1:2); Ki_d = -Fd_tilde(3);
// initial state
x = 0.0; // [m]
v = 0.0; // [m/s]
x0 = [x; v];
|
(Xcos のプログラム。ブロック線図は極配置法と同じ)
(離散時間システムの拡大系について)《教科書など》
オブザーバ
Xcos で実装するオブザーバの式\[ \boxed{
\dot{\hat{\boldsymbol x}}(t) = \big(A - HC\big)\hat{\boldsymbol x}(t) + \begin{bmatrix} B & H \end{bmatrix}\begin{bmatrix} u(t) \\ y(t) \end{bmatrix}
} \]ここで \( \hat{\boldsymbol x} \) は、オブザーバによる状態変数 \( \boldsymbol x \) の推定値。\( H \) はオブザーバゲイン《詳細は教科書など》
これを、状態方程式として見る。つまり\[ \begin{gather}
\bar A = A - HC, \quad \bar B = \begin{bmatrix} B & H \end{bmatrix}
\end{gather} \]この式の形で、CLSS/DLSS パレットに設定する(また、出力方程式には何も作用をさせない。\( C \) 行列は単位行列、\( D \) 行列はゼロ行列)
状態変数の推定値 \( \hat{\boldsymbol x} \) を使って状態フィードバック制御を行う(併合系について)
| 連続時間システム | 離散時間システム |
|---|
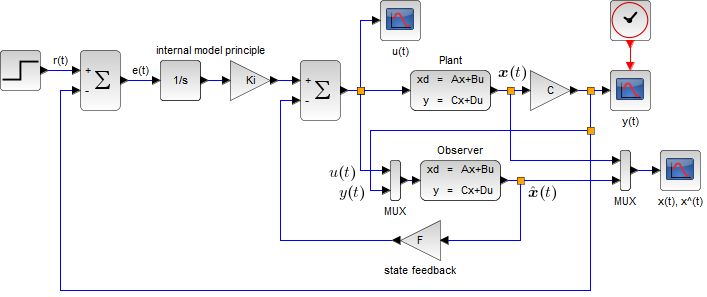 | 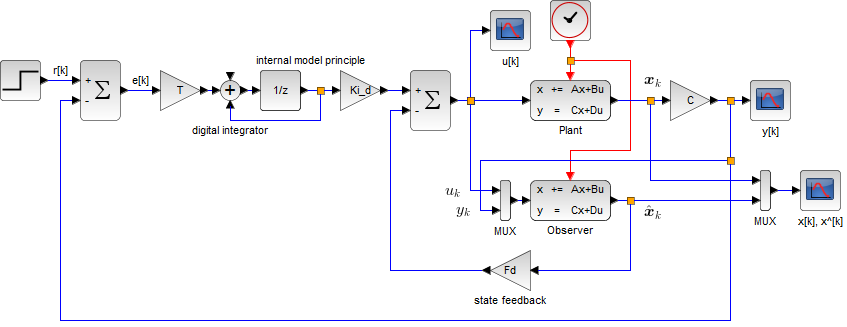 |
ブロック線図で Plant が制御対象(ここでは台車のモデル)
Xcos の「コンテキスト設定」
| Xcos |
|---|
// physical parameters
m = 10; // [kg]
d = 2.0; // [N/(m/s)]
// state space representation(continuous time system)
A = [0 1; 0 -d/m]; B = [0; 1/m];
C = [1 0]; D = 0;
// Observer(continuous time system)
p = [-5, -6] // pole of observer
H = ppol(A', C', p)';
A_tilde = [A zeros(2, 1); -C 0];
B_tilde = [B; 0];
// LQR(continuous time system)
Q = diag([1e2, 2e1, 3e4]); R = 1;
C1 = [sqrtm(Q); zeros(1,3)];
D12 = [zeros(3,1); sqrtm(R)];
F_tilde = -lqr(syslin("c", A_tilde, B_tilde, C1, D12), Q, R);
F = F_tilde(1:2); Ki = -F_tilde(3);
// state space representation(discrete time system)
T = 0.001; // sampling period [s]
[Ad, Bd] = abcd(dscr(syslin("c", A, B, C, D), T));
// Observer(discrete time system)
p = [exp(p(1)*T), exp(p(2)*T)] // pole of observer
Hd = ppol(Ad', C', p)';
Ad_tilde = [Ad zeros(2, 1); -C*T 1];
Bd_tilde = [Bd; 0];
// LQR(discrete time system)
Fd_tilde = -lqr(syslin("d", Ad_tilde, Bd_tilde, C1, D12), Q, R);
Fd = Fd_tilde(1:2); Ki_d = -Fd_tilde(3);
// initial state
x = 1.0; // [m]
v = 0.2; // [m/s]
x0 = [x; v];
|
オブザーバの極は極配置法により、フィードバック制御系の極はLQR 制御により、ぞれぞれのフィードバックゲインを決定している
「パレット」の設定
| | 連続時間システム | 離散時間システム |
|---|
| 制御対象 | CLSS | 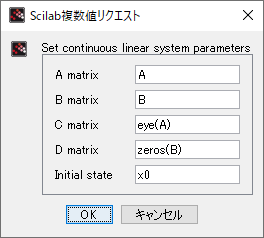 | DLSS | 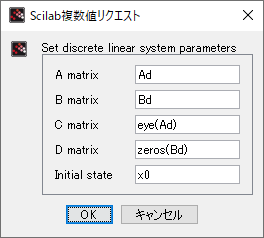 |
|---|
| オブザーバ | CLSS | 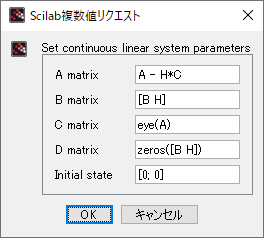 | DLSS | 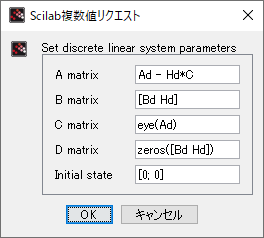 |
|---|
また、オブザーバの初期状態は(制御対象についての情報が無いものと考えて)\( \mathbf 0 \) としている
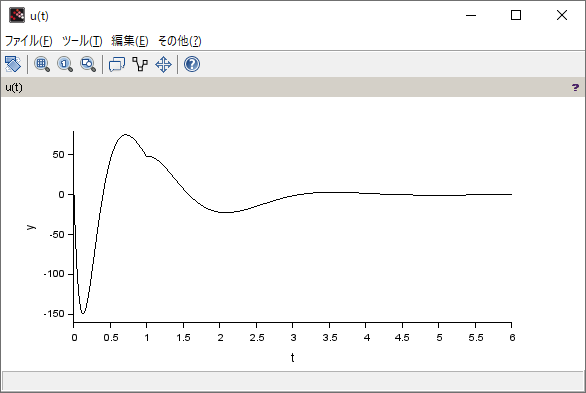
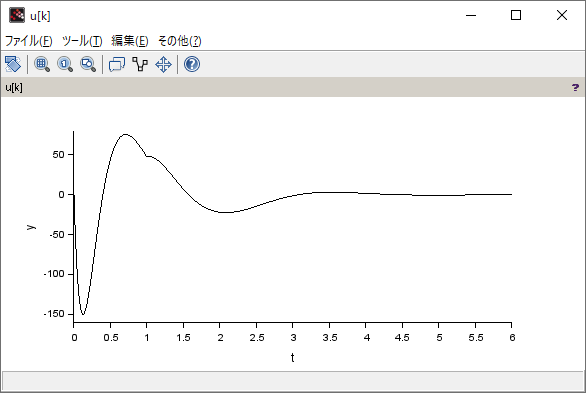
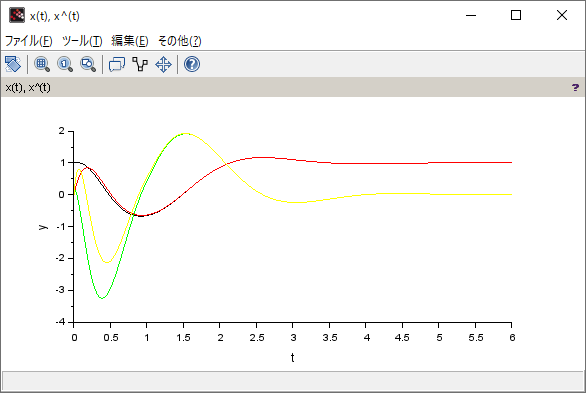
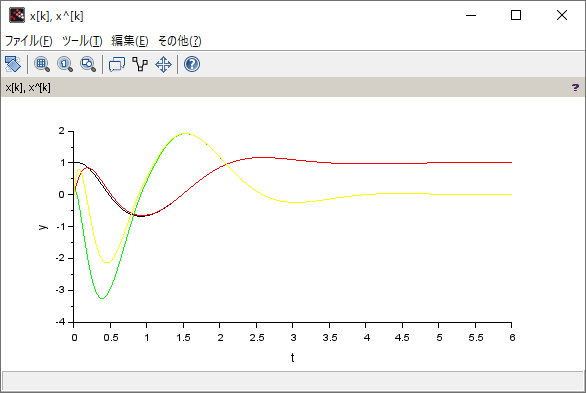
シミュレーション結果
(Xcos のプログラム)
参考文献
© 2023 Tadakazu Nagai