永井 忠一 2020.10.24
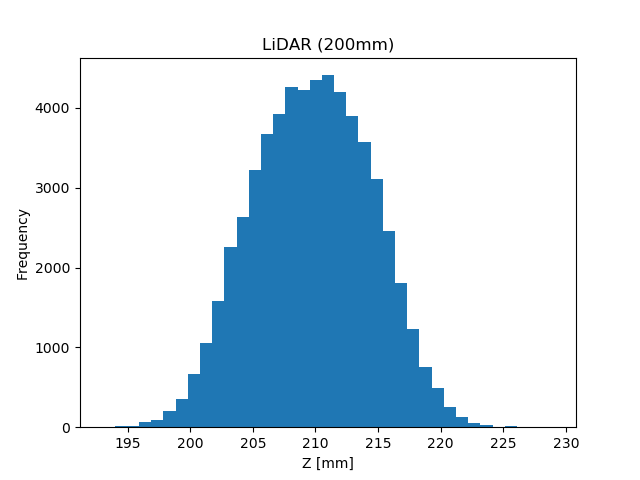
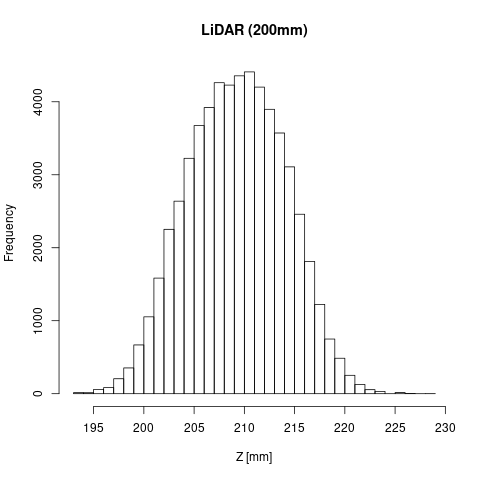
実験データは、こちらにある『sensor_data/sensor_data_200.txt』を使用
 |  |
| Python | R言語 |
|---|---|
|
|
DataFrame/Series の describe() と、R言語の summary() 関数を利用
| IPython | Emacs Speaks Statistics (ESS) |
|---|---|
|
|
扱っているセンサーの平均値は 209.7[mm]、標準偏差は 4.8[mm]
プログラムと実行結果
| Python | R言語 |
|---|---|
|
|
|
|
※ライブラリの分散は「不偏分散」を求める。(サンプル分散ではない)
(R言語には、最頻値を求める関数が見当たらない。)
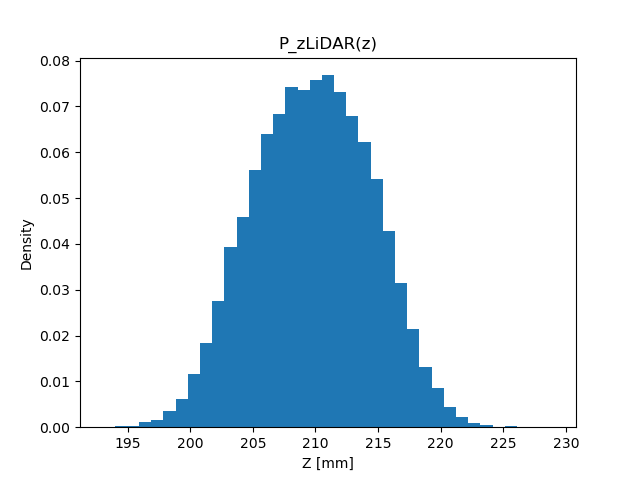
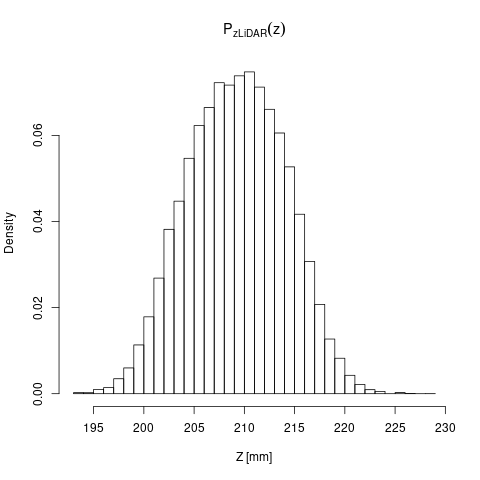
頻度ではなく割合を考える \( P_{\mathbf{z}\text{LiDAR}}(z) = N_z / N \)(\( N_z \): センサー値が \( z \) だった頻度、\( N \): 実験の回数)
 |  |
| Python | R言語 |
|---|---|
|
|
この関数を確率と呼ぶ(確率の定義)(縦軸の値が違うだけ)(histogram を正規化したもの)
|
|
| \[ \mathbb V[z] = \mathbb E\left[(z - \mu)^2\right] = \sigma^2 \] |
こちらにあるデータ『sensor_data/sensor_data_600.txt』を使用
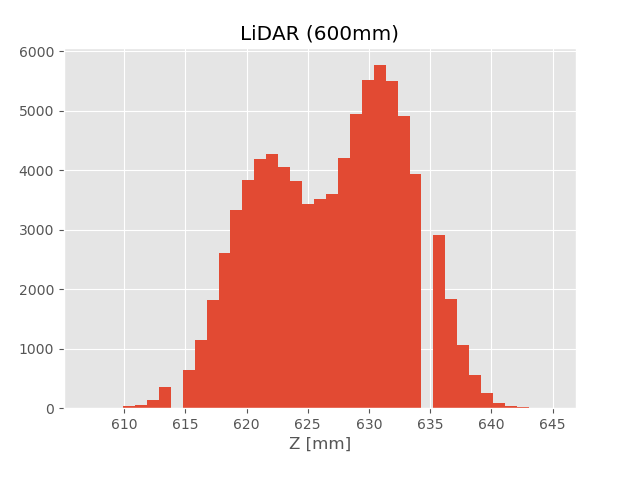
ソースコード
| Python |
|---|
|
614, 635 の頻度がゼロになっている
|
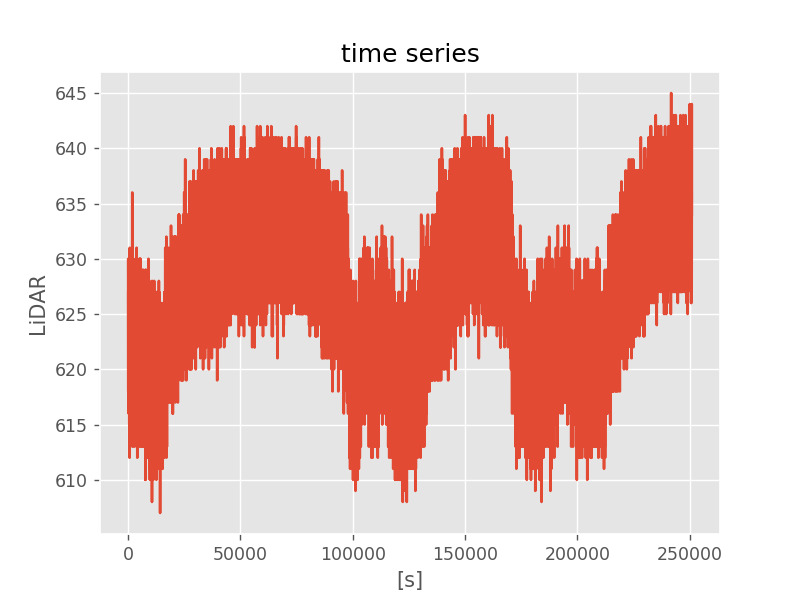
ソースコード
|
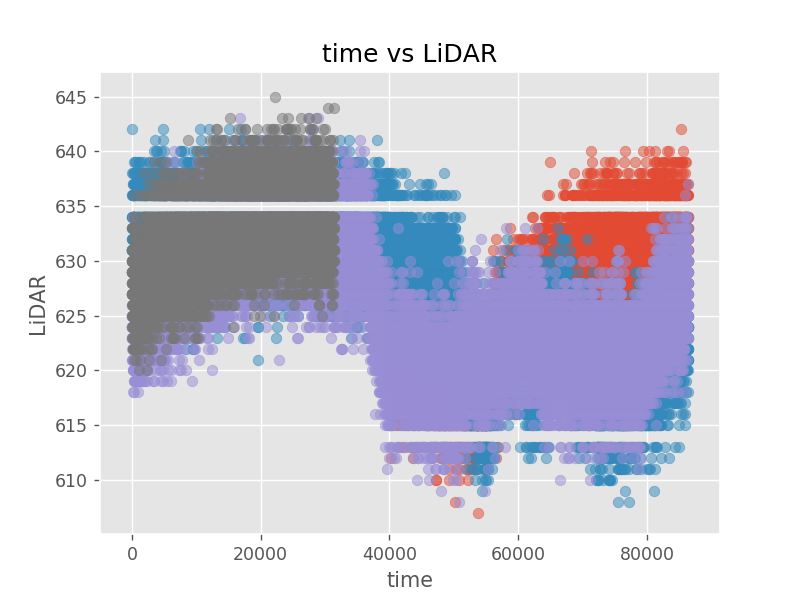 | 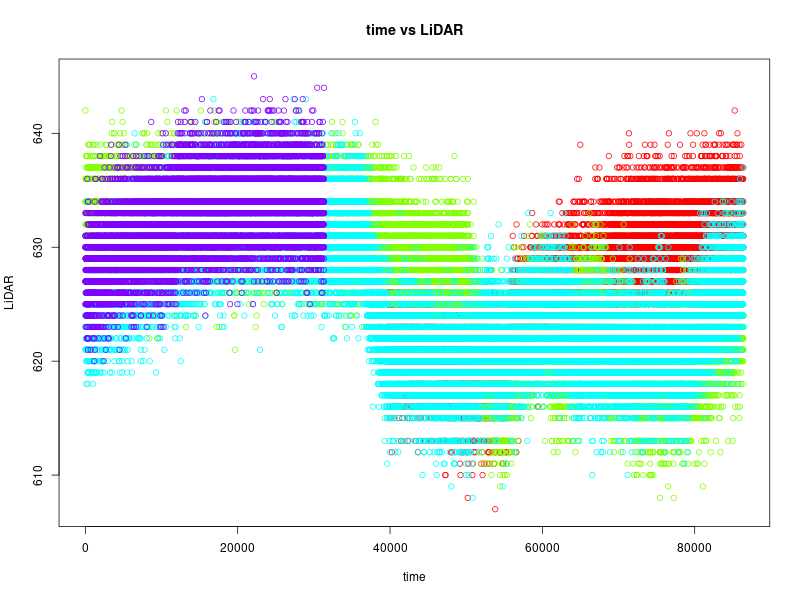 |
ソースコード
| Python | R言語 |
|---|---|
|
|
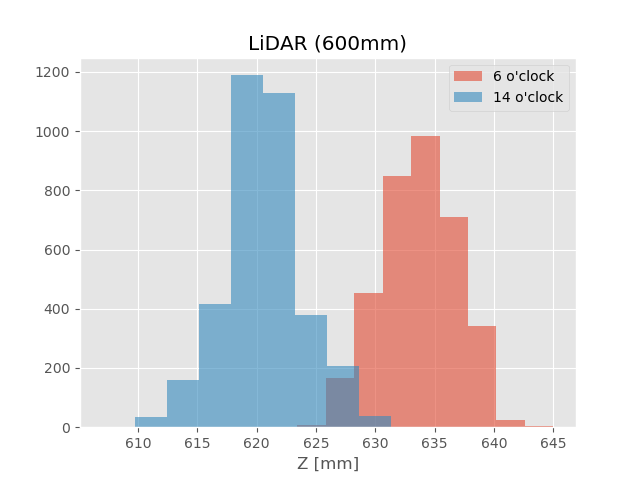 |
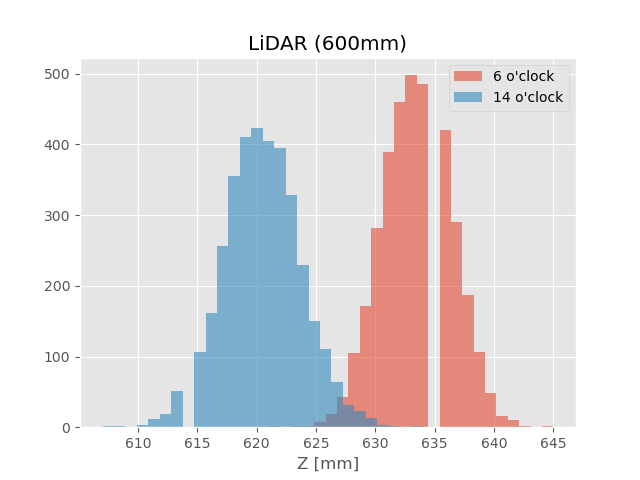 |
(上図:ビンの数はライブラリのデフォルト、下図:ビンの幅を1とした(条件付きの)histogram)
ソースコード
| Python |
|---|
|
6時台のセンサー値の確率分布の表記の例\[ P(z|t \in \text{6 o'clock}) \]
一般的な条件付き確率の表記
「時刻 \( t \) でセンサー値 \( z \) となる確率」。同時確率の表記\[ P(z, t) \](確率なので \( \sum_z\sum_t P(z, t) = 1 \) となる。)
使用するライブラリのインストール(私の環境では、Linux apt)
| Linux apt |
|---|
|
|
同じデータを heatmap で描画
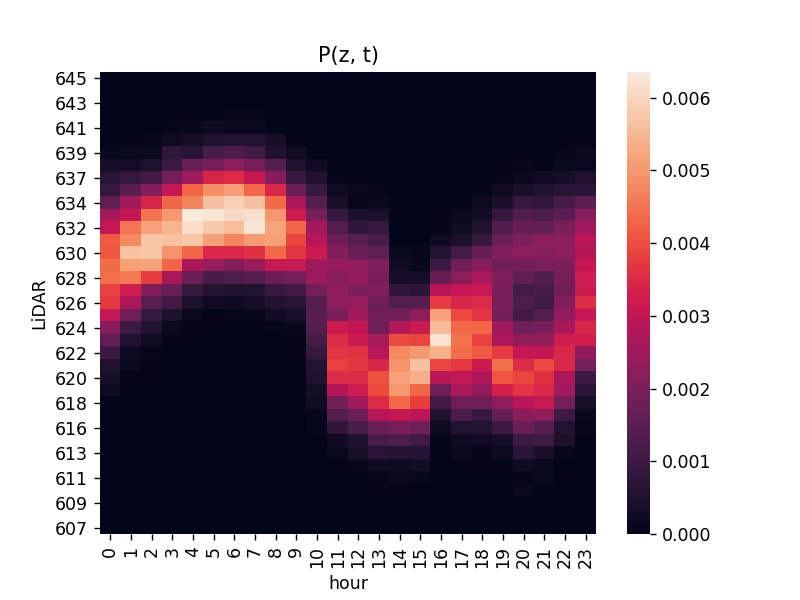
ソースコード
| Python |
|---|
|
seaborn の jointplot() を利用
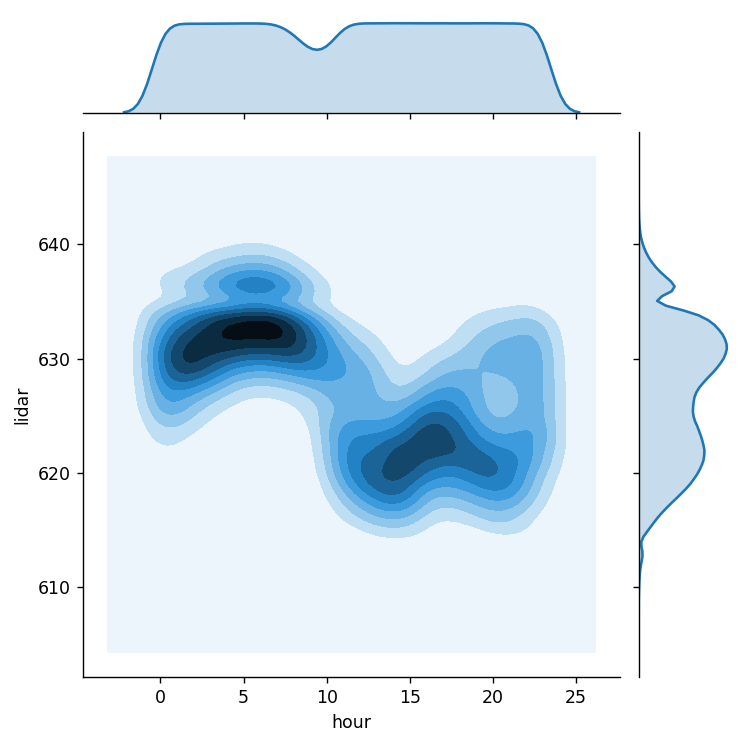
| Python |
|---|
|
同時確率(の表) \( P(z, t) \) から、周辺確率 \( P(z) \)、\( P(t) \) を(プログラムで)求める(周辺化する)
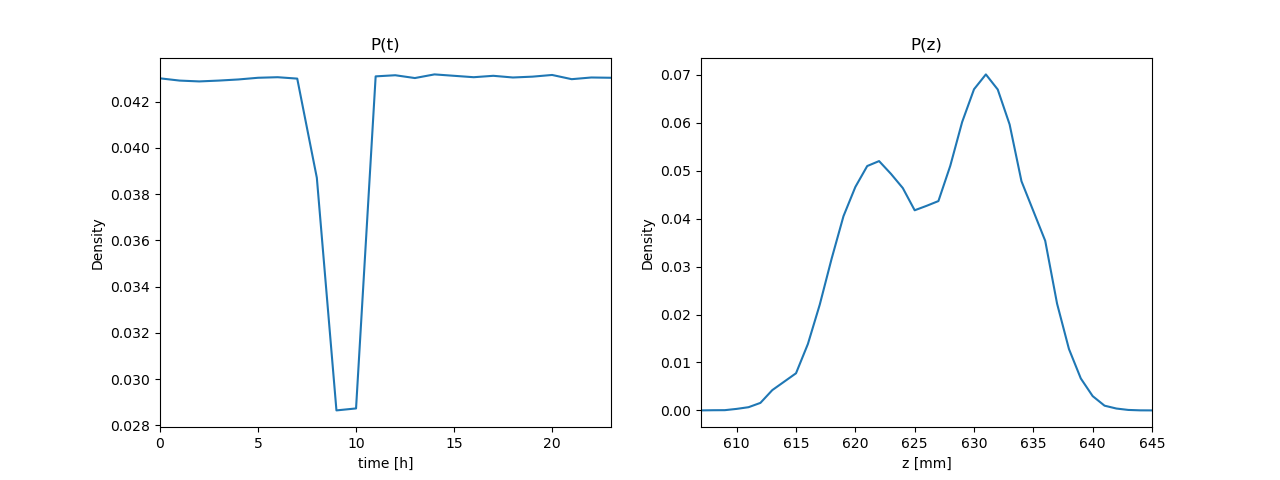
ソースコード
| Python |
|---|
|
確率の加法定理
|
確率の乗法定理
確率変数が3変数以上の乗法定理
(3変数以上の場合、確率変数がベクトルになっていると考える) |
(確率変数どうしの関係性)
独立。条件付き確率において、条件 \( y \) が \( x \) の確率に何も影響を与えない場合、次式が成り立つ\[ p(x|y) = p(x) \]つまり、\( y \) が \( x \) に対して何も情報を与えない
乗法定理に上式を代入\[ p(x, y) = p(x|y)p(y) \Longrightarrow p(x, y) = p(x)p(y) \]この関係を \( x, y \) とが互いに独立と表現
(表記。独立の記号が TEX に無い)
条件付き独立。\( z \) が分かっている(\( z \) が観測された)とき、\( x \) に対して \( y \) が何も情報を与えない
(条件付き独立について)《復習》
(ルベグ積分(ルベーグ積分)、無限と集合(無限の集合)、測度論、フビニの定理など)《積み残し》
(確率の性質だけで計算できる)期待値の計算
\( \mathbf z = (x\ y)^\mathrm T \)、\( x \) と \( y \) は独立とする
|
(和の期待値、期待値の和)\[ \begin{align} \langle f(x) + \alpha g(y) \rangle_{p(\mathbf z)} &= \langle f(x) \rangle_{p(\mathbf z)} + \langle\alpha g(y) \rangle_{p(\mathbf z)} \\ &= \langle f(x) \rangle_{p(\mathbf z)} + \alpha\langle g(y) \rangle_{p(\mathbf z)} \\ &= \langle f(x) \rangle_{p(x)p(y)} + \alpha\langle g(y) \rangle_{p(x)p(y)} \\ &= \langle f(x) \rangle_{p(x)} + \alpha\langle g(y) \rangle_{p(y)} \end{align} \] |
(積の期待値、期待値の積)\[ \begin{align} \langle f(x)g(y) \rangle_{p(\mathbf z)} &= \langle f(x)g(y) \rangle_{p(x)p(y)} \\ &= \left\langle\langle f(x)g(y) \rangle_{p(y)}\right\rangle_{p(x)} \\ &= \left\langle f(x)\langle g(y) \rangle_{p(y)}\right\rangle_{p(x)} \\ &= \langle g(y) \rangle_{p(y)}\langle f(x)\rangle_{p(x)} \end{align} \] 得られる関係式\[ \langle g(y) \rangle_{p(y)}\langle f(x) \rangle_{p(x)} = \left\langle \langle f(x)g(y) \rangle_{p(x)} \right\rangle_{p(y)} = \left\langle \langle f(x)g(y) \rangle_{p(y)} \right\rangle_{p(x)} = \langle f(x)g(y) \rangle_{p(x)p(y)} \] |
乗法定理 \( p(z, t) = p(z|t)p(t) = p(t|z)p(z) \) から導出 \[ \begin{align} p(z|t)p(t) &= p(t|z)p(z) \\ p(z|t) &= \frac{p(t|z)p(z)}{p(t)} = \eta p(t|z)p(z) \end{align} \] \( \eta \) は正規化定数(積分して1にするため)
条件付き確率 \( P(z|t) \) を描画。 \( P(z|t=6) \) と \( P(z|t=14) \)
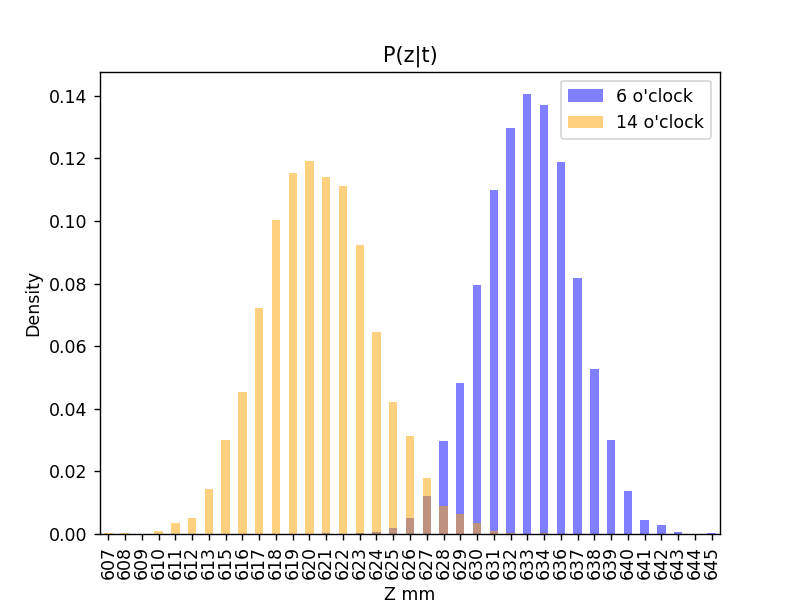
ソースコード
| Python |
|---|
|
ベイズの定理 \( P(z|t) = {P(t|z)P(z)}/{P(t)} \) が成立していることをプログラムで確認
プログラムと実行結果
| Python |
|---|
|
|
センサー値が \( z_1 = 630 \)、\( z_2 = 632 \)、\( z_3 = 636 \) と続けて得られたときの \( P(t|\mathbf z) \) を計算
ベイズの定理\[ \begin{align} P(t|z)P(z) &= P(z|t)P(t) \\ P(t|z) &= \frac{P(z|t)P(t)}{P(z)} = \eta P(z|t)P(t) \end{align} \]より \[ P(t|z_1, z_2, z_3)P(z) = \eta P(z_1, z_2, z_3|t)P(t) \]
さらに、条件付き独立より \[ \begin{align} P(t|z_1, z_2, z_3)P(z) &= \eta P(z_1, z_2, z_3|t)P(t) \\ &= \eta P(z_1|t)P(z_2|t)P(z_3|t)P(t) \end{align} \] (隣り合うサンプル値のように \( t \) がほぼ等しい場合は、 i.i.d. を仮定できる)
\( P(z_1|t) \)、\( P(z_2|t) \)、\( P(z_3|t) \) を逐次掛けていくことで、\( t \) を推定することができる(→ ガウス分布のベイズ推定について)
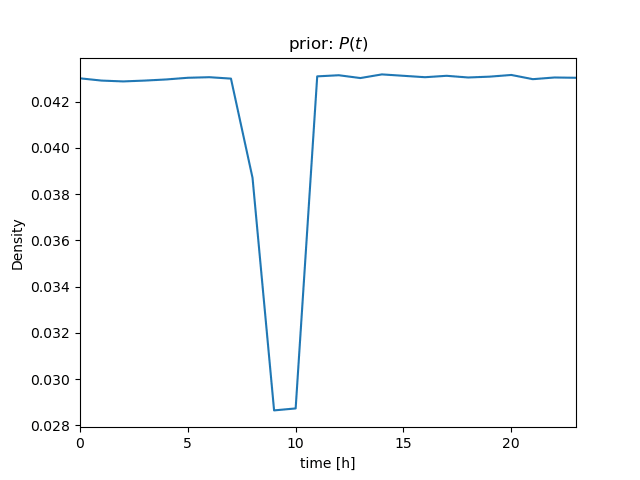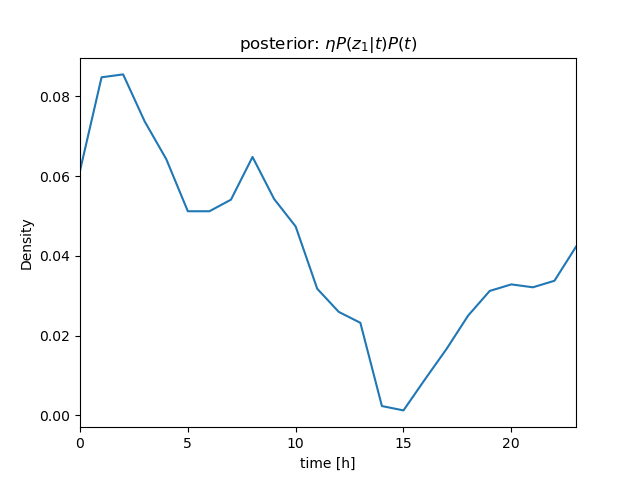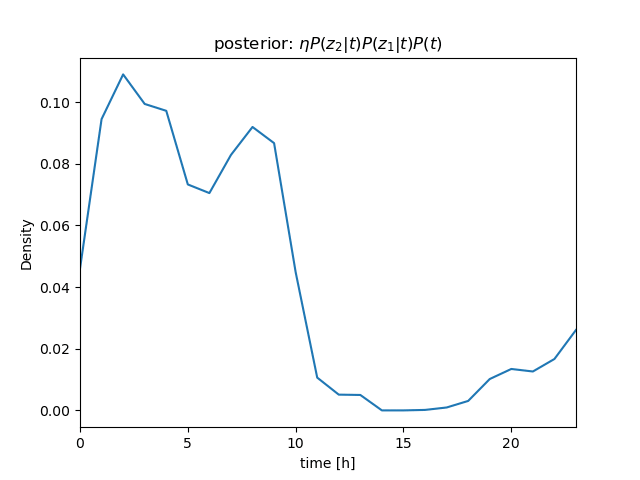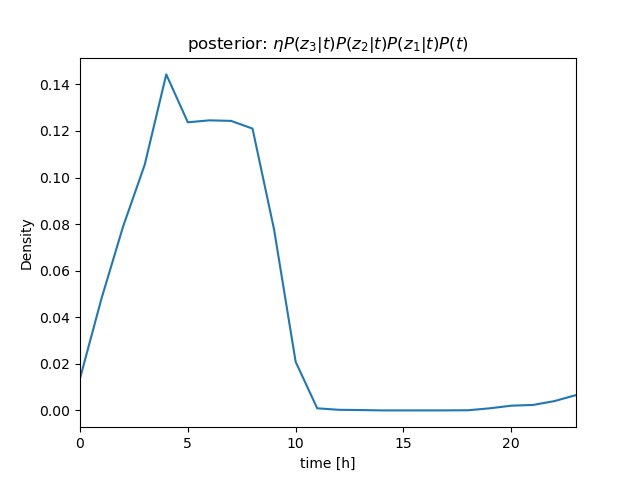
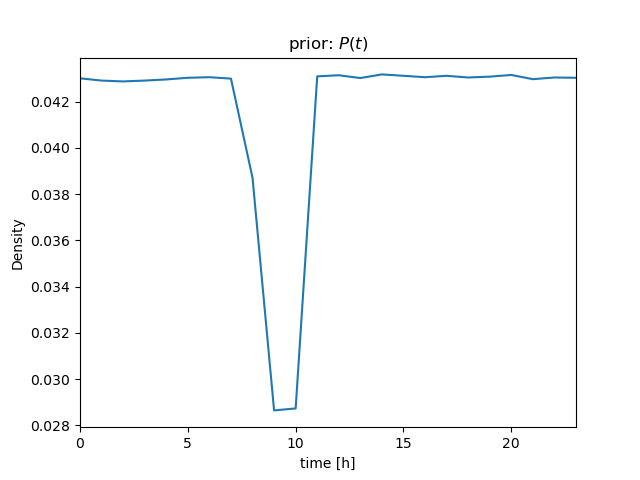
| \( bel \): prior | ||
|---|---|---|
 | ||
| observation | likelihood | \( bel \): posterior/prior |
| \[ z_1 = 630 \] | 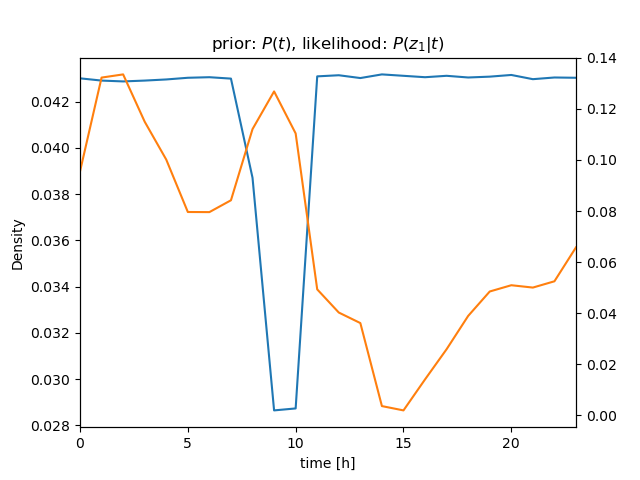 | 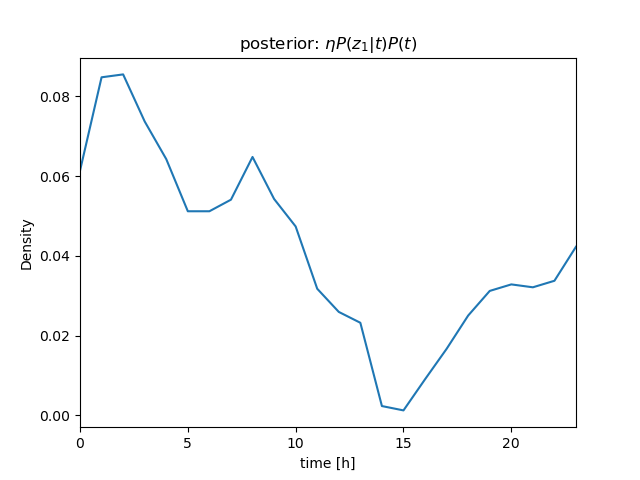 |
| \[ z_2 = 632 \] | 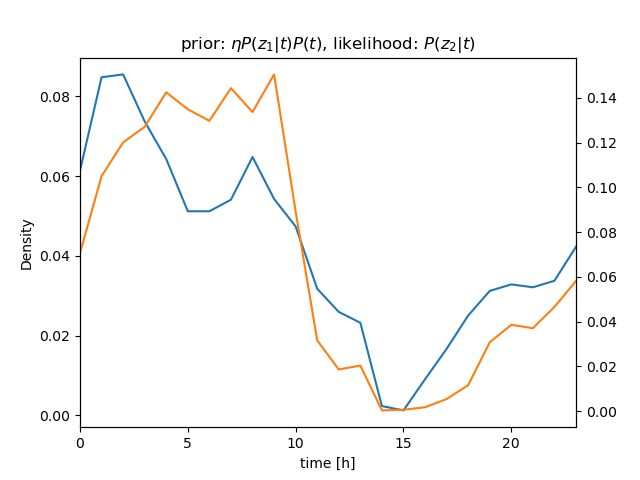 | 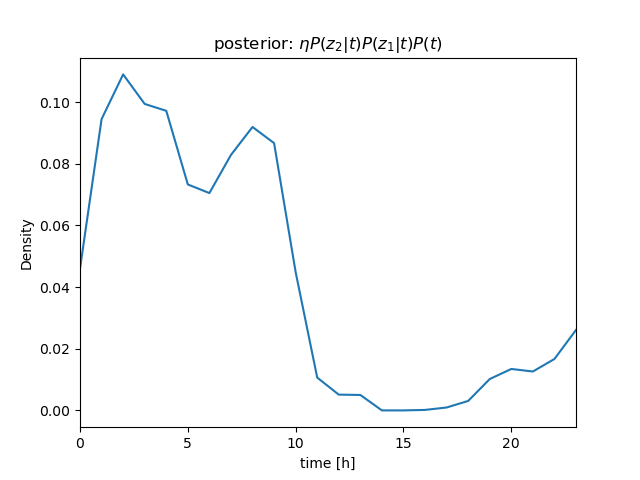 |
| observation | likelihood | \( bel \): posterior |
| \[ z_3 = 636 \] | 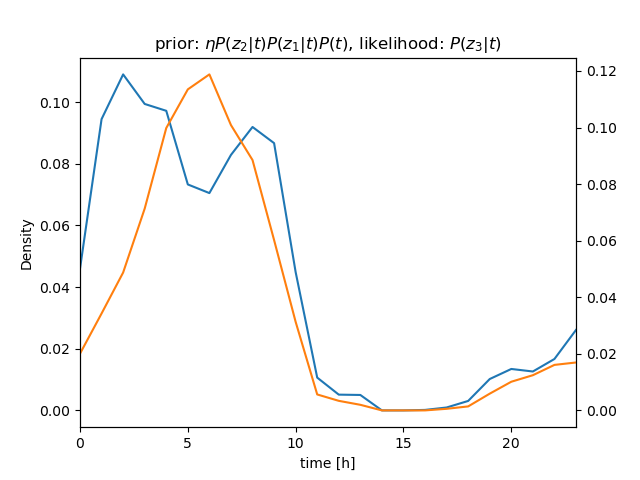 | 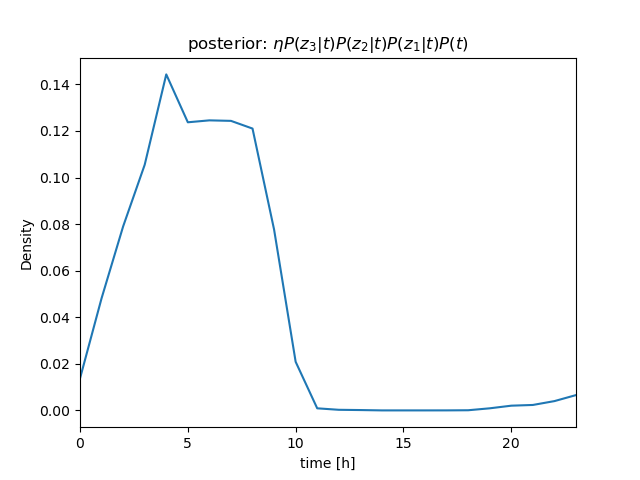 |
ソースコード
| Python |
|---|
|
(推定の結果も分布として求まる)
(尤度(likelihood)について。\( P(z_1 | t) \)、\( P(z_2 | t) \)、\( P(z_3 | t) \) が確率の場合には、\( z_1 \)、\( z_2 \)、\( z_3 \) は確率変数。既に \( z_1 \)、\( z_2 \)、\( z_3 \) が観測された状況で、\( t \) の方を変数だと思って \( P(\boldsymbol{z} | t) \) を見た場合には、\( P(z_1 | t) \)、\( P(z_2 | t) \)、\( P(z_3 | t) \) は尤度(尤度関数)となる)
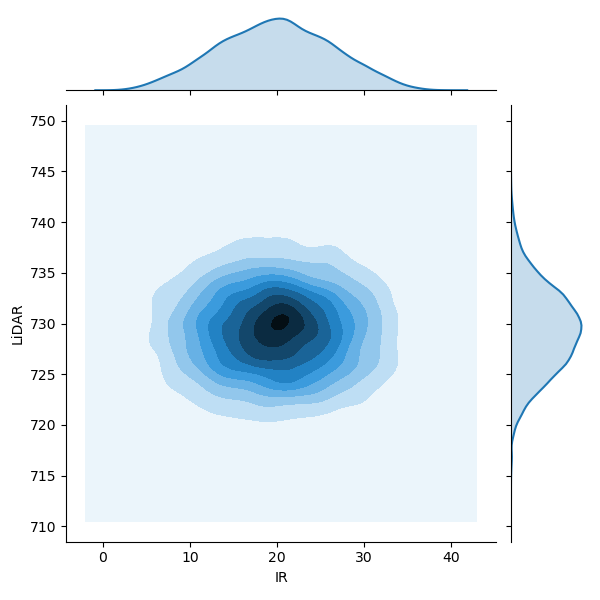
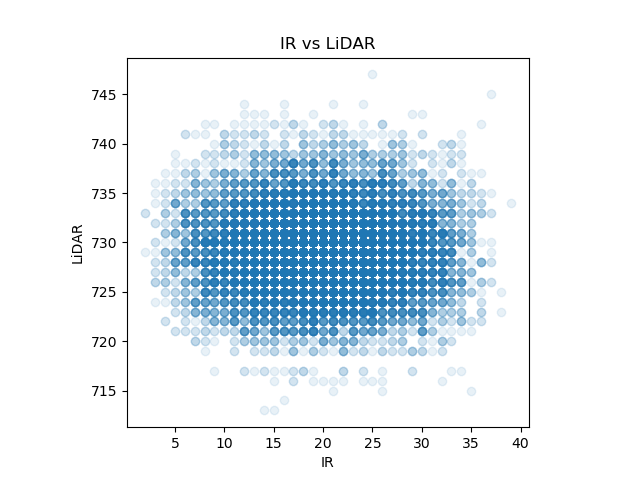
別の実験データ『sensor_data/sensor_data_700.txt』を可視化して、分布を確認
 |
 |
ソースコード
| Python |
|---|
|
(同時分布 \( P(\mathbf z) = P(x, y) \) は(ほぼ丸い)、どちらの確率変数で周辺化してもガウス分布の形をしている)
(多次元のガウス分布は、どの変数を残して周辺化してもガウス分布になる)
\[ \begin{align} \mathcal N(\mathbf z|\boldsymbol\mu, \Sigma) &= \frac{1}{(2\pi)^\frac{n}{2}\sqrt{|\Sigma|}}\exp\left\{-\frac{1}{2}(\mathbf z - \boldsymbol\mu)^\mathrm T\Sigma^{-1}(\mathbf z - \boldsymbol\mu) \right\} \\ &= \eta\exp\left\{ -\frac{1}{2}(\mathbf z - \boldsymbol\mu)^\mathrm T\Sigma^{-1}(\mathbf z - \boldsymbol\mu) \right\} \end{align} \]\( \boldsymbol\mu \):(平均値、分布の)中心(\( n \) 次元)、\( \Sigma \):共分散行列(\( n \times n \) 対称行列)(\( n \) 次対称行列) |
(\( \eta \) は、積分して1にするための正規化定数)
分布の形は \( e \) の指数乗。\( \exp \)
確率の値を一定にして図を描くと(等高線を引くと)楕円になる(楕円の式とも言える)
|
(別の形で式を書く)\[ \mathcal N(\mathbf z|\boldsymbol\mu, \Sigma) = \eta e^{ -\frac{1}{2}(\mathbf z - \boldsymbol\mu)^\mathrm T\Sigma^{-1}(\mathbf z - \boldsymbol\mu) } \] 1次元のガウス分布との比較
形は、\( e^{ -\frac{1}{2}\frac{(z - \mu)^2}{\sigma^2} } \)。対応を見ると、\( \Sigma^{-1} \) は \( \frac{1}{\sigma^2} \)。スカラーの二乗 \( (z - \mu)^2 \) は、ベクトルになると2次形式(quadratic form) \( (\mathbf z - \boldsymbol\mu)^\mathrm T\Sigma^{-1}(\mathbf z - \boldsymbol\mu) \) の形になる (1次元を2次元(多次元)に拡張している。式は難しく見えるが、実は変わっていない) |
 |
ソースコード
| Maxima |
|---|
|
楕円の式を行列で書く\[ \begin{align} \frac{x^2}{a^2} + \frac{y^2}{b^2} &= 1 \\ \begin{pmatrix} x & y \end{pmatrix}\begin{pmatrix} \frac{1}{a^2} & 0 \\ 0 & \frac{1}{b^2} \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} &= 1 \\ \begin{pmatrix} x & y \end{pmatrix}\begin{pmatrix} a^2 & 0 \\ 0 & b^2 \end{pmatrix}^{-1}\begin{pmatrix} x \\ y \end{pmatrix} &= 1 \\ \begin{pmatrix} x \\ y \end{pmatrix}^\mathrm T\begin{pmatrix} a^2 & 0 \\ 0 & b^2 \end{pmatrix}^{-1}\begin{pmatrix} x \\ y \end{pmatrix} &= 1 \end{align} \] 式の形が \( (\mathbf z - \boldsymbol\mu)^\mathrm T\Sigma^{-1}(\mathbf z - \boldsymbol\mu) \) と同じになっている。楕円の形の式だと分かる
式変形の検算
| Maxima |
|---|
|
|
|
2次元の場合
\[ \Sigma = \begin{pmatrix} \sigma_x^2 & \sigma_{xy} \\ \sigma_{yx} & \sigma_y^2 \end{pmatrix} \]\( \sigma_x^2,\ \sigma_y^2 \):\( x,\ y \) の分散、\( \sigma_{xy},\ \sigma_{yx} \):共分散 |
共分散\[ \sigma_{xy} = \sigma_{yx} = \frac{1}{N}\sum_{i = 0}^{N - 1}(x_i - \mu_x)(y_i - \mu_y) \]
(共分散行列は、必ず対称行列になる)
(不偏分散なら \( \frac{1}{N - 1} \) とする。\( \frac{1}{N} \) は、標本分散)(母集団の分散(母分散)を推定しているのか、サンプルの分散(ばらつき)そのものを計算しているのかで使い分ける。\( N \) が大きい場合は誤差で無視できるが、\( N \) が小さい場合には値が変わってくる)
(パラメータ推定)
センサー値『sensor_data/sensor_data_700.txt』から共分散行列の値を計算
プログラムと実行結果
| Python | R言語 |
|---|---|
|
|
|
|
ライブラリ関数による共分散行列の計算
| IPython | Emacs Speaks Statistics (ESS) |
|---|---|
|
|
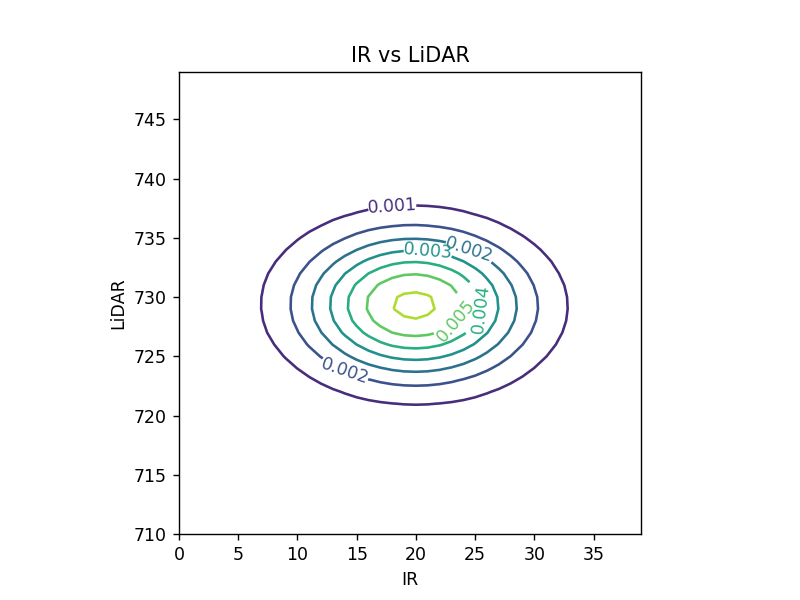
推定されたパラメタ(平均値と共分散行列)\[ \boldsymbol\mu = \begin{pmatrix} 19.86 \\ 729.312 \end{pmatrix},\ \Sigma = \begin{pmatrix} 42.117 & -0.317 \\ -0.317 & 17.702 \end{pmatrix} \]
\( \boldsymbol\mu \) と \( \Sigma \) の値を使って、ガウス分布を描画
 | 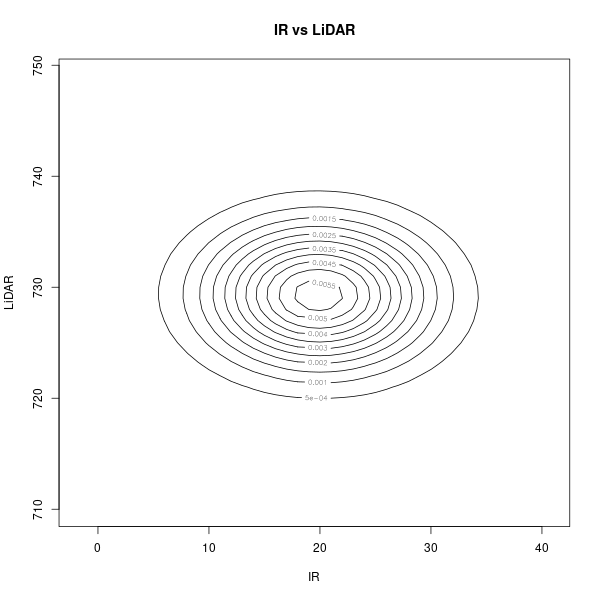 |
ソースコード
| Python | R言語 |
|---|---|
|
|
多次元のガウス分布には、SciPy の multivariate_normal() 関数と、R言語の mvtnorm パッケージの dmvnorm() 関数を利用
(確率密度関数(probability density function, PDF))
R言語の mvtnorm パッケージのインストール(私の環境では Linux apt)
| Linux apt |
|---|
|
2次元のカーネル密度推定結果との比較
| カーネル密度推定 | 2次元のガウス分布 |
|---|---|
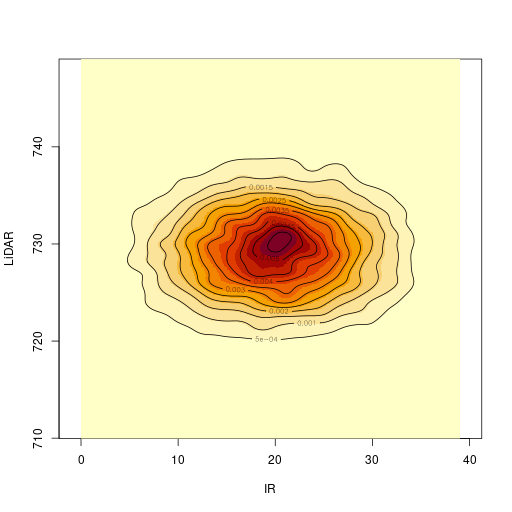 | 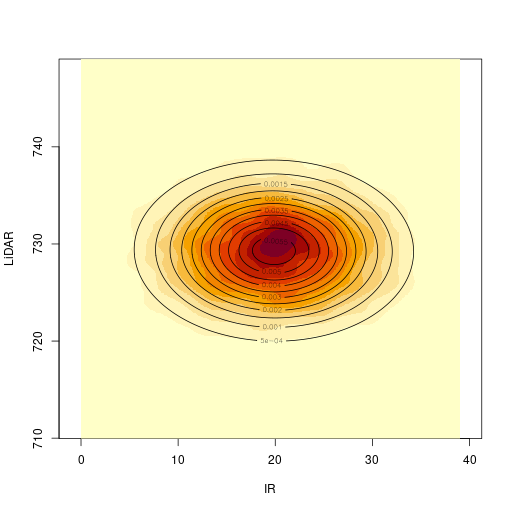 |
ソースコード
| R言語 |
|---|
|
2次元のカーネル密度推定には、R言語の MASS パッケージの kde2d() 関数を利用
R言語の MASS パッケージのインストール(私の環境では Linux apt)
| Linux apt |
|---|
|
使用したデータの散布図を再掲載
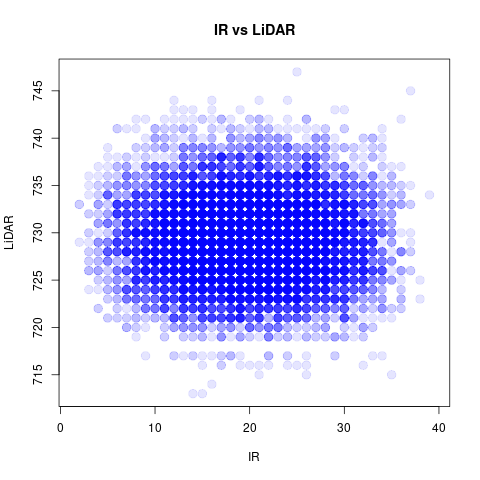
| R言語 |
|---|
|
それぞれ\[ \mathcal N\left[\boldsymbol\mu = \begin{pmatrix} 50\\ 50 \end{pmatrix}, \Sigma = \begin{pmatrix} 50 & 0 \\ 0 & 100 \end{pmatrix} \right],\ \mathcal N\left[\boldsymbol\mu = \begin{pmatrix} 100\\ 50 \end{pmatrix}, \Sigma = \begin{pmatrix} 125 & 0 \\ 0 & 25 \end{pmatrix} \right],\ \mathcal N\left[\boldsymbol\mu = \begin{pmatrix} 150\\ 50 \end{pmatrix}, \Sigma = \begin{pmatrix} 100 & -25\sqrt{3} \\ -25\sqrt{3} & 50 \end{pmatrix} \right] \]のガウス分布を描画
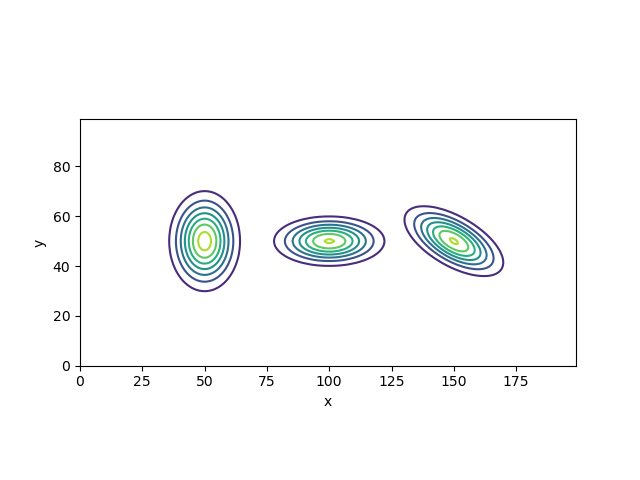
ソースコード
| Python |
|---|
|
分散 \( \sigma_x^2,\ \sigma_y^2 \) が各軸の分布の広がりに対応し、共分散 \( \sigma_{xy} \) に値があると分布が回転することが分かる
ガウス分布の傾き。共分散行列 \( \Sigma \) の固有値と固有ベクトルを求める(→ 固有値と固有ベクトル)
プログラムと実行結果
| Python |
|---|
|
|
計算結果を図示
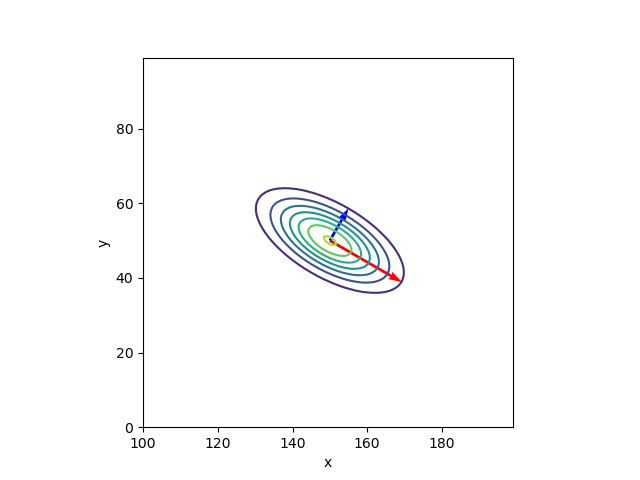
| Python |
|---|
|
共分散行列 \( \Sigma \) と、固有値、固有ベクトルの関係\[ \Sigma = V L V^{-1} \]ここでは、\( V = \begin{pmatrix} \boldsymbol{v}_1 & \boldsymbol{v}_2 \end{pmatrix}\)、\( L = \begin{pmatrix} l_1 & 0 \\ 0 & l_2 \end{pmatrix} \)。計算結果\[ \begin{pmatrix} 100 & -25\sqrt{3} \\ -25\sqrt{3} & 50 \end{pmatrix} = \begin{pmatrix} 0.8660254 & 0.5 \\ -0.5 & 0.8660254 \end{pmatrix} \begin{pmatrix} 125.0 & 0 \\ 0 & 25.0 \end{pmatrix} \begin{pmatrix} 0.8660254 & 0.5 \\ -0.5 & 0.8660254 \end{pmatrix}^{-1} \]
数値計算による確認。プログラムと実行結果
| Python |
|---|
|
|
|
線形代数の復習
|
共分散行列は対角行列を回転行列(と回転行列の逆行列)で挟んだ形に(分解)できる《証明は教科書》
2次元の回転行列\[ R_\theta = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \]
計算結果を回転行列で表現\[ \Sigma = \begin{pmatrix} 0.8660254 & 0.5 \\ -0.5 & 0.8660254 \end{pmatrix} \begin{pmatrix} 125.0 & 0 \\ 0 & 25.0 \end{pmatrix} \begin{pmatrix} 0.8660254 & 0.5 \\ -0.5 & 0.8660254 \end{pmatrix}^{-1} = R_{-\pi/6} \begin{pmatrix} 125.0 & 0 \\ 0 & 25.0 \end{pmatrix} R_{-\pi/6}^{-1} \]
数値計算による確認。プログラムと実行結果
| Python |
|---|
|
|

| Python |
|---|
|
ガウス分布を楕円で描く。たとえば、長軸、短軸を標準偏差を3倍して楕円を描いたもの。標準偏差で正規化されているので、楕円の大きさで分布を比較することができる
3倍の意味。長軸、短軸方向とも \( 3\sigma \)。積分すると
確率変数がガウス分布に従う場合
ガウス分布同士の和
(式の導出。1次元の場合)《導出は教科書》
シミュレーション

| Python |
|---|
|
状態空間、制御出力\[ \boldsymbol{x} \in \mathcal X,\ \boldsymbol{u} \in \mathcal U \](状態変数で表現されたものしか扱えない)(フレーム問題) 離散時間を考える\[ t \in \mathcal T \](状態遷移には時間が掛かる) (雑音を考慮した)状態方程式線形な状態方程式\[ \boldsymbol{x}_t = A\boldsymbol{x}_{t-1} + B\boldsymbol{u}_t + \boldsymbol{\epsilon}_t \]非線形な状態方程式\[ \boldsymbol{x}_t = f(\boldsymbol{x}_{t-1}, \boldsymbol{u}_t) + \boldsymbol{\epsilon}_t \](\( f() \) は状態遷移関数) 状態遷移の確率密度関数(PDF)状態遷移を、確率の式として書く\[ \boldsymbol{x}_t \sim p(\boldsymbol{x} | \boldsymbol{x}_{t-1}, \boldsymbol{u}_t) \] 状態に関する確率密度関数(PDF)\[ bel_t(\boldsymbol{x}) = \int_\mathcal{X} p(\boldsymbol{x} | \boldsymbol{x}’, \boldsymbol{u}_t) bel_{t-1}(\boldsymbol{x}’) d\boldsymbol{x}’ \](\( \boldsymbol{x}’ \) は \( \boldsymbol{x}_{t-1} \) のある1サンプル点)(\( bel \) は belief の略。信念) 積分計算の意味を、シミュレーションで理解
ソースコード
1次元の問題の例状態は1次元 \( x \in \Re \)。制御出力 \( u \) は状態の変位 \( \Delta_t \)(制御出力も状態と同じ次元にある一般的ではない場合)\[ x_t = x_{t - 1} + \Delta_t + \epsilon \]雑音 \( \epsilon \) は標準偏差 \( \delta_t \) でガウス分布に従う この \( bel(x_t) \) の一般解を求める\[ bel(x_t) = \int_{\mathcal X} p(x_t | x_{t-1}, \Delta_t) bel(x_{t-1}) dx_{t-1} \] 以下から導出\[ p(x | x_{t-1}, \Delta_t) = \frac{1}{\sqrt{2\pi\delta^2_t}}\exp\left\{ -\frac{(x - x_{t-1} - \Delta_t)^2}{2\delta^2_t} \right\},\ bel(x_{t-1}) = \frac{1}{\sqrt{2\pi\sigma^2_{t-1}}}\exp\left\{ -\frac{(x_{t-1} - \hat{x}_{t-1})^2}{2\sigma^2_{t-1}} \right\} \]\( \hat{x}_{t-1} \) は \( t - 1 \) における分布の中心(状態の推定値)、\( \sigma_{t-1} \) は \( t - 1 \) における分布の標準偏差 \( bel \) の式にガウス分布を代入\[ bel(x_t) = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\delta^2_t}}\exp\left\{ -\frac{(x - x_{t-1} - \Delta_t)^2}{2\delta^2_t} \right\} \frac{1}{\sqrt{2\pi\sigma^2_{t-1}}}\exp\left\{ -\frac{(x_{t-1} - \hat{x}_{t-1})^2}{2\sigma^2_{t-1}} \right\} dx_{t-1} \] Maxima で記号計算
正規化定数 \( \eta \) を導入して式を整理\[\eta\,e^ {- {{x^2+\left(-2\,\Delta_{t}-2\,{\it \hat{x}}_{t- 1}\right)\,x+\Delta_{t}^2+2\,{\it \hat{x}}_{t-1}\,\Delta_{t}+ {\it \hat{x}}_{t-1}^2}\over{2\,\delta_{t}^2+2\,\sigma_{t-1}^2}} }\](※Maxima の計算結果の TEX を手作業で修正) Maxima の factor() 関数を使って \( e \) の肩の式の形を(ガウス分布として)見やすいように整理
結局 \( bel(x_t) \) は\[ bel(x_t) = \eta\exp\left\{ -\frac{(x - \hat{x}_{x-1} - \Delta_t)^2}{2(\sigma^2_{t-1} + \delta^2_t)} \right\} = \mathcal{N}(\hat{x}_{t-1} + \Delta_t, \sigma^2_{t-1} + \delta^2_t) \]再びガウス分布となる 導出された結論の式の意味の理解
シミュレーション 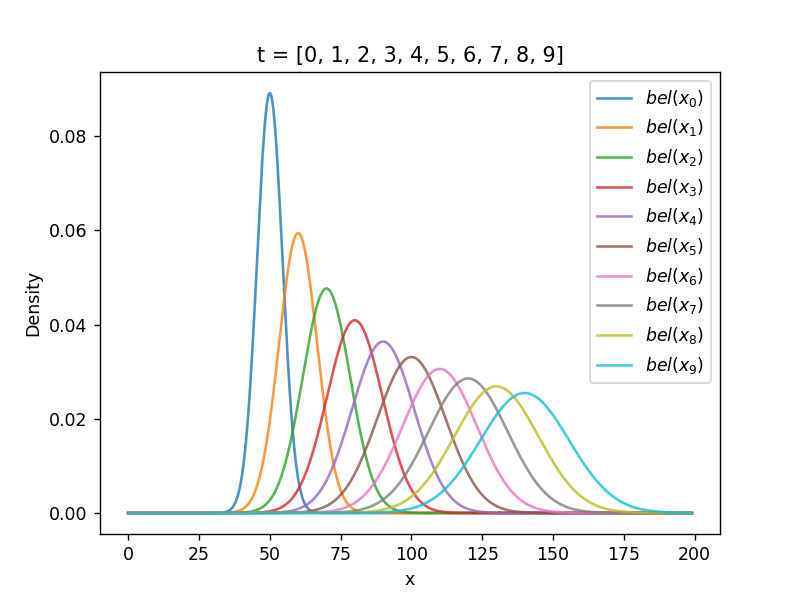 ソースコード
(カルマンフィルターの移動更新 (motion update) の式)(1次元で、いろいろ省略されている) パーティクルフィルター(ガウス分布に従わない場合、数値計算で解く)(モンテカルロ法) 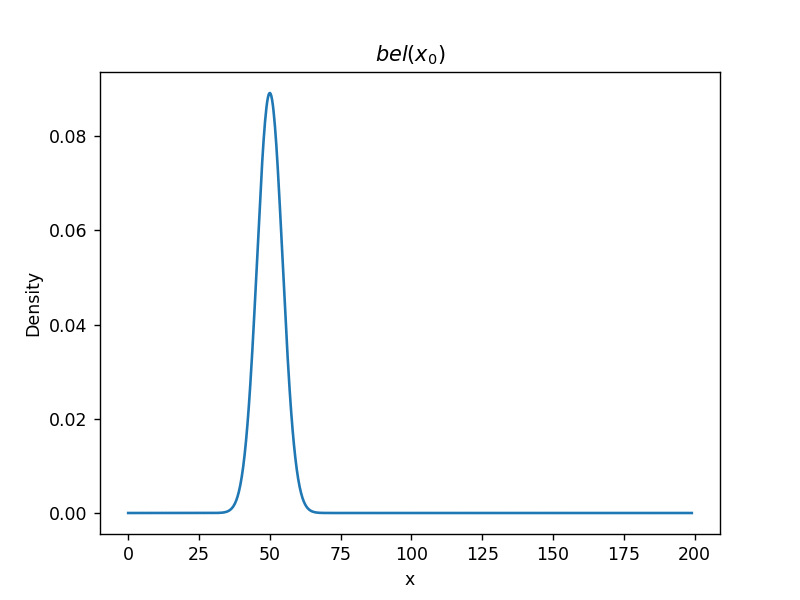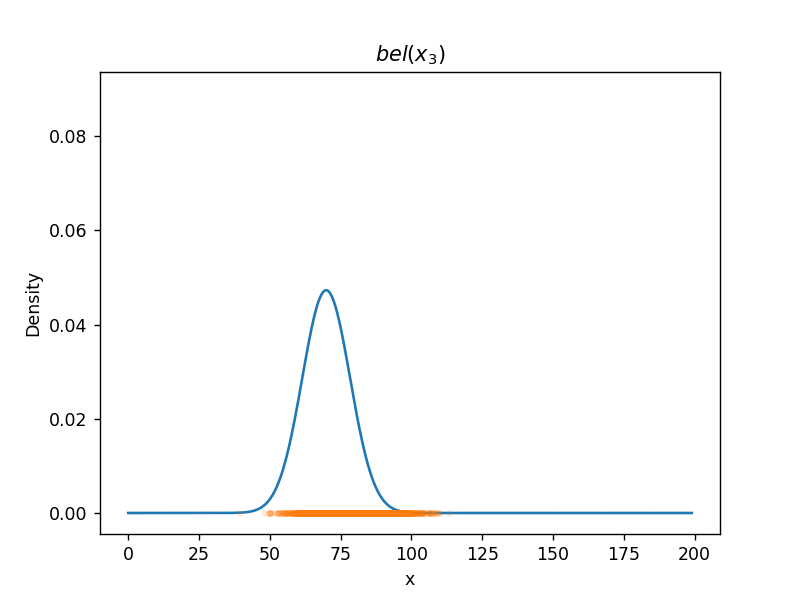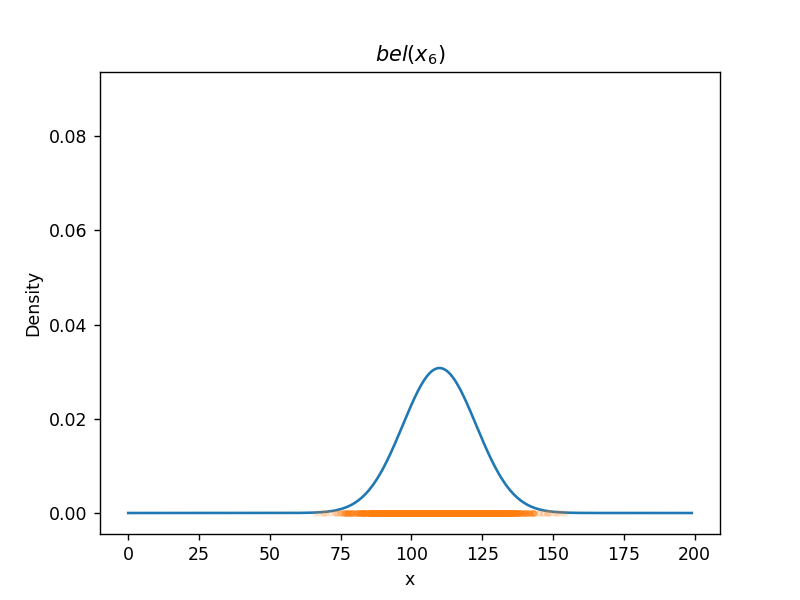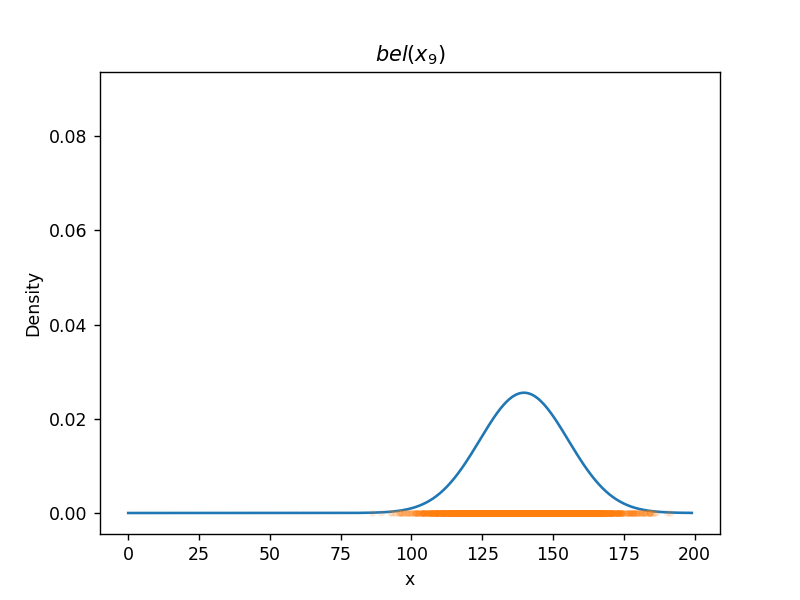 ソースコード
(自己位置推定に使われている、モンテカルロローカライゼーションの移動の式)(乱数を使っている。パーティクル(点)の数が少ないと劣化する) (他にも(格子(格子地図)を使った \( bel \) の計算)「ヒストグラムフィルター」など) 参照資料千葉工業大学の上田隆一先生のスライド『確率ロボティクス2016第1回、第2回』を拝読させていただきました。m(_o_)m |
ガウス分布同士の積
精度行列 \( \Lambda \) を導入(共分散行列 \( \Sigma \) の逆行列)
(式の導出。1次元の場合で、新たな観測の数 \( N \) が一般の場合、と \( N = 1 \) の場合に限定して式変形したもの)《復習》
結論の式の意味の理解。精度は足し算になる。平均値は、精度の重み付き平均になっている(結果は、精度は必ず上がり(分散が小さくなる)、平均値(中心)は精度の良い分布の方に寄る)(ガウス分布同士の掛け算は、結局、ガウス分布になる)
シミュレーション(→ 1次元のベイズ推定)
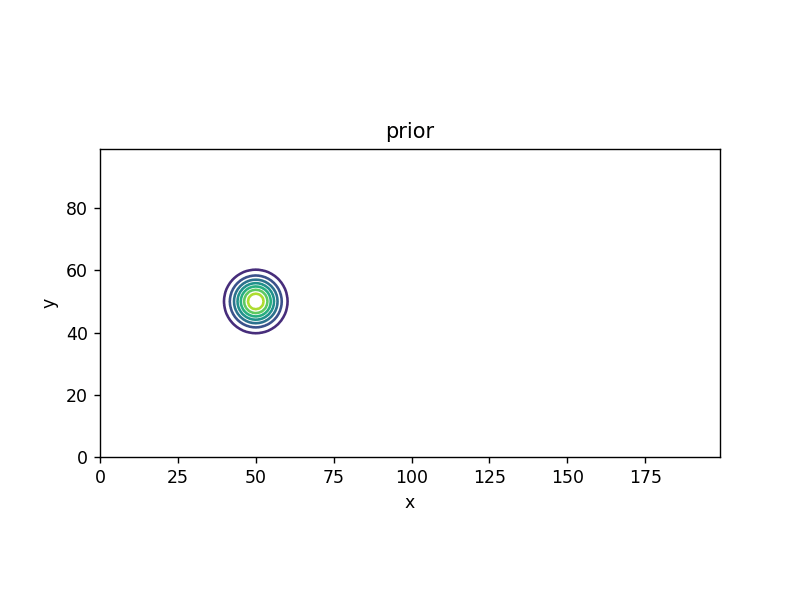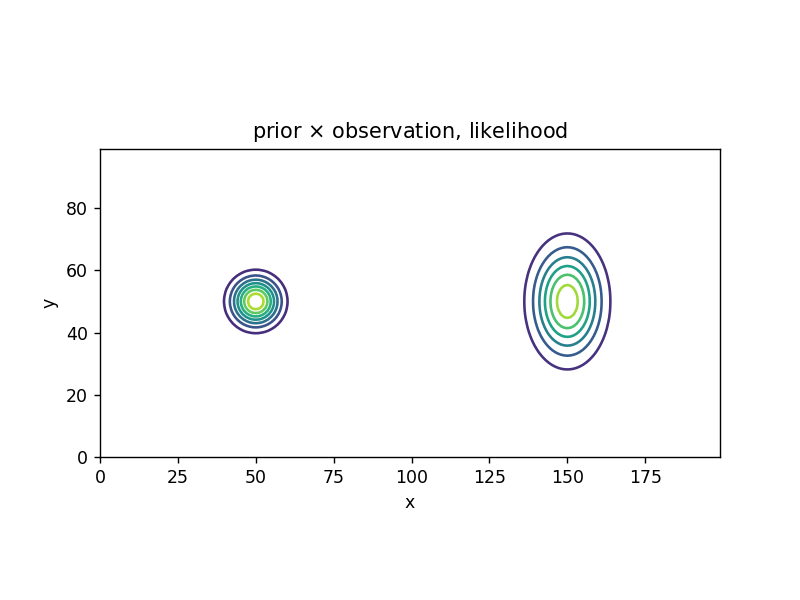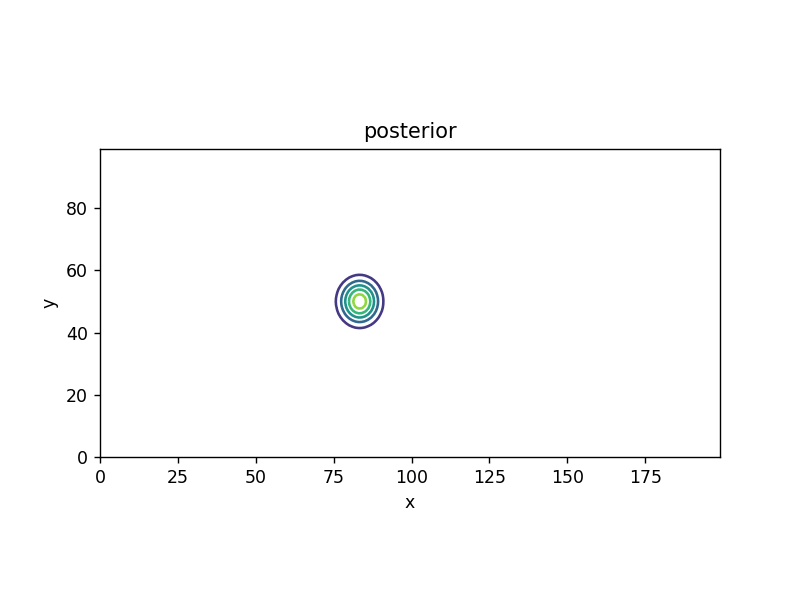
| Python |
|---|
|
(こちらの『sensor_data/』ディレクトリにあるファイルを使わせていただきました)
最小二乗法による最尤推定
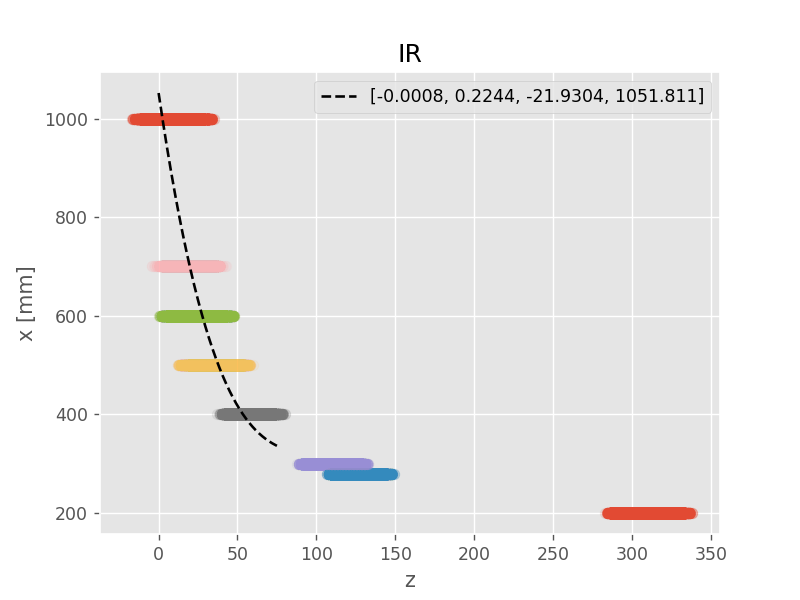 | 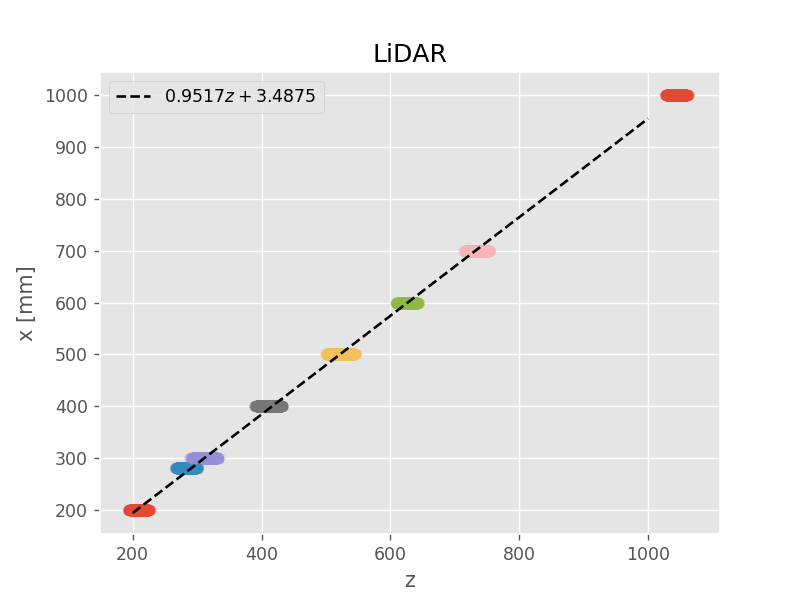 |
破線が最尤推定解(maximum likelihood)
モデル選択(多項式の次数)は手作業による試行錯誤。IR センサーは3次式、LiDAR センサーは1次式に決定。また、IR センサーは(近い距離の実験データが足りなく)上手くモデルが作れなかったため、定義域 \( ( 0 \leq z \leq 75 ) \) を適当に設定
ソースコード
| Python |
|---|
|
(NumPy の polyfit() 関数と poly1d() 関数を利用)
推定結果(\( x_{\mathrm{ML}} \))
| IPython |
|---|
|
© 2020 Tadakazu Nagai